|
Microstate (statistical Mechanics)
In statistical mechanics, a microstate is a specific configuration of a system that describes the precise positions and momenta of all the individual particles or components that make up the system. Each microstate has a certain probability of occurring during the course of the system's thermal fluctuations. In contrast, the macrostate of a system refers to its macroscopic properties, such as its temperature, pressure, volume and density. Treatments on statistical mechanics define a macrostate as follows: a particular set of values of energy, the number of particles, and the volume of an isolated thermodynamic system is said to specify a particular macrostate of it. In this description, microstates appear as different possible ways the system can achieve a particular macrostate. A macrostate is characterized by a probability distribution of possible states across a certain statistical ensemble of all microstates. This distribution describes the probability of finding the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statistics. Each attempts to summarize or typify a given group of data, illustrating the magnitude and sign of the data set. Which of these measures is most illuminating depends on what is being measured, and on context and purpose. The ''arithmetic mean'', also known as "arithmetic average", is the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the numbers are from observing a sample of a larger group, the arithmetic mean is termed the '' sample mean'' (\bar) to distinguish it from the group mean (or expected value) of the underlying distribution, denoted \mu or \mu_x. Outside probability and statistics, a wide rang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Space
The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the phase space usually consists of all possible values of the position and momentum parameters. It is the direct product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. Principles In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase-spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degrees Of Freedom (physics And Chemistry)
In physics and chemistry, a degree of freedom is an independent physical parameter in the chosen parameterization of a physical system. More formally, given a parameterization of a physical system, the number of degrees of freedom is the smallest number n of parameters whose values need to be known in order to always be possible to determine the values of ''all'' parameters in the chosen parameterization. In this case, any set of n such parameters are called degrees of freedom. The location of a particle in three-dimensional space requires three Coordinate system, position coordinates. Similarly, the direction and speed at which a particle moves can be described in terms of three velocity components, each in reference to the three dimensions of space. So, if the time evolution of the system is Deterministic system, deterministic (where the state at one instant uniquely determines its past and future position and velocity as a function of time), such a system has six degrees of f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adiabatic Theorem
The adiabatic theorem is a concept in quantum mechanics. Its original form, due to Max Born and Vladimir Fock (1928), was stated as follows: :''A physical system remains in its instantaneous eigenstate if a given perturbation is acting on it slowly enough and if there is a gap between the eigenvalue and the rest of the Hamiltonian's spectrum.'' In simpler terms, a quantum mechanical system subjected to gradually changing external conditions adapts its functional form, but when subjected to rapidly varying conditions there is insufficient time for the functional form to adapt, so the spatial probability density remains unchanged. Adiabatic pendulum At the 1911 Solvay conference, Einstein gave a lecture on the quantum hypothesis, which states that E = nh \nu for atomic oscillators. After Einstein's lecture, Hendrik Lorentz commented that, classically, if a simple pendulum is shortened by holding the wire between two fingers and sliding down, it seems that its energy will change ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Work (thermodynamics)
Thermodynamic work is one of the principal kinds of process by which a thermodynamic system can interact with and transfer energy to its surroundings. This results in externally measurable macroscopic forces on the system's surroundings, which can cause mechanical work, to lift a weight, for example,Kittel, C. Kroemer, H. (1980). ''Thermal Physics'', second edition, W.H. Freeman, San Francisco, or cause changes in electromagnetic,Guggenheim, E.A. (1985). ''Thermodynamics. An Advanced Treatment for Chemists and Physicists'', seventh edition, North Holland, Amsterdam, .Jackson, J.D. (1975). ''Classical Electrodynamics'', second edition, John Wiley and Sons, New York, .Konopinski, E.J. (1981). ''Electromagnetic Fields and Relativistic Particles'', McGraw-Hill, New York, . or gravitationalNorth, G.R., Erukhimova, T.L. (2009). ''Atmospheric Thermodynamics. Elementary Physics and Chemistry'', Cambridge University Press, Cambridge (UK), . variables. Also, the surroundings can perform t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
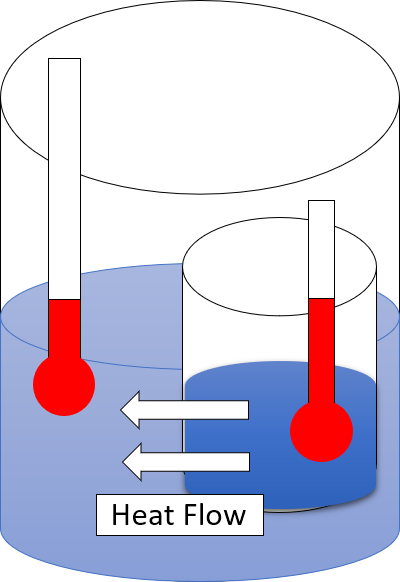
Heat
In thermodynamics, heat is energy in transfer between a thermodynamic system and its surroundings by such mechanisms as thermal conduction, electromagnetic radiation, and friction, which are microscopic in nature, involving sub-atomic, atomic, or molecular particles, or small surface irregularities, as distinct from the macroscopic modes of energy transfer, which are thermodynamic work and transfer of matter. For a closed system (transfer of matter excluded), the heat involved in a process is the difference in internal energy between the final and initial states of a system, after subtracting the work done in the process. For a closed system, this is the formulation of the first law of thermodynamics. Calorimetry is measurement of quantity of energy transferred as heat by its effect on the states of interacting bodies, for example, by the amount of ice melted or by change in temperature of a body. In the International System of Units (SI), the unit of measurement for he ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Third Law Of Thermodynamics
The third law of thermodynamics states that the entropy of a closed system at thermodynamic equilibrium approaches a constant value when its temperature approaches absolute zero. This constant value cannot depend on any other parameters characterizing the system, such as pressure or applied magnetic field. At absolute zero (zero kelvins) the system must be in a state with the minimum possible energy. Entropy is related to the number of accessible microstates, and there is typically one unique state (called the ground state) with minimum energy. In such a case, the entropy at absolute zero will be exactly zero. If the system does not have a well-defined order (if its order is glassy, for example), then there may remain some finite entropy as the system is brought to very low temperatures, either because the system becomes locked into a configuration with non-minimal energy or because the minimum energy state is non-unique. The constant value is called the residual entropy of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second Law Of Thermodynamics
The second law of thermodynamics is a physical law based on Universal (metaphysics), universal empirical observation concerning heat and Energy transformation, energy interconversions. A simple statement of the law is that heat always flows spontaneously from hotter to colder regions of matter (or 'downhill' in terms of the temperature gradient). Another statement is: "Not all heat can be converted into Work (thermodynamics), work in a cyclic process."Young, H. D; Freedman, R. A. (2004). ''University Physics'', 11th edition. Pearson. p. 764. The second law of thermodynamics establishes the concept of entropy as a physical property of a thermodynamic system. It predicts whether processes are forbidden despite obeying the requirement of conservation of energy as expressed in the first law of thermodynamics and provides necessary criteria for spontaneous processes. For example, the first law allows the process of a cup falling off a table and breaking on the floor, as well as allowi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ludwig Boltzmann
Ludwig Eduard Boltzmann ( ; ; 20 February 1844 – 5 September 1906) was an Austrian mathematician and Theoretical physics, theoretical physicist. His greatest achievements were the development of statistical mechanics and the statistical explanation of the second law of thermodynamics. In 1877 he provided the current definition of entropy, S = k_ \ln \Omega, where Ω is the number of microstates whose energy equals the system's energy, interpreted as a measure of the statistical disorder of a system. Max Planck named the constant the Boltzmann constant. Statistical mechanics is one of the pillars of modern physics. It describes how macroscopic observations (such as temperature and pressure) are related to microscopic parameters that fluctuate around an average. It connects thermodynamic quantities (such as heat capacity) to microscopic behavior, whereas, in classical thermodynamics, the only available option would be to measure and tabulate such quantities for various mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Microcanonical Ensemble
In statistical mechanics, the microcanonical ensemble is a statistical ensemble that represents the possible states of a mechanical system whose total energy is exactly specified. The system is assumed to be isolated in the sense that it cannot exchange energy or particles with its environment, so that (by conservation of energy) the energy of the system does not change with time. The primary macroscopic variables of the microcanonical ensemble are the total number of particles in the system (symbol: ), the system's volume (symbol: ), as well as the total energy in the system (symbol: ). Each of these is assumed to be constant in the ensemble. For this reason, the microcanonical ensemble is sometimes called the ensemble. In simple terms, the microcanonical ensemble is defined by assigning an equal probability to every microstate whose energy falls within a range centered at . All other microstates are given a probability of zero. Since the probabilities must add up to 1, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative thermal energy of particles in a ideal gas, gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the molar gas constant, in Planck's law of black-body radiation and Boltzmann's entropy formula, and is used in calculating Johnson–Nyquist noise, thermal noise in resistors. The Boltzmann constant has Dimensional analysis, dimensions of energy divided by temperature, the same as entropy and heat capacity. It is named after the Austrian scientist Ludwig Boltzmann. As part of the 2019 revision of the SI, the Boltzmann constant is one of the seven "Physical constant, defining constants" that have been defined so as to have exact finite decimal values in SI units. They are used in various combinations to define the seven SI base units. The Boltzmann constant is defined to be exactly joules per kelvin, with the effect of defining the SI unit ke ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |