|
Mark Krasnosel'skii
Mark Aleksandrovich Krasnoselsky (; 27 April 1920, Starokostiantyniv – 13 February 1997, Moscow) or Mark Alexsandrovich Krasnoselskii was a Soviet and Russian mathematician renowned for his work on nonlinear functional analysis and its applications. Biography Early years Mark Krasnoselsky was born in Starokostiantyniv, where his father worked as a construction engineer and his mother taught in an elementary school. In 1932 the Krasnoselsky family moved to Berdiansk and in 1938 Mark entered the physico-mathematical faculty of Kyiv University, which was evacuated at the beginning of World War II to Kazakhstan where it became known as the ''Joint Ukrainian University''. He graduated in 1942, in the middle of the war, served four years in the Soviet Army, became Candidate in Science in 1948, with a dissertation on ''self-adjoint extensions of operators with nondense domains'', before getting the title of ''Doctor in Science'' in 1950, with a thesis on investigations in N ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Andronov Prize
The Andronov Prize is a Soviet and Russian mathematics prize, awarded for outstanding works in the classical mechanics and control theory. It is named after the Soviet physicist and member of the Soviet Academy of Sciences Alexander Alexandrovich Andronov. Between 1971 and 1990 the prize was awarded by the USSR Academy of Sciences. It was re-established by the Russian Academy of Sciences The Russian Academy of Sciences (RAS; ''Rossíyskaya akadémiya naúk'') consists of the national academy of Russia; a network of scientific research institutes from across the Russian Federation; and additional scientific and social units such ... in 1993 and was awarded till 2024. It is generally awarded to a single scientist or a team of up to three scientists once every three years. The first prize in 1971 was awarded to Academician of the USSR Academy of Sciences V.V. Petrov for a series of works on control theory and the principles of constructing nonlinear systems and servomechanisms, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nemytskii Operator
In mathematics, Nemytskii operators are a class of nonlinear operators on Lp space, ''L''''p'' spaces with good continuous function, continuity and bounded function, boundedness properties. They take their name from the mathematician Viktor Vladimirovich Nemytskii. General definition of Superposition operator Let \mathbb,\ \mathbb,\ \mathbb \neq \varnothing be non-empty sets, then \mathbb^ \mathbb,\ \mathbb^\mathbb — sets of mappings from \mathbb with values in \mathbb and \mathbb respectively. The Nemytskii superposition operator H\ \colon \mathbb^\mathbb \to \mathbb^\mathbb is the mapping induced by the function h\ \colon \mathbb \times \mathbb \to \mathbb, and such that for any function \varphi \in \mathbb^\mathbb its image is given by the rule (H\varphi)(x) = h(x, \varphi(x)) \in \mathbb, \quad \mbox\ x\in \mathbb. The function h is called the generator of the Nemytskii operator H. Definition of Nemytskii operator Let Ω be a domain (an open set, open and connected spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Operator
An integral operator is an operator that involves integration. Special instances are: * The operator of integration itself, denoted by the integral symbol * Integral linear operators, which are linear operators induced by bilinear forms involving integrals * Integral transforms, which are maps between two function space In mathematics, a function space is a set of functions between two fixed sets. Often, the domain and/or codomain will have additional structure which is inherited by the function space. For example, the set of functions from any set into a ve ...s, which involve integrals {{Authority control Integral calculus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives. The function is often thought of as an "unknown" that solves the equation, similar to how is thought of as an unknown number solving, e.g., an algebraic equation like . However, it is usually impossible to write down explicit formulae for solutions of partial differential equations. There is correspondingly a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity and stability. Among the many open questions are the existence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-adjoint Operator
In mathematics, a self-adjoint operator on a complex vector space ''V'' with inner product \langle\cdot,\cdot\rangle is a linear map ''A'' (from ''V'' to itself) that is its own adjoint. That is, \langle Ax,y \rangle = \langle x,Ay \rangle for all x, y ∊ ''V''. If ''V'' is finite-dimensional with a given orthonormal basis, this is equivalent to the condition that the matrix of ''A'' is a Hermitian matrix, i.e., equal to its conjugate transpose ''A''. By the finite-dimensional spectral theorem, ''V'' has an orthonormal basis such that the matrix of ''A'' relative to this basis is a diagonal matrix with entries in the real numbers. This article deals with applying generalizations of this concept to operators on Hilbert spaces of arbitrary dimension. Self-adjoint operators are used in functional analysis and quantum mechanics. In quantum mechanics their importance lies in the Dirac–von Neumann formulation of quantum mechanics, in which physical observables such as position, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
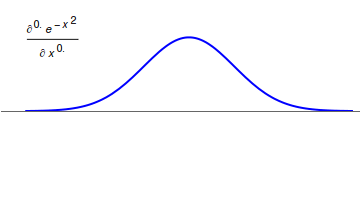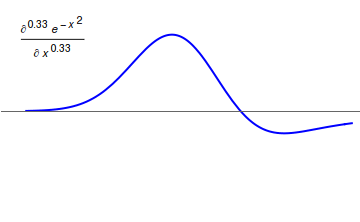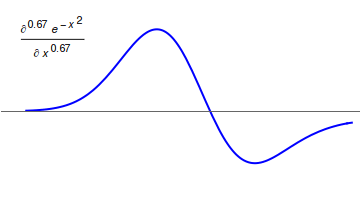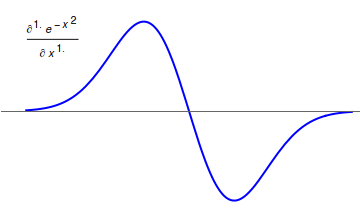
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar glyphs, such as identities. J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function that is, repeatedly composing D with itself, as in \begin D^n(f) &= (\underbrace_n)(f) \\ &= \underbrace_n (f)\cdots))). \end For example, one may ask for a meaningful interpretation of \sqrt = D^ as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied to any f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Theory
Control theory is a field of control engineering and applied mathematics that deals with the control system, control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any ''delay'', ''overshoot'', or ''steady-state error'' and ensuring a level of control Stability theory, stability; often with the aim to achieve a degree of Optimal control, optimality. To do this, a controller with the requisite corrective behavior is required. This controller monitors the controlled process variable (PV), and compares it with the reference or Setpoint (control system), set point (SP). The difference between actual and desired value of the process variable, called the ''error'' signal, or SP-PV error, is applied as feedback to generate a control action to bring the controlled process variable to the same value as the set point. Other aspects ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Engineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, systems. Modern engineering comprises many subfields which include designing and improving infrastructure, machinery, vehicles, electronics, Materials engineering, materials, and energy systems. The Academic discipline, discipline of engineering encompasses a broad range of more Academic specialization, specialized fields of engineering, each with a more specific emphasis for applications of applied mathematics, mathematics and applied science, science. See glossary of engineering. The word '':wikt:engineering, engineering'' is derived from the Latin . Definition The American Engineers' Council for Professional Development (the predecessor of the Accreditation Board for Engineering and Technology aka ABET) has defined "engineering" as: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanics
Mechanics () is the area of physics concerned with the relationships between force, matter, and motion among Physical object, physical objects. Forces applied to objects may result in Displacement (vector), displacements, which are changes of an object's position relative to its environment. Theoretical expositions of this branch of physics has its origins in Ancient Greece, for instance, in the writings of Aristotle and Archimedes (see History of classical mechanics and Timeline of classical mechanics). During the early modern period, scientists such as Galileo Galilei, Johannes Kepler, Christiaan Huygens, and Isaac Newton laid the foundation for what is now known as classical mechanics. As a branch of classical physics, mechanics deals with bodies that are either at rest or are moving with velocities significantly less than the speed of light. It can also be defined as the physical science that deals with the motion of and forces on bodies not in the quantum realm. History ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Equation
In mathematics, a functional equation is, in the broadest meaning, an equation in which one or several functions appear as unknowns. So, differential equations and integral equations are functional equations. However, a more restricted meaning is often used, where a ''functional equation'' is an equation that relates several values of the same function. For example, the logarithm functions are essentially characterized by the ''logarithmic functional equation'' \log(xy)=\log(x) + \log(y). If the domain of the unknown function is supposed to be the natural numbers, the function is generally viewed as a sequence, and, in this case, a functional equation (in the narrower meaning) is called a recurrence relation. Thus the term ''functional equation'' is used mainly for real functions and complex functions. Moreover a smoothness condition is often assumed for the solutions, since without such a condition, most functional equations have very irregular solutions. For example, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |