|
Madhava's Value Of π
Madhava's correction term is a mathematical expression attributed to Madhava of Sangamagrama (c. 1340 – c. 1425), the founder of the Kerala school of astronomy and mathematics, that can be used to give a better approximation to the value of the mathematical constant (''pi'') than the partial sum approximation obtained by truncating the Madhava–Leibniz infinite series for . The Madhava–Leibniz infinite series for is :\frac=1-\frac+\frac-\frac+ \cdots Taking the partial sum of the first n terms we have the following approximation to : :\frac \approx 1-\frac+\frac-\frac+ \cdots + (-1)^\frac Denoting the Madhava correction term by F(n), we have the following better approximation to : :\frac \approx 1-\frac+\frac-\frac+ \cdots + (-1)^\frac + (-1)^n F(n) Three different expressions have been attributed to Madhava as possible values of F(n), namely, :F_1(n)=\frac :F_2(n)=\frac :F_3(n)=\frac In the extant writings of the mathematicians of the Kerala school there are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Madhava Of Sangamagrama
Mādhava of Sangamagrāma (Mādhavan) Availabl/ref> () was an Indian mathematician and astronomer who is considered to be the founder of the Kerala school of astronomy and mathematics in the Late Middle Ages. Madhava made pioneering contributions to the study of infinite series, calculus, trigonometry, geometry and algebra. He was the first to use infinite series approximations for a range of trigonometric functions, which has been called the "decisive step onward from the finite procedures of ancient mathematics to treat their limit-passage to infinity". Biography Little is known about Madhava's life with certainty. However, from scattered references to Madhava found in diverse manuscripts, historians of Kerala school have pieced together information about the mathematician. In a manuscript preserved in the Oriental Institute, Baroda, Madhava has been referred to as ''Mādhavan vēṇvārōhādīnām karttā ... Mādhavan Ilaññippaḷḷi Emprān''. It has been noted that th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kerala School Of Astronomy And Mathematics
The Kerala school of astronomy and mathematics or the Kerala school was a school of Indian mathematics, mathematics and Indian astronomy, astronomy founded by Madhava of Sangamagrama in Kingdom of Tanur, Tirur, Malappuram district, Malappuram, Kerala, India, which included among its members: Parameshvara, Neelakanta Somayaji, Jyeshtadeva, Achyuta Pisharati, Melpathur Narayana Bhattathiri and Achyuta Panikkar. The school flourished between the 14th and 16th centuries and its original discoveries seem to have ended with Melpathur Narayana Bhattathiri, Narayana Bhattathiri (1559–1632). In attempting to solve astronomical problems, the Kerala school independently discovered a number of important mathematical concepts. Their most important results—series expansion for trigonometric functions—were described in Sanskrit verse in a book by Neelakanta called ''Tantrasangraha'' (around 1500), and again in a commentary on this work, called ''Tantrasangraha-vakhya'', of unknown authors ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Madhava Series
In mathematics, a Madhava series is one of the three Taylor series expansions for the sine, cosine, and arctangent function (mathematics), functions discovered in 14th or 15th century in Kerala, India by the mathematician and astronomer Madhava of Sangamagrama (c. 1350 – c. 1425) or his followers in the Kerala school of astronomy and mathematics. Using modern notation, these series are: :\begin \sin \theta &= \theta - \frac + \frac - \frac + \cdots &&= \sum_^\infty \frac\theta^, \\[10mu] \cos \theta &= 1 - \frac + \frac - \frac + \cdots &&= \sum_^\infty \frac\theta^, \\[10mu] \arctan x &= x - \frac + \frac - \frac + \cdots &&= \sum_^\infty \fracx^ \quad \text , x, \leq 1. \end All three series were later independently discovered in 17th century Europe. The series for sine and cosine were rediscovered by Isaac Newton in 1669, and the series for arctangent was rediscovered by James Gregory (mathematician), James Gregory in 1671 and Gottfried Wilhelm Leibniz, Gottfried ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tantrasangraha
Tantrasamgraha, or Tantrasangraha, (literally, ''A Compilation of the System'') is an important astronomical treatise written by Nilakantha Somayaji, an astronomer/mathematician belonging to the Kerala school of astronomy and mathematics. The treatise was completed in 1501 CE. It consists of 432 verses in Sanskrit divided into eight chapters. Tantrasamgraha had spawned a few commentaries: ''Tantrasamgraha-vyakhya'' of anonymous authorship and ''Yuktibhāṣā'' authored by Jyeshtadeva in about 1550 CE. Tantrasangraha, together with its commentaries, bring forth the depths of the mathematical accomplishments the Kerala school of astronomy and mathematics, in particular the achievements of the remarkable mathematician of the school Sangamagrama Madhava. In his ''Tantrasangraha'', Nilakantha revised Aryabhata's model for the planets Mercury and Venus. According to George G Joseph his equation of the centre for these planets remained the most accurate until the time of Johannes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nilakantha Somayaji
Keļallur Nīlakaṇṭha Somayāji (14 June 1444 – 1544), also referred to as Keļallur Comatiri, was a mathematician and astronomer of the Kerala school of astronomy and mathematics. One of his most influential works was the comprehensive astronomical treatise '' Tantrasamgraha'' completed in 1501. He had also composed an elaborate commentary on Aryabhatiya called the ''Aryabhatiya Bhasya''. In this Bhasya, Nilakantha had discussed infinite series expansions of trigonometric functions and problems of algebra and spherical geometry. ''Grahapariksakrama'' is a manual on making observations in astronomy based on instruments of the time. Early life Nilakantha was born into a Brahmin family which came from South Malabar in Kerala. Biographical details Nilakantha Somayaji was one of the very few authors of the scholarly traditions of India who had cared to record details about his own life and times. In one of his works titled '' Siddhanta-star'' and also in his ow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Madhava Correction Terms 1 And 2
Mādhava means Krishna. It may also refer to: *a Sanskrit patronymic, "descendant of Madhu (a man of the Yadu tribe)". ** especially of Krishna, see Madhava (Vishnu) *** an icon of Krishna ** Madhava of Sangamagrama, fourteenth-century Indian mathematician ** Madhvacharya, philosopher in the Vaishnavism tradition ** Madhava Vidyaranya, Advaita saint and brother of Sayana ** Venkata Madhava, 10th to 12th century commentator of the Rigveda ** Madhavdeva, 16th-century proponent of Ekasarana dharma, neo-Vaishnavism of Assam *relating to springtime; the first month of spring, see Chaitra *Madhava or Madhava-kara, an Indian physician of the 7th or early 8th century *Madhava, titular protagonist of the ancient Indian drama Mālatīmādhava by Bhavabhuti *Madhava, a character in the 11th-century Indian story collection ''Shringara-manjari-katha'' See also * * *Madhavan (other) * Madhavi (other) * Madhab (other) *Madhavaram (other) * ''Madhav'' (film), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continued Fraction
A continued fraction is a mathematical expression that can be written as a fraction with a denominator that is a sum that contains another simple or continued fraction. Depending on whether this iteration terminates with a simple fraction or not, the continued fraction is finite or infinite. Different fields of mathematics have different terminology and notation for continued fraction. In number theory the standard unqualified use of the term continued fraction refers to the special case where all numerators are 1, and is treated in the article simple continued fraction. The present article treats the case where numerators and denominators are sequences \,\ of constants or functions. From the perspective of number theory, these are called generalized continued fraction. From the perspective of complex analysis or numerical analysis, however, they are just standard, and in the present article they will simply be called "continued fraction". Formulation A continued fraction is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Algorithm
In mathematics, the Euclidean algorithm,Some widely used textbooks, such as I. N. Herstein's ''Topics in Algebra'' and Serge Lang's ''Algebra'', use the term "Euclidean algorithm" to refer to Euclidean division or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his ''Elements'' (). It is an example of an ''algorithm'', a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
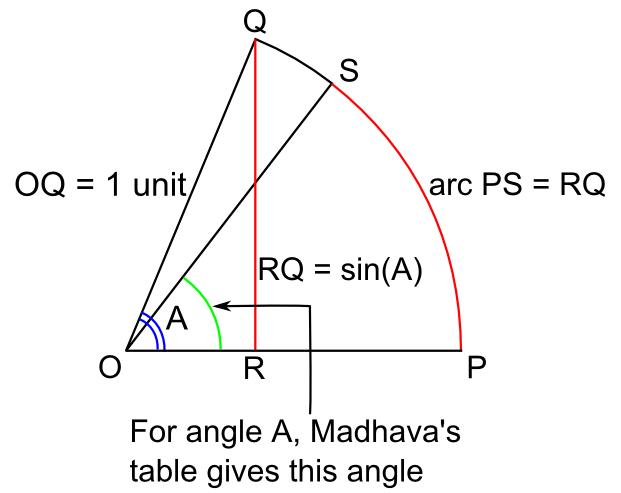
Madhava's Sine Table
Madhava's sine table is the table of trigonometric sines constructed by the 14th century Kerala mathematician-astronomer Madhava of Sangamagrama (c. 1340 – c. 1425). The table lists the jya-s or Rsines of the twenty-four angles from 3.75 ° to 90° in steps of 3.75° (1/24 of a right angle, 90°). Rsine is just the sine multiplied by a selected radius and given as an integer. In this table, as in Aryabhata's earlier table, ''R'' is taken as 21600 ÷ 2 ≈ 3437.75. The table is encoded in the letters of the Sanskrit alphabet using the Katapayadi system, giving entries the appearance of the verses of a poem. Madhava's original work containing the table has not been found. The table is reproduced in the ''Aryabhatiyabhashya'' of Nilakantha Somayaji''The Aryabhatiam of Aryabhattacharya with the Bhashya of Nilakantha Somasutvan, Part 1 - Gaṇitapāda,'' Edited by K. Sambasiva Sastri, Trivandrum Sanskrit Series No.101. p. 55. https://archive.org/details/Triva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
History Of Calculus
Calculus, originally called infinitesimal calculus, is a mathematical discipline focused on limits, continuity, derivatives, integrals, and infinite series. Many elements of calculus appeared in ancient Greece, then in China and the Middle East, and still later again in medieval Europe and in India. Infinitesimal calculus was developed in the late 17th century by Isaac Newton and Gottfried Wilhelm Leibniz independently of each other. An argument over priority led to the Leibniz–Newton calculus controversy which continued until the death of Leibniz in 1716. The development of calculus and its uses within the sciences have continued to the present. Etymology In mathematics education, ''calculus'' denotes courses of elementary mathematical analysis, which are mainly devoted to the study of functions and limits. The word ''calculus'' is Latin for "small pebble" (the diminutive of '' calx,'' meaning "stone"), a meaning which still persists in medicine. Because such pebbles were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |