|
Logical Possibility
Logical possibility refers to a logical proposition that cannot be disproved, using the axioms and rules of a given system of logic. The logical possibility of a proposition will depend upon the system of logic being considered, rather than on the violation of any single rule. Some systems of logic restrict inferences from inconsistent propositions or even allow for true contradictions. Other logical systems have more than two truth-values instead of a binary of such values. However, when talking about logical possibility, it is often assumed that the system in question is classical propositional logic. Similarly, the criterion for logical possibility is often based on whether or not a proposition is contradictory and as such, is often thought of as the broadest type of possibility. In modal logic, a logical proposition is possible if it is true in some possible world. The universe of "possible worlds" depends upon the axioms and rules of the logical system in which one is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Proposition
In logic and linguistics, a proposition is the meaning of a declarative sentence. In philosophy, " meaning" is understood to be a non-linguistic entity which is shared by all sentences with the same meaning. Equivalently, a proposition is the non-linguistic bearer of truth or falsity which makes any sentence that expresses it either true or false. While the term "proposition" may sometimes be used in everyday language to refer to a linguistic statement which can be either true or false, the technical philosophical term, which differs from the mathematical usage, refers exclusively to the non-linguistic meaning behind the statement. The term is often used very broadly and can also refer to various related concepts, both in the history of philosophy and in contemporary analytic philosophy. It can generally be used to refer to some or all of the following: The primary bearers of truth values (such as "true" and "false"); the objects of belief and other propositional attitudes (i.e. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
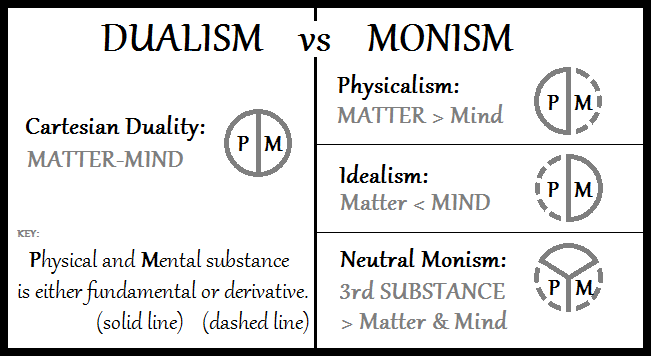
Metaphysics
Metaphysics is the branch of philosophy that studies the fundamental nature of reality, the first principles of being, identity and change, space and time, causality, necessity, and possibility. It includes questions about the nature of consciousness and the relationship between mind and matter, between Substance theory, substance and Property (philosophy), attribute, and between potentiality and actuality. The word "metaphysics" comes from two Greek words that, together, literally mean "after or behind or among [the study of] the natural". It has been suggested that the term might have been coined by a first century CE editor who assembled various small selections of Aristotle's works into the treatise we now know by the name Metaphysics (Aristotle), ''Metaphysics'' (μετὰ τὰ φυσικά, ''meta ta physika'', 'after the Physics (Aristotle), ''Physics'' ', another of Aristotle's works). Metaphysics studies questions related to what it is for something to exist an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Possible World
A possible world is a complete and consistent way the world is or could have been. Possible worlds are widely used as a formal device in logic, philosophy, and linguistics in order to provide a semantics for intensional and modal logic. Their metaphysical status has been a subject of controversy in philosophy, with modal realists such as David Lewis arguing that they are literally existing alternate realities, and others such as Robert Stalnaker arguing that they are not. Logic Possible worlds are one of the foundational concepts in modal and intensional logics. Formulas in these logics are used to represent statements about what ''might'' be true, what ''should'' be true, what one ''believes'' to be true and so forth. To give these statements a formal interpretation, logicians use structures containing possible worlds. For instance, in the relational semantics for classical propositional modal logic, the formula \Diamond P (read as "possibly P") is actually true if and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Possibility Theory
Possibility theory is a mathematical theory for dealing with certain types of uncertainty and is an alternative to probability theory. It uses measures of possibility and necessity between 0 and 1, ranging from impossible to possible and unnecessary to necessary, respectively. Professor Lotfi Zadeh first introduced possibility theory in 1978 as an extension of his theory of fuzzy sets and fuzzy logic. Didier Dubois and Henri Prade further contributed to its development. Earlier in the 1950s, economist G. L. S. Shackle proposed the min/max algebra to describe degrees of potential surprise. Formalization of possibility For simplicity, assume that the universe of discourse Ω is a finite set. A possibility measure is a function \operatorname from 2^\Omega to , 1such that: :Axiom 1: \operatorname(\varnothing) = 0 :Axiom 2: \operatorname(\Omega) = 1 :Axiom 3: \operatorname(U \cup V) = \max \left( \operatorname(U), \operatorname(V) \right) for any disjoint subsets U and V. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paradox
A paradox is a logically self-contradictory statement or a statement that runs contrary to one's expectation. It is a statement that, despite apparently valid reasoning from true premises, leads to a seemingly self-contradictory or a logically unacceptable conclusion. A paradox usually involves contradictory-yet-interrelated elements that exist simultaneously and persist over time. They result in "persistent contradiction between interdependent elements" leading to a lasting "unity of opposites". In logic, many paradoxes exist that are known to be invalid arguments, yet are nevertheless valuable in promoting critical thinking, while other paradoxes have revealed errors in definitions that were assumed to be rigorous, and have caused axioms of mathematics and logic to be re-examined. One example is Russell's paradox, which questions whether a "list of all lists that do not contain themselves" would include itself, and showed that attempts to found set theory on the identificatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modal Logic
Modal logic is a collection of formal systems developed to represent statements about necessity and possibility. It plays a major role in philosophy of language, epistemology, metaphysics, and natural language semantics. Modal logics extend other systems by adding unary operators \Diamond and \Box, representing possibility and necessity respectively. For instance the modal formula \Diamond P can be read as "possibly P" while \Box P can be read as "necessarily P". Modal logics can be used to represent different phenomena depending on what kind of necessity and possibility is under consideration. When \Box is used to represent epistemic necessity, \Box P states that P is epistemically necessary, or in other words that it is known. When \Box is used to represent deontic necessity, \Box P states that P is a moral or legal obligation. In the standard relational semantics for modal logic, formulas are assigned truth values relative to a '' possible world''. A formula's truth value ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rigid Designator
In modal logic and the philosophy of language, a term is said to be a rigid designator or absolute substantial term when it designates (picks out, denotes, refers to) the same thing in ''all possible worlds'' in which that thing exists. A designator is ''persistently rigid'' if it also designates nothing in all other possible worlds. A designator is ''obstinately rigid'' if it designates the same thing in every possible world, period, whether or not that thing exists in that world. Rigid designators are contrasted with ''connotative terms'', ''non-rigid'' or ''flaccid designators'', which may designate different things in different possible worlds. History The Scholastic philosophers in the Middle Ages developed a theory of properties of terms in which different classifications of concepts feature prominently. Concepts, and the terms that signify them, can be divided into absolute or connotative, according to the mode in which they signify. If they signify something absolutely, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
A Posteriori Necessity
''A posteriori'' necessity is a thesis in metaphysics and the philosophy of language, that some statements of which we must acquire knowledge a posteriori are also necessarily true. It challenges previously widespread belief that only ''a priori'' knowledge can be necessary. It draws on a number of philosophical concepts such as necessity, the causal theory of reference, rigidity, and the a priori a posteriori distinction. It was first introduced by philosopher Saul Kripke in his 1970 series of lectures at Princeton University. The transcript of these lectures was then compiled and assembled into his seminal book, '' Naming and Necessity''. Main argument for a posteriori necessity Here is an overview of the argument: :(P1) 'Hesperus' is a proper name that refers to the evening star. 'Phosphorus' is also a proper name and it refers to the morning star. But the evening star and the morning star are the same planetary body (Venus). So both names designate Venus. :(P2) If bo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Saul Kripke
Saul Aaron Kripke (; November 13, 1940 – September 15, 2022) was an American philosopher and logician in the analytic tradition. He was a Distinguished Professor of Philosophy at the Graduate Center of the City University of New York and emeritus professor at Princeton University. Since the 1960s, Kripke has been a central figure in a number of fields related to mathematical logic, modal logic, philosophy of language, philosophy of mathematics, metaphysics, epistemology, and recursion theory. Much of his work remains unpublished or exists only as tape recordings and privately circulated manuscripts. Kripke made influential and original contributions to logic, especially modal logic. His principal contribution is a semantics for modal logic involving possible worlds, now called Kripke semantics. He received the 2001 Schock Prize in Logic and Philosophy. Kripke was also partly responsible for the revival of metaphysics after the decline of logical positivism, claimi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stanford Encyclopedia Of Philosophy
The ''Stanford Encyclopedia of Philosophy'' (''SEP'') combines an online encyclopedia of philosophy with peer-reviewed publication of original papers in philosophy, freely accessible to Internet users. It is maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from many academic institutions worldwide. Authors contributing to the encyclopedia give Stanford University the permission to publish the articles, but retain the copyright to those articles. Approach and history As of August 5th, 2022, the ''SEP'' has 1,774 published entries. Apart from its online status, the encyclopedia uses the traditional academic approach of most encyclopedias and academic journals to achieve quality by means of specialist authors selected by an editor or an editorial committee that is competent (although not necessarily considered specialists) in the field covered by the encyclopedia and peer review. The encyclopedia was created ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paraconsistent Logic
A paraconsistent logic is an attempt at a logical system to deal with contradictions in a discriminating way. Alternatively, paraconsistent logic is the subfield of logic that is concerned with studying and developing "inconsistency-tolerant" systems of logic which reject the principle of explosion. Inconsistency-tolerant logics have been discussed since at least 1910 (and arguably much earlier, for example in the writings of Aristotle); however, the term ''paraconsistent'' ("beside the consistent") was first coined in 1976, by the Peruvian philosopher Francisco Miró Quesada Cantuarias. The study of paraconsistent logic has been dubbed paraconsistency, which encompasses the school of dialetheism. Definition In classical logic (as well as intuitionistic logic and most other logics), contradictions entail everything. This feature, known as the principle of explosion or ''ex contradictione sequitur quodlibet'' (Latin, "from a contradiction, anything follows") can be expressed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Consistency
In classical deductive logic, a consistent theory is one that does not lead to a logical contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if it has a model, i.e., there exists an interpretation under which all formulas in the theory are true. This is the sense used in traditional Aristotelian logic, although in contemporary mathematical logic the term ''satisfiable'' is used instead. The syntactic definition states a theory T is consistent if there is no formula \varphi such that both \varphi and its negation \lnot\varphi are elements of the set of consequences of T. Let A be a set of closed sentences (informally "axioms") and \langle A\rangle the set of closed sentences provable from A under some (specified, possibly implicitly) formal deductive system. The set of axioms A is consistent when \varphi, \lnot \varphi \in \langle A \rangle for no formula \varphi. If there exis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |