|
Loss Functions For Classification
In machine learning and mathematical optimization, loss functions for classification are computationally feasible loss functions representing the price paid for inaccuracy of predictions in classification problems (problems of identifying which category a particular observation belongs to). Given \mathcal as the space of all possible inputs (usually \mathcal \subset \mathbb^d), and \mathcal = \ as the set of labels (possible outputs), a typical goal of classification algorithms is to find a function f: \mathcal \to \mathcal which best predicts a label y for a given input \vec. However, because of incomplete information, noise in the measurement, or probabilistic components in the underlying process, it is possible for the same \vec to generate different y. As a result, the goal of the learning problem is to minimize expected loss (also known as the risk), defined as :I = \displaystyle \int_ V(f(\vec),y) \, p(\vec,y) \, d\vec \, dy where V(f(\vec),y) is a given loss function, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tikhonov Regularization
Ridge regression (also known as Tikhonov regularization, named for Andrey Tikhonov) is a method of estimating the coefficients of multiple- regression models in scenarios where the independent variables are highly correlated. It has been used in many fields including econometrics, chemistry, and engineering. It is a method of regularization of ill-posed problems. It is particularly useful to mitigate the problem of multicollinearity in linear regression, which commonly occurs in models with large numbers of parameters. In general, the method provides improved efficiency in parameter estimation problems in exchange for a tolerable amount of bias (see bias–variance tradeoff). The theory was first introduced by Hoerl and Kennard in 1970 in their ''Technometrics'' papers "Ridge regressions: biased estimation of nonorthogonal problems" and "Ridge regressions: applications in nonorthogonal problems". Ridge regression was developed as a possible solution to the imprecision of least s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiable Programming
Differentiable programming is a programming paradigm in which a numeric computer program can be differentiated throughout via automatic differentiation. This allows for gradient-based optimization of parameters in the program, often via gradient descent, as well as other learning approaches that are based on higher-order derivative information. Differentiable programming has found use in a wide variety of areas, particularly scientific computing and machine learning. One of the early proposals to adopt such a framework in a systematic fashion to improve upon learning algorithms was made by the Advanced Concepts Team at the European Space Agency in early 2016. Approaches Most differentiable programming frameworks work by constructing a graph containing the control flow and data structures in the program. Attempts generally fall into two groups: * Static, compiled graph-based approaches such as TensorFlow,TensorFlow 1 uses the static graph approach, whereas TensorFlow 2 uses the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Programming
Quadratic programming (QP) is the process of solving certain mathematical optimization problems involving quadratic functions. Specifically, one seeks to optimize (minimize or maximize) a multivariate quadratic function subject to linear constraints on the variables. Quadratic programming is a type of nonlinear programming. "Programming" in this context refers to a formal procedure for solving mathematical problems. This usage dates to the 1940s and is not specifically tied to the more recent notion of "computer programming." To avoid confusion, some practitioners prefer the term "optimization" — e.g., "quadratic optimization." Problem formulation The quadratic programming problem with variables and constraints can be formulated as follows. Given: * a real-valued, -dimensional vector , * an -dimensional real symmetric matrix , * an -dimensional real matrix , and * an -dimensional real vector , the objective of quadratic programming is to find an -dimensional vector , that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subgradient Method
Subgradient methods are convex optimization methods which use subderivatives. Originally developed by Naum Z. Shor and others in the 1960s and 1970s, subgradient methods are convergent when applied even to a non-differentiable objective function. When the objective function is differentiable, sub-gradient methods for unconstrained problems use the same search direction as the method of gradient descent. Subgradient methods are slower than Newton's method when applied to minimize twice continuously differentiable convex functions. However, Newton's method fails to converge on problems that have non-differentiable kinks. In recent years, some interior-point methods have been suggested for convex minimization problems, but subgradient projection methods and related bundle methods of descent remain competitive. For convex minimization problems with very large number of dimensions, subgradient-projection methods are suitable, because they require little storage. Subgradient project ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
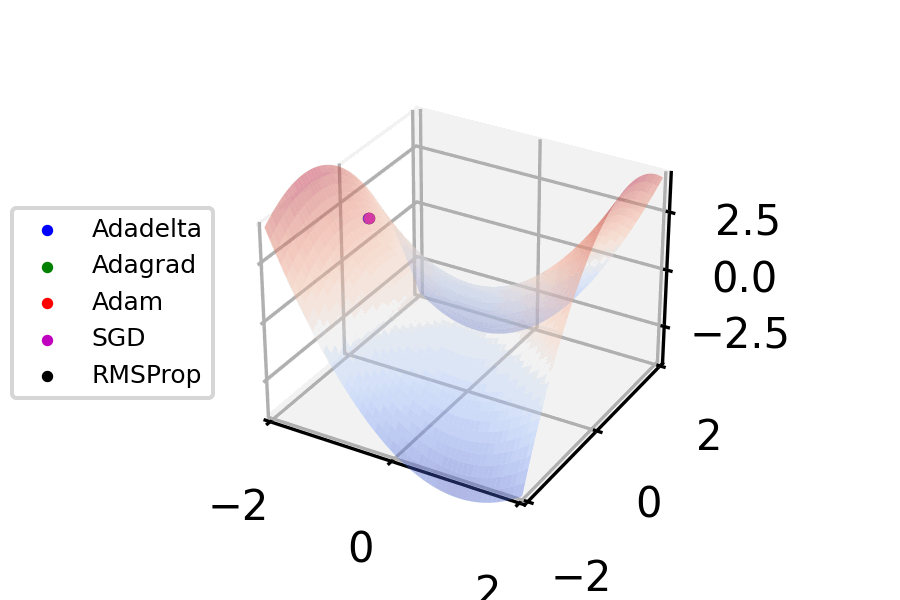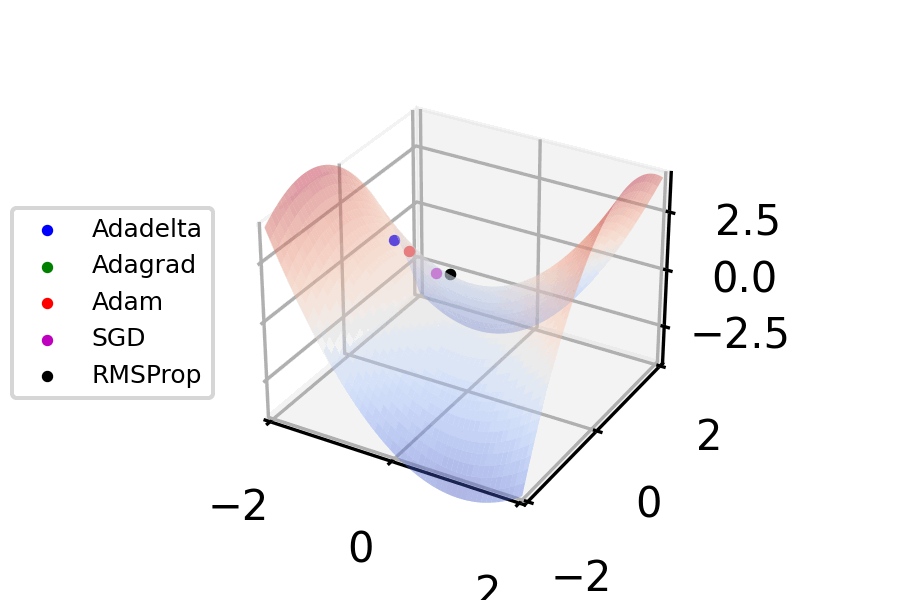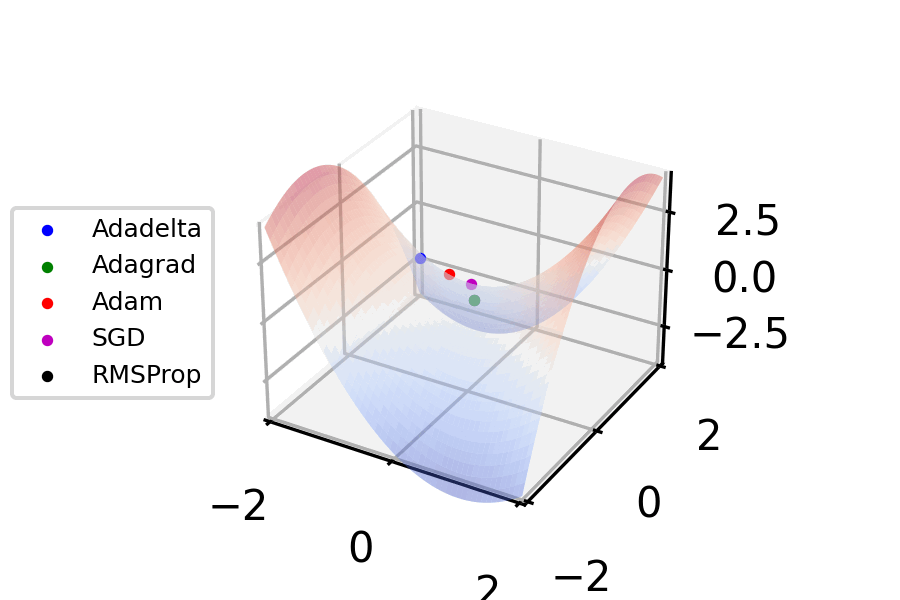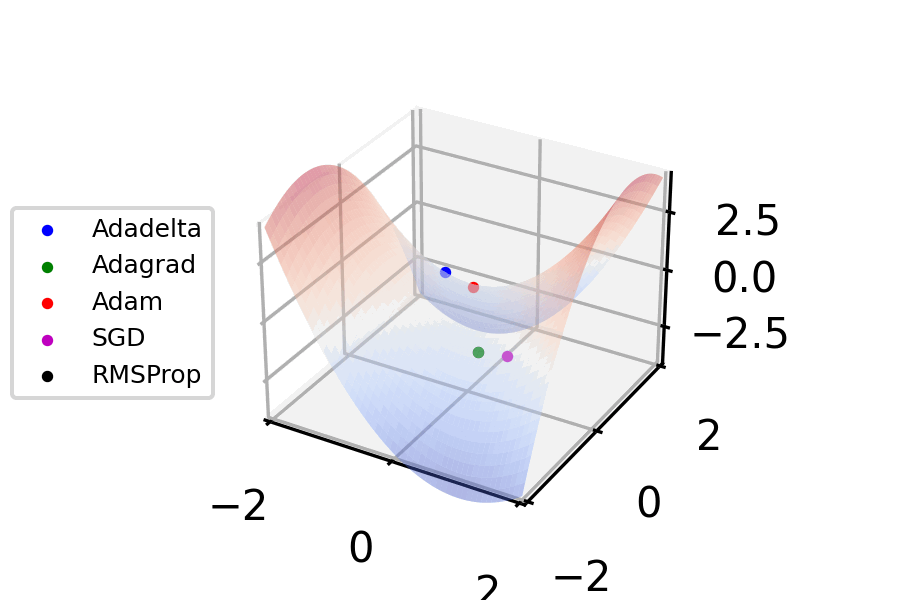
Stochastic Gradient Descent
Stochastic gradient descent (often abbreviated SGD) is an Iterative method, iterative method for optimizing an objective function with suitable smoothness properties (e.g. Differentiable function, differentiable or Subderivative, subdifferentiable). It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient (calculated from the entire data set) by an estimate thereof (calculated from a randomly selected subset of the data). Especially in high-dimensional optimization problems this reduces the very high Computational complexity, computational burden, achieving faster iterations in exchange for a lower Rate of convergence, convergence rate. The basic idea behind stochastic approximation can be traced back to the Robbins–Monro algorithm of the 1950s. Today, stochastic gradient descent has become an important optimization method in machine learning. Background Both statistics, statistical M-estimation, estimation and ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient Descent
Gradient descent is a method for unconstrained mathematical optimization. It is a first-order iterative algorithm for minimizing a differentiable multivariate function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a trajectory that maximizes that function; the procedure is then known as ''gradient ascent''. It is particularly useful in machine learning for minimizing the cost or loss function. Gradient descent should not be confused with local search algorithms, although both are iterative methods for optimization. Gradient descent is generally attributed to Augustin-Louis Cauchy, who first suggested it in 1847. Jacques Hadamard independently proposed a similar method in 1907. Its convergence properties for non-linear optimization problems were first studied by Has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Support Vector Machines
In machine learning, support vector machines (SVMs, also support vector networks) are supervised max-margin models with associated learning algorithms that analyze data for classification and regression analysis. Developed at AT&T Bell Laboratories, SVMs are one of the most studied models, being based on statistical learning frameworks of VC theory proposed by Vapnik (1982, 1995) and Chervonenkis (1974). In addition to performing linear classification, SVMs can efficiently perform non-linear classification using the ''kernel trick'', representing the data only through a set of pairwise similarity comparisons between the original data points using a kernel function, which transforms them into coordinates in a higher-dimensional feature space. Thus, SVMs use the kernel trick to implicitly map their inputs into high-dimensional feature spaces, where linear classification can be performed. Being max-margin models, SVMs are resilient to noisy data (e.g., misclassified examples). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive Part
In mathematics, the positive part of a real or extended real-valued function is defined by the formula f^+(x) = \max(f(x),0) = \begin f(x) & \text f(x) > 0 \\ 0 & \text \end Intuitively, the graph of f^+ is obtained by taking the graph of f, 'chopping off' the part under the -axis, and letting f^+ take the value zero there. Similarly, the negative part of is defined as f^-(x) = \max(-f(x),0) = -\min(f(x),0) = \begin -f(x) & \text f(x) >0 \\ f^- &= - <0. \end One may define the positive and negative part of any function with values in a . The unit is the positive part of the |
AdaBoost
AdaBoost (short for Adaptive Boosting) is a statistical classification meta-algorithm formulated by Yoav Freund and Robert Schapire in 1995, who won the 2003 Gödel Prize for their work. It can be used in conjunction with many types of learning algorithm to improve performance. The output of multiple ''weak learners'' is combined into a weighted sum that represents the final output of the boosted classifier. Usually, AdaBoost is presented for binary classification, although it can be generalized to multiple classes or bounded intervals of real values. AdaBoost is adaptive in the sense that subsequent weak learners (models) are adjusted in favor of instances misclassified by previous models. In some problems, it can be less susceptible to overfitting than other learning algorithms. The individual learners can be weak, but as long as the performance of each one is slightly better than random guessing, the final model can be proven to converge to a strong learner. Although AdaBo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
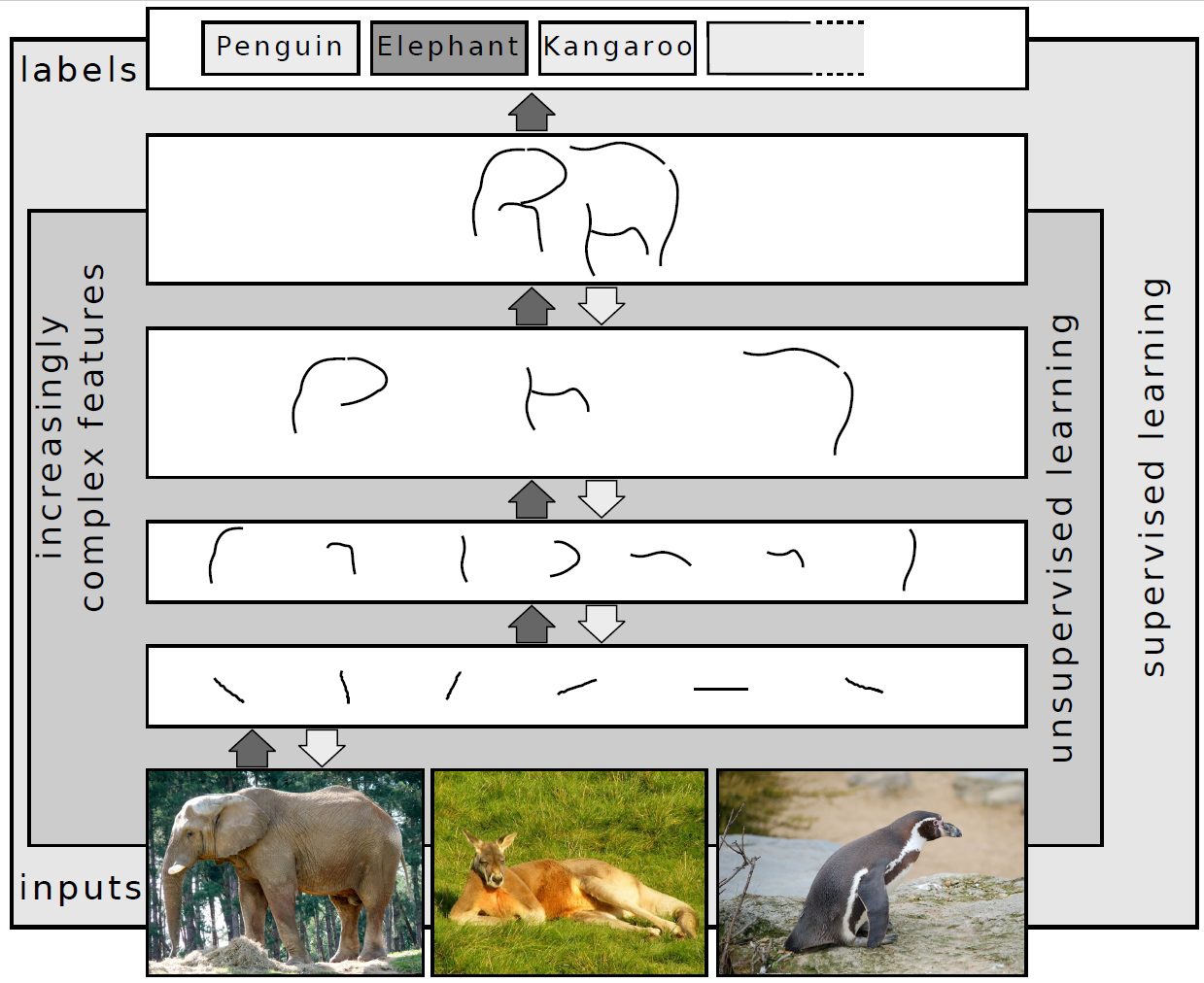
Deep Learning
Deep learning is a subset of machine learning that focuses on utilizing multilayered neural networks to perform tasks such as classification, regression, and representation learning. The field takes inspiration from biological neuroscience and is centered around stacking artificial neurons into layers and "training" them to process data. The adjective "deep" refers to the use of multiple layers (ranging from three to several hundred or thousands) in the network. Methods used can be either supervised, semi-supervised or unsupervised. Some common deep learning network architectures include fully connected networks, deep belief networks, recurrent neural networks, convolutional neural networks, generative adversarial networks, transformers, and neural radiance fields. These architectures have been applied to fields including computer vision, speech recognition, natural language processing, machine translation, bioinformatics, drug design, medical image analysis, c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
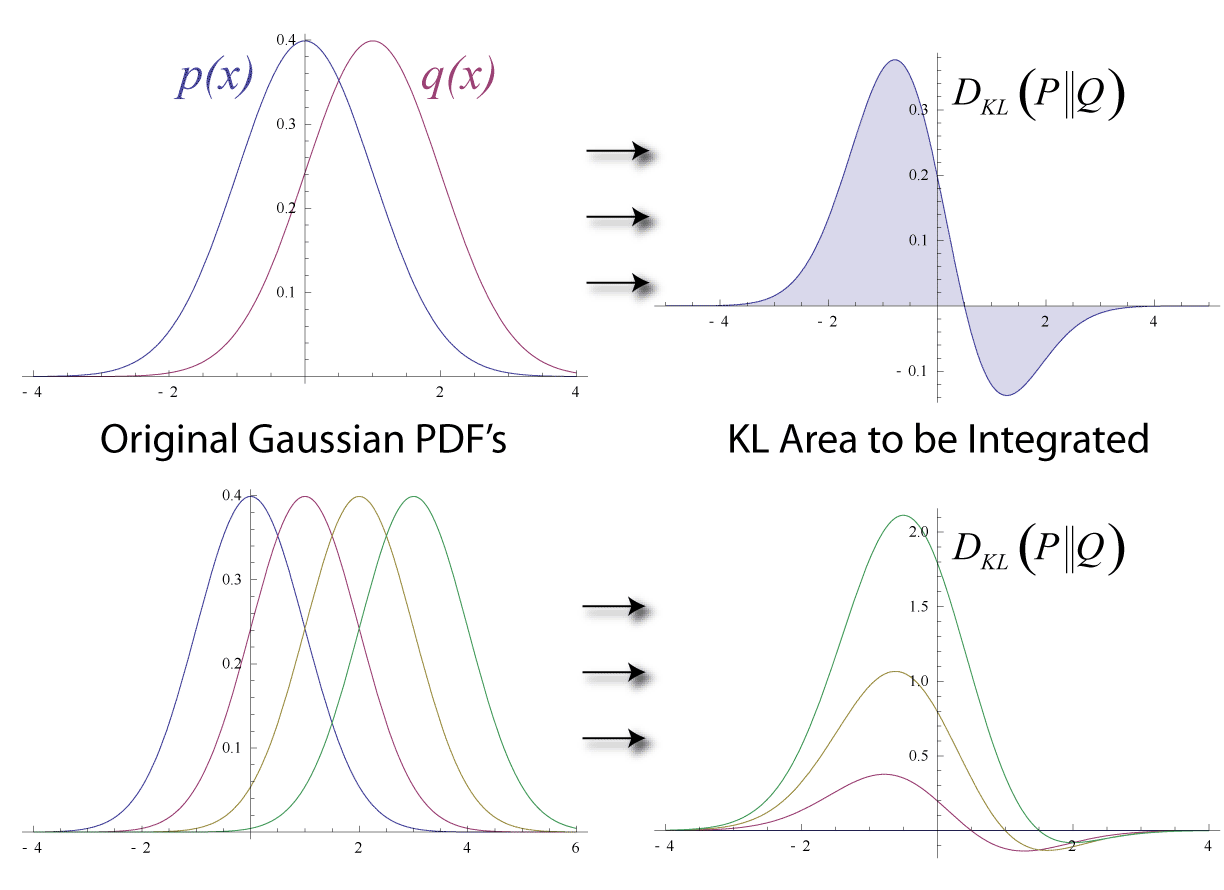
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for cer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |