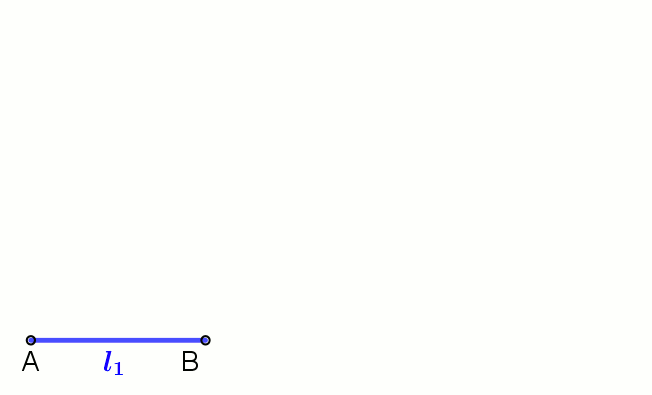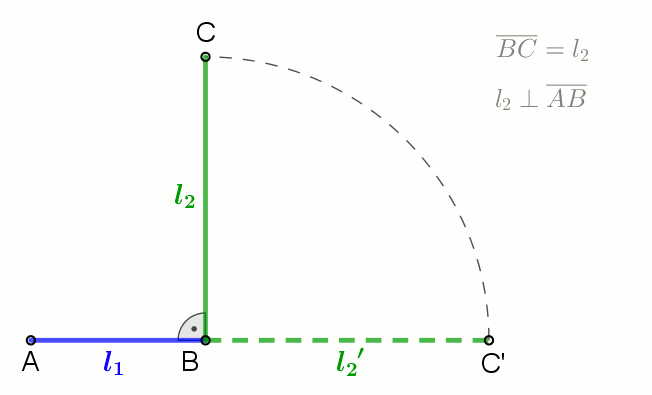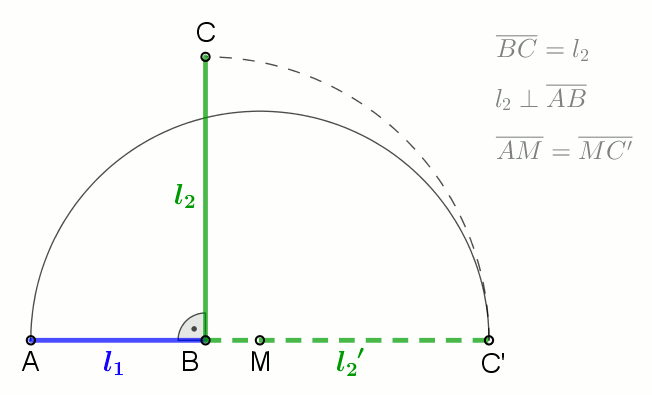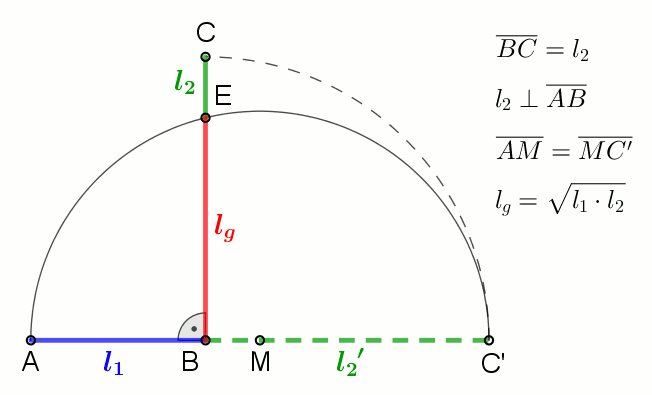|
Landen's Transformation
Landen's transformation is a mapping of the parameters of an elliptic integral, useful for the efficient numerical evaluation of elliptic functions. It was originally due to John Landen and independently rediscovered by Carl Friedrich Gauss. Statement The incomplete elliptic integral of the first kind is : F(\varphi \setminus \alpha) = F(\varphi, \sin \alpha) = \int_0^\varphi \frac, where \alpha is the modular angle. Landen's transformation states that if \alpha_0, \alpha_1, \varphi_0, \varphi_1 are such that (1 + \sin\alpha_1)(1 + \cos\alpha_0) = 2 and \tan(\varphi_1 - \varphi_0) = \cos\alpha_0 \tan \varphi_0, then :\begin F(\varphi_0 \setminus \alpha_0) &= (1 + \cos\alpha_0)^ F(\varphi_1 \setminus \alpha_1) \\ &= \tfrac(1 + \sin\alpha_1) F(\varphi_1 \setminus \alpha_1). \end Landen's transformation can similarly be expressed in terms of the elliptic modulus k = \sin\alpha and its complement k' = \cos\alpha. Complete elliptic integral In Gauss's formulation, the value of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Integral
In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals, which were first studied by Giulio Fagnano and Leonhard Euler (). Their name originates from their originally arising in connection with the problem of finding the arc length of an ellipse. Modern mathematics defines an "elliptic integral" as any function which can be expressed in the form f(x) = \int_^ R \left(t, \sqrt \right) \, dt, where is a rational function of its two arguments, is a polynomial of degree 3 or 4 with no repeated roots, and is a constant. In general, integrals in this form cannot be expressed in terms of elementary functions. Exceptions to this general rule are when has repeated roots, or when contains no odd powers of or if the integral is pseudo-elliptic. However, with the appropriate reduction formula, every elliptic integral can be brought into a form that involves integrals over rational functions and the three Leg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Landen
John Landen (23 January 1719 – 15 January 1790) was an English mathematician. Life He was born at Peakirk, near Peterborough in Northamptonshire, on 28 January 1719. He was brought up to the business of a surveyor, and acted as land agent to Earl Fitzwilliam, from 1762 to 1788. Cultivating mathematics during his leisure hours, he became a contributor to the ''Ladies' Diary'' in 1744, published ''Mathematical Lucubrations'' in 1755, and from 1754 onwards communicated to the Royal Society valuable investigations on points connected with the fluxionary calculus. His attempt to substitute for it a purely algebraic method, expounded in book i. of ''Residual Analysis'' was further prosecuted by Lagrange. Book ii. never appeared. Landen's transformation, for expressing a hyperbolic arc in terms of two elliptic arcs, was inserted in the ''Philosophical Transactions'' for 1775, and specimens of its use were given in the first volume of his ‘Mathematical Memoirs (1780). In a p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes referred to as the ''Princeps mathematicorum'' () and "the greatest mathematician since antiquity", Gauss had an exceptional influence in many fields of mathematics and science, and he is ranked among history's most influential mathematicians. Also available at Retrieved 23 February 2014. Comprehensive biographical article. Biography Early years Johann Carl Friedrich Gauss was born on 30 April 1777 in Brunswick (Braunschweig), in the Duchy of Brunswick-Wolfenbüttel (now part of Lower Saxony, Germany), to poor, working-class parents. His mother was illiterate and never recorded the date of his birth, remembering only that he had been born on a Wednesday, eight days before the Feast of the Ascension (which occurs 39 days after Easter). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Integral
In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals, which were first studied by Giulio Fagnano and Leonhard Euler (). Their name originates from their originally arising in connection with the problem of finding the arc length of an ellipse. Modern mathematics defines an "elliptic integral" as any function which can be expressed in the form f(x) = \int_^ R \left(t, \sqrt \right) \, dt, where is a rational function of its two arguments, is a polynomial of degree 3 or 4 with no repeated roots, and is a constant. In general, integrals in this form cannot be expressed in terms of elementary functions. Exceptions to this general rule are when has repeated roots, or when contains no odd powers of or if the integral is pseudo-elliptic. However, with the appropriate reduction formula, every elliptic integral can be brought into a form that involves integrals over rational functions and the three Leg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Eccentricity
Angular eccentricity is one of many parameters which arise in the study of the ellipse or ellipsoid. It is denoted here by α (alpha). It may be defined in terms of the eccentricity, ''e'', or the aspect ratio, ''b/a'' (the ratio of the semi-minor axis and the semi-major axis In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the lo ...): :\alpha=\sin^\!e=\cos^\left(\frac\right). \,\! Angular eccentricity is not currently used in English language publications on mathematics, geodesy or map projections but it does appear in older literature. Any non-dimensional parameter of the ellipse may be expressed in terms of the angular eccentricity. Such expressions are listed in the following table after the conventional definitions.Rapp, Richard H. (1991). ''Geometric Geodesy, Part I'', Dept. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Mean
In mathematics and statistics, the arithmetic mean ( ) or arithmetic average, or just the ''mean'' or the '' average'' (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results of an experiment or an observational study, or frequently a set of results from a survey. The term "arithmetic mean" is preferred in some contexts in mathematics and statistics, because it helps distinguish it from other means, such as the geometric mean and the harmonic mean. In addition to mathematics and statistics, the arithmetic mean is used frequently in many diverse fields such as economics, anthropology and history, and it is used in almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation's population. While the arithmetic mean is often used to report central tendencies, it is not a robust statistic, meaning that it is greatly in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the th root of the product of numbers, i.e., for a set of numbers , the geometric mean is defined as :\left(\prod_^n a_i\right)^\frac = \sqrt /math> or, equivalently, as the arithmetic mean in logscale: :\exp For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product, that is, \sqrt = 4. As another example, the geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2, that is, \sqrt = 1/2. The geometric mean applies only to positive numbers. The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as a set of growth figures: values of the human population or int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integration By Substitution
In calculus, integration by substitution, also known as ''u''-substitution, reverse chain rule or change of variables, is a method for evaluating integrals and antiderivatives. It is the counterpart to the chain rule for differentiation, and can loosely be thought of as using the chain rule "backwards". Substitution for a single variable Introduction Before stating the result rigorously, consider a simple case using indefinite integrals. Compute \textstyle\int(2x^3+1)^7(x^2)\,dx. Set u=2x^3+1. This means \textstyle\frac=6x^2, or in differential form, du=6x^2\,dx. Now :\int(2x^3 +1)^7(x^2)\,dx = \frac\int\underbrace_\underbrace_=\frac\int u^\,du=\frac\left(\fracu^\right)+C=\frac(2x^3+1)^+C, where C is an arbitrary constant of integration. This procedure is frequently used, but not all integrals are of a form that permits its use. In any event, the result should be verified by differentiating and comparing to the original integrand. :\frac\left frac(2x^3+1)^+C\r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Function
In mathematics, an algebraic function is a function that can be defined as the root of a polynomial equation. Quite often algebraic functions are algebraic expressions using a finite number of terms, involving only the algebraic operations addition, subtraction, multiplication, division, and raising to a fractional power. Examples of such functions are: * f(x) = 1/x * f(x) = \sqrt * f(x) = \frac Some algebraic functions, however, cannot be expressed by such finite expressions (this is the Abel–Ruffini theorem). This is the case, for example, for the Bring radical, which is the function implicitly defined by : f(x)^5+f(x)+x = 0. In more precise terms, an algebraic function of degree in one variable is a function y = f(x), that is continuous in its domain and satisfies a polynomial equation : a_n(x)y^n+a_(x)y^+\cdots+a_0(x)=0 where the coefficients are polynomial functions of , with integer coefficients. It can be shown that the same class of functions is obtained if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Legendre Form
In mathematics, the Legendre forms of elliptic integrals are a canonical set of three elliptic integrals to which all others may be reduced. Legendre chose the name ''elliptic integrals'' because the second kind gives the arc length of an ellipse of unit semi-major axis and eccentricity \scriptstyle (the ellipse being defined parametrically by \scriptstyle, \scriptstyle). In modern times the Legendre forms have largely been supplanted by an alternative canonical set, the Carlson symmetric forms. A more detailed treatment of the Legendre forms is given in the main article on elliptic integrals. Definition The incomplete elliptic integral of the first kind is defined as, :F(\phi,k) = \int_0^\phi \frac dt, the second kind as :E(\phi,k) = \int_0^\phi \sqrt\,dt, and the third kind as :\Pi(\phi,n,k) = \int_0^\phi \frac\,dt. The argument ''n'' of the third kind of integral is known as the characteristic, which in different notational conventions can appear as either the firs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |