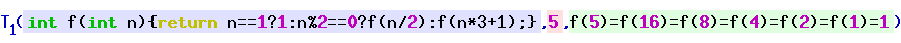|
Kleene's T Predicate
In computability theory, the T predicate, first studied by mathematician Stephen Cole Kleene, is a particular set of triples of natural numbers that is used to represent computable functions within formal theories of arithmetic. Informally, the ''T'' predicate tells whether a particular computer program will halt when run with a particular input, and the corresponding ''U'' function is used to obtain the results of the computation if the program does halt. As with the smn theorem, the original notation used by Kleene has become standard terminology for the concept.The predicate described here was presented in (Kleene 1943) and (Kleene 1952), and this is what is usually called "Kleene's ''T'' predicate". (Kleene 1967) uses the letter ''T'' to describe a different predicate related to computable functions, but which cannot be used to obtain Kleene's normal form theorem. Definition The definition depends on a suitable Gödel numbering that assigns natural numbers to computable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computability Theory
Computability theory, also known as recursion theory, is a branch of mathematical logic, computer science, and the theory of computation that originated in the 1930s with the study of computable functions and Turing degrees. The field has since expanded to include the study of generalized computability and definable set, definability. In these areas, computability theory overlaps with proof theory and effective descriptive set theory. Basic questions addressed by computability theory include: * What does it mean for a function (mathematics), function on the natural numbers to be computable? * How can noncomputable functions be classified into a hierarchy based on their level of noncomputability? Although there is considerable overlap in terms of knowledge and methods, mathematical computability theorists study the theory of relative computability, reducibility notions, and degree structures; those in the computer science field focus on the theory of computational complexity theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Primitive Recursive
In computability theory, a primitive recursive function is, roughly speaking, a function that can be computed by a computer program whose loops are all "for" loops (that is, an upper bound of the number of iterations of every loop is fixed before entering the loop). Primitive recursive functions form a strict subset of those general recursive functions that are also total functions. The importance of primitive recursive functions lies in the fact that most computable functions that are studied in number theory (and more generally in mathematics) are primitive recursive. For example, addition and division, the factorial and exponential function, and the function which returns the ''n''th prime are all primitive recursive. In fact, for showing that a computable function is primitive recursive, it suffices to show that its time complexity is bounded above by a primitive recursive function of the input size. It is hence not particularly easy to devise a computable function that is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Post's Theorem
In computability theory Post's theorem, named after Emil Post, describes the connection between the arithmetical hierarchy and the Turing degrees. Background The statement of Post's theorem uses several concepts relating to definability and recursion theory. This section gives a brief overview of these concepts, which are covered in depth in their respective articles. The arithmetical hierarchy classifies certain sets of natural numbers that are definable in the language of Peano arithmetic. A formula is said to be \Sigma^_m if it is an existential statement in prenex normal form (all quantifiers at the front) with m alternations between existential and universal quantifiers applied to a formula with bounded quantifiers only. Formally a formula \phi(s) in the language of Peano arithmetic is a \Sigma^_m formula if it is of the form :\left(\exists n^1_1\exists n^1_2\cdots\exists n^1_\right)\left(\forall n^2_1 \cdots \forall n^2_\right)\left(\exists n^3_1\cdots\right)\cdo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Halting Problem
In computability theory (computer science), computability theory, the halting problem is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running, or continue to run forever. The halting problem is ''Undecidable problem, undecidable'', meaning that no general algorithm exists that solves the halting problem for all possible program–input pairs. The problem comes up often in discussions of computability since it demonstrates that some functions are mathematically Definable set, definable but not Computable function, computable. A key part of the formal statement of the problem is a mathematical definition of a computer and program, usually via a Turing machine. The proof then shows, for any program that might determine whether programs halt, that a "pathological" program exists for which makes an incorrect determination. Specifically, is the program that, when called with some input, passes its own s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turing Degree
In computer science and mathematical logic the Turing degree (named after Alan Turing) or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set. Overview The concept of Turing degree is fundamental in computability theory, where sets of natural numbers are often regarded as decision problems. The Turing degree of a set is a measure of how difficult it is to solve the decision problem associated with the set, that is, to determine whether an arbitrary number is in the given set. Two sets are Turing equivalent if they have the same level of unsolvability; each Turing degree is a collection of Turing equivalent sets, so that two sets are in different Turing degrees exactly when they are not Turing equivalent. Furthermore, the Turing degrees are partially ordered, so that if the Turing degree of a set ''X'' is less than the Turing degree of a set ''Y'', then any (possibly noncomputable) procedure that correctly decides whether ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetical Hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene–Mostowski hierarchy (after mathematicians Stephen Cole Kleene and Andrzej Mostowski) classifies certain sets based on the complexity of formulas that define them. Any set that receives a classification is called arithmetical. The arithmetical hierarchy was invented independently by Kleene (1943) and Mostowski (1946).P. G. Hinman, ''Recursion-Theoretic Hierarchies'' (p.89), Perspectives in Logic, 1978. Springer-Verlag Berlin Heidelberg, ISBN 3-540-07904-1. The arithmetical hierarchy is important in computability theory, effective descriptive set theory, and the study of formal theories such as Peano arithmetic. The Tarski–Kuratowski algorithm provides an easy way to get an upper bound on the classifications assigned to a formula and the set it defines. The hyperarithmetical hierarchy and the analytical hierarchy extend the arithmetical hierarchy to classify additional formulas and set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turing Complete Set
In computability theory, a Turing reduction from a decision problem A to a decision problem B is an oracle machine that decides problem A given an oracle for B (Rogers 1967, Soare 1987) in finitely many steps. It can be understood as an algorithm that could be used to solve A if it had access to a subroutine for solving B. The concept can be analogously applied to function problems. If a Turing reduction from A to B exists, then every algorithm for B can be used to produce an algorithm for A, by inserting the algorithm for B at each place where the oracle machine computing A queries the oracle for B. However, because the oracle machine may query the oracle a large number of times, the resulting algorithm may require more time asymptotically than either the algorithm for B or the oracle machine computing A. A Turing reduction in which the oracle machine runs in polynomial time is known as a Cook reduction. The first formal definition of relative computability, then called relative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Recursive Function
In mathematical logic and computer science, a general recursive function, partial recursive function, or μ-recursive function is a partial function from natural numbers to natural numbers that is "computable" in an intuitive sense – as well as in a formal one. If the function is total, it is also called a total recursive function (sometimes shortened to recursive function). In computability theory, it is shown that the μ-recursive functions are precisely the functions that can be computed by Turing machines (this is one of the theorems that supports the Church–Turing thesis). The μ-recursive functions are closely related to primitive recursive functions, and their inductive definition (below) builds upon that of the primitive recursive functions. However, not every total recursive function is a primitive recursive function—the most famous example is the Ackermann function. Other equivalent classes of functions are the functions of lambda calculus and the functions tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Primitive Recursive Function
In computability theory, a primitive recursive function is, roughly speaking, a function that can be computed by a computer program whose loops are all "for" loops (that is, an upper bound of the number of iterations of every loop is fixed before entering the loop). Primitive recursive functions form a strict subset of those general recursive functions that are also total functions. The importance of primitive recursive functions lies in the fact that most computable functions that are studied in number theory (and more generally in mathematics) are primitive recursive. For example, addition and division, the factorial and exponential function, and the function which returns the ''n''th prime are all primitive recursive. In fact, for showing that a computable function is primitive recursive, it suffices to show that its time complexity is bounded above by a primitive recursive function of the input size. It is hence not particularly easy to devise a computable function th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peano Arithmetic
In mathematical logic, the Peano axioms (, ), also known as the Dedekind–Peano axioms or the Peano postulates, are axioms for the natural numbers presented by the 19th-century Italian mathematician Giuseppe Peano. These axioms have been used nearly unchanged in a number of metamathematical investigations, including research into fundamental questions of whether number theory is consistent and complete. The axiomatization of arithmetic provided by Peano axioms is commonly called Peano arithmetic. The importance of formalizing arithmetic was not well appreciated until the work of Hermann Grassmann, who showed in the 1860s that many facts in arithmetic could be derived from more basic facts about the successor operation and induction. In 1881, Charles Sanders Peirce provided an axiomatization of natural-number arithmetic. In 1888, Richard Dedekind proposed another axiomatization of natural-number arithmetic, and in 1889, Peano published a simplified version of them a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robinson Arithmetic
In mathematics, Robinson arithmetic is a finitely axiomatized fragment of first-order Peano arithmetic (PA), first set out by Raphael M. Robinson in 1950. It is usually denoted Q. Q is almost PA without the axiom schema of mathematical induction. Q is weaker than PA but it has the same language, and both theories are incomplete. Q is important and interesting because it is a finitely axiomatized fragment of PA that is recursively incompletable and essentially undecidable. Axioms The background logic of Q is first-order logic with identity, denoted by infix '='. The individuals, called natural numbers, are members of a set called N with a distinguished member 0, called zero. There are three operations over N: *A unary operation called successor and denoted by prefix ''S''; *Two binary operations, addition and multiplication, denoted by infix + and ·, respectively. The following axioms for Q are Q1–Q7 in (cf. also the axioms of first-order arithmetic). Variables ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |