|
Karnaugh–Veitch Map
A Karnaugh map (KM or K-map) is a diagram that can be used to simplify a Boolean algebra expression. Maurice Karnaugh introduced the technique in 1953 as a refinement of Edward W. Veitch's 1952 Veitch chart, which itself was a rediscovery of Allan Marquand's 1881 ''logical diagram'' or Marquand diagram. They are also known as Marquand–Veitch diagrams, Karnaugh–Veitch (KV) maps, and (rarely) Svoboda charts. An early advance in the history of formal logic methodology, Karnaugh maps remain relevant in the digital age, especially in the fields of logical circuit design and digital engineering. Definition A Karnaugh map reduces the need for extensive calculations by taking advantage of humans' pattern-recognition capability. It also permits the rapid identification and elimination of potential race conditions. The required Boolean results are transferred from a truth table onto a two-dimensional grid where, in Karnaugh maps, the cells are ordered in Gray code, and each ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karnaugh
Karnaugh is a surname. Notable people with the surname include: * Maurice Karnaugh (1924–2022), American physicist, mathematician, and inventor * Ron Karnaugh (born 1966), American retired swimmer See also * Karnaugh map {{surname ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional (programming)
In computer science, conditionals (that is, conditional statements, conditional expressions and conditional constructs) are programming language constructs that perform different computations or actions or return different values depending on the value of a Boolean expression, called a ''condition''. Conditionals are typically implemented by selectively executing instructions. Although dynamic dispatch is not usually classified as a conditional construct, it is another way to select between alternatives at runtime. Terminology Conditional statements are imperative constructs executed for side-effect, while conditional expressions return values. Many programming languages (such as C) have distinct conditional statements and conditional expressions. Although in pure functional programming, conditional expressions do not have side-effects, many languages with conditional expressions (such as Lisp) support conditional side-effects. If–then(–else) The if–then or if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solution
Solution may refer to: * Solution (chemistry), a mixture where one substance is dissolved in another * Solution (equation), in mathematics ** Numerical solution, in numerical analysis, approximate solutions within specified error bounds * Solution, in problem solving Problem solving is the process of achieving a goal by overcoming obstacles, a frequent part of most activities. Problems in need of solutions range from simple personal tasks (e.g. how to turn on an appliance) to complex issues in business an ... * A business solution is a method of organizing people and resources that can be sold as a product ** Solution, in solution selling Other uses * V-STOL Solution, an ultralight aircraft * Solution (band), a Dutch rock band ** ''Solution'' (Solution album), 1971 * Solution A.D., an American rock band * ''Solution'' (Cui Jian album), 1991 * ''Solutions'' (album), a 2019 album by K.Flay See also * Nature-based solutions * The Solution (other) * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Don't-care (logic)
In digital logic, a don't-care term (abbreviated DC, historically also known as ''redundancies'', ''irrelevancies'', ''optional entries'', ''invalid combinations'', ''vacuous combinations'', ''forbidden combinations'', ''unused states'' or ''logical remainders'') for a function is an input-sequence (a series of bits) for which the function output does not matter. An input that is known never to occur is a can't-happen term. Both these types of conditions are treated the same way in logic design and may be referred to collectively as ''don't-care conditions'' for brevity. The designer of a logic circuit to implement the function need not care about such inputs, but can choose the circuit's output arbitrarily, usually such that the simplest, smallest, fastest or cheapest circuit results ( minimization) or the power-consumption is minimized. Don't-care terms are important to consider in minimizing logic circuit design, including graphical methods like Karnaugh–Veitch maps and a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-map 6,8,9,10,11,12,13,14 Don't Care
A Karnaugh map (KM or K-map) is a diagram that can be used to simplify a Boolean algebra expression. Maurice Karnaugh introduced the technique in 1953 as a refinement of Edward W. Veitch's 1952 Veitch chart, which itself was a rediscovery of Allan Marquand's 1881 ''logical diagram'' or Marquand diagram. They are also known as Marquand–Veitch diagrams, Karnaugh–Veitch (KV) maps, and (rarely) Svoboda charts. An early advance in the history of formal logic methodology, Karnaugh maps remain relevant in the digital age, especially in the fields of logical circuit design and digital engineering. Definition A Karnaugh map reduces the need for extensive calculations by taking advantage of humans' pattern-recognition capability. It also permits the rapid identification and elimination of potential race conditions. The required Boolean results are transferred from a truth table onto a two-dimensional grid where, in Karnaugh maps, the cells are ordered in Gray code, and each c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product Of Sums
In Boolean algebra, any Boolean function can be expressed in the canonical disjunctive normal form ( CDNF), minterm canonical form, or Sum of Products (SoP or SOP) as a disjunction (OR) of minterms. The De Morgan dual is the canonical conjunctive normal form ( CCNF), maxterm canonical form, or Product of Sums (PoS or POS) which is a conjunction (AND) of maxterms. These forms can be useful for the simplification of Boolean functions, which is of great importance in the optimization of Boolean formulas in general and digital circuits in particular. Other canonical forms include the complete sum of prime implicants or Blake canonical form (and its dual), and the algebraic normal form (also called Zhegalkin or Reed–Muller). Minterms For a boolean function of n variables , a minterm is a product term in which each of the n variables appears ''exactly once'' (either in its complemented or uncomplemented form). Thus, a ''minterm'' is a logical expression of ''n'' variables that em ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
De Morgan's Laws
In propositional calculus, propositional logic and Boolean algebra, De Morgan's laws, also known as De Morgan's theorem, are a pair of transformation rules that are both Validity (logic), valid rule of inference, rules of inference. They are named after Augustus De Morgan, a 19th-century British mathematician. The rules allow the expression of Logical conjunction, conjunctions and Logical disjunction, disjunctions purely in terms of each other via logical negation, negation. The rules can be expressed in English as: * The negation of "A and B" is the same as "not A or not B". * The negation of "A or B" is the same as "not A and not B". or * The Complement (set theory), complement of the union of two sets is the same as the intersection of their complements * The complement of the intersection of two sets is the same as the union of their complements or * not (A or B) = (not A) and (not B) * not (A and B) = (not A) or (not B) where "A or B" is an "inclusive or" meaning ''at least' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-map 6,8,9,10,11,12,13,14
A Karnaugh map (KM or K-map) is a diagram that can be used to simplify a Boolean algebra expression. Maurice Karnaugh introduced the technique in 1953 as a refinement of Edward W. Veitch's 1952 Veitch chart, which itself was a rediscovery of Allan Marquand's 1881 ''logical diagram'' or Marquand diagram. They are also known as Marquand–Veitch diagrams, Karnaugh–Veitch (KV) maps, and (rarely) Svoboda charts. An early advance in the history of formal logic methodology, Karnaugh maps remain relevant in the digital age, especially in the fields of logical circuit design and digital engineering. Definition A Karnaugh map reduces the need for extensive calculations by taking advantage of humans' pattern-recognition capability. It also permits the rapid identification and elimination of potential race conditions. The required Boolean results are transferred from a truth table onto a two-dimensional grid where, in Karnaugh maps, the cells are ordered in Gray code, and each c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
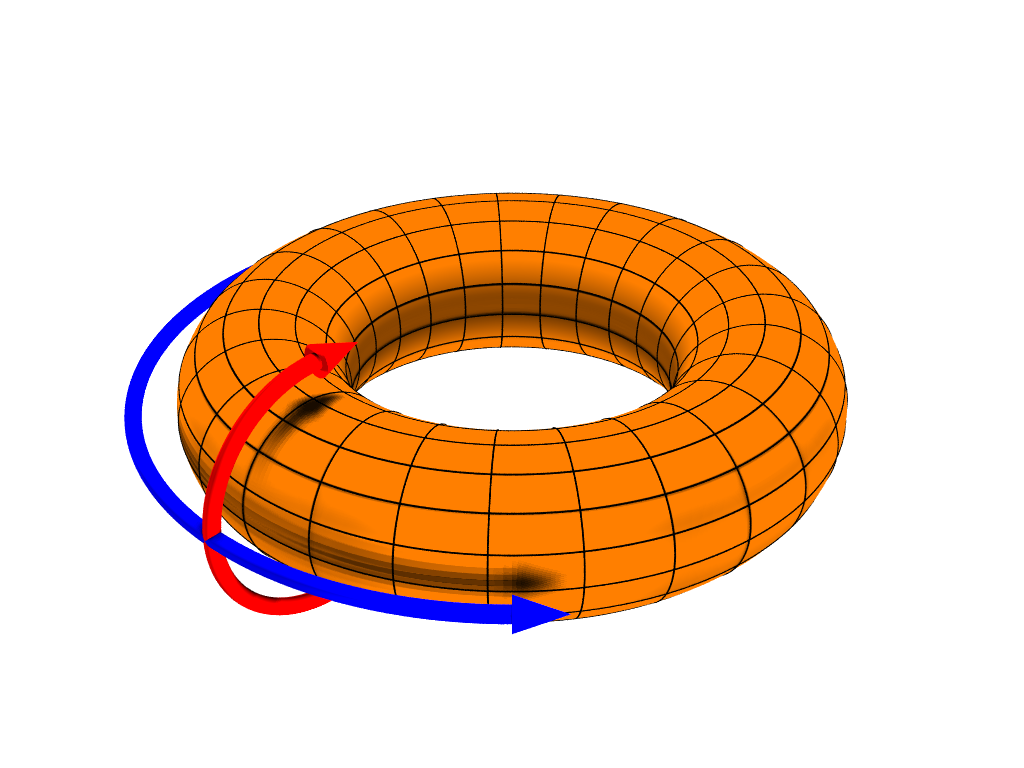
Torus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a Lemon (geometry), spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus From Rectangle
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution, also known as a ring torus. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. Real-world objects that appro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-map Minterms A
A Karnaugh map (KM or K-map) is a diagram that can be used to simplify a Boolean algebra expression. Maurice Karnaugh introduced the technique in 1953 as a refinement of Edward W. Veitch's 1952 Veitch chart, which itself was a rediscovery of Allan Marquand's 1881 ''logical diagram'' or Marquand diagram. They are also known as Marquand–Veitch diagrams, Karnaugh–Veitch (KV) maps, and (rarely) Svoboda charts. An early advance in the history of formal logic methodology, Karnaugh maps remain relevant in the digital age, especially in the fields of logical circuit design and digital engineering. Definition A Karnaugh map reduces the need for extensive calculations by taking advantage of humans' pattern-recognition capability. It also permits the rapid identification and elimination of potential race conditions. The required Boolean results are transferred from a truth table onto a two-dimensional grid where, in Karnaugh maps, the cells are ordered in Gray code, and each c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karnaugh Map Torus
{{surname ...
Karnaugh is a surname. Notable people with the surname include: * Maurice Karnaugh (1924–2022), American physicist, mathematician, and inventor * Ron Karnaugh (born 1966), American retired swimmer See also * Karnaugh map A Karnaugh map (KM or K-map) is a diagram that can be used to simplify a Boolean algebra expression. Maurice Karnaugh introduced the technique in 1953 as a refinement of Edward W. Veitch's 1952 Veitch chart, which itself was a rediscovery of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |