|
Horopter
In vision science, the horopter was originally defined in geometric terms as the Locus (geometry), locus of points in space that make the same angle at each eye with the Fixation (visual), fixation point, although more recently in studies of binocular vision it is taken to be the locus of points in space that have the same binocular disparity, disparity as fixation. This can be defined theoretically as the points in space that project on corresponding points in the two retinas, that is, on anatomically identical points. The horopter can be measured empirically in which it is defined using some criterion. The concept of horopter can then be extended as a geometrical locus of points in space where a specific condition is met: * the binocular horopter is the locus of iso-disparity points in space; * the oculomotor horopter is the locus of iso-vergence points in space. As other quantities that describe the functional principles of the visual system, it is possible to provide a theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binocular Vision
Binocular vision is seeing with two eyes. The Field_of_view, field of view that can be surveyed with two eyes is greater than with one eye. To the extent that the visual fields of the two eyes overlap, #Depth, binocular depth can be perceived. This allows objects to be recognized more quickly, camouflage to be detected, spatial relationships to be perceived more quickly and accurately (#Stereopsis, stereopsis) and perception to be less susceptible to optical illusions, optical illusions. In secion #Medical, Medical attention is paid to the occurrence, defects and sharpness of binocular vision. In section #Biological, Biological the occurrence of binocular vision in animals is described. Geometric terms When the left eye (LE) and the right eye (RE) observe two objects X and Y, the following concepts are important:Krol J.D.(1982),"Perceptual ghosts in stereopsis, a ghosly problem in binocular vision", PhD thesis ISBN 90-9000382-7.Koenderink J.J.;van Doorn A.J. (1976) "Geometry of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Horopter
In vision science, the horopter was originally defined in geometric terms as the Locus (geometry), locus of points in space that make the same angle at each eye with the Fixation (visual), fixation point, although more recently in studies of binocular vision it is taken to be the locus of points in space that have the same binocular disparity, disparity as fixation. This can be defined theoretically as the points in space that project on corresponding points in the two retinas, that is, on anatomically identical points. The horopter can be measured empirically in which it is defined using some criterion. The concept of horopter can then be extended as a geometrical locus of points in space where a specific condition is met: * the binocular horopter is the locus of iso-disparity points in space; * the oculomotor horopter is the locus of iso-vergence points in space. As other quantities that describe the functional principles of the visual system, it is possible to provide a theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ibn Al-Haytham
Ḥasan Ibn al-Haytham (Latinization of names, Latinized as Alhazen; ; full name ; ) was a medieval Mathematics in medieval Islam, mathematician, Astronomy in the medieval Islamic world, astronomer, and Physics in the medieval Islamic world, physicist of the Islamic Golden Age from present-day Iraq.For the description of his main fields, see e.g. ("He is one of the principal Arab mathematicians and, without any doubt, the best physicist.") , ("Ibn al-Ḥaytam was an eminent eleventh-century Arab optician, geometer, arithmetician, algebraist, astronomer, and engineer."), ("Ibn al-Haytham (d. 1039), known in the West as Alhazan, was a leading Arab mathematician, astronomer, and physicist. His optical compendium, Kitab al-Manazir, is the greatest medieval work on optics.") Referred to as "the father of modern optics", he made significant contributions to the principles of optics and visual perception in particular. His most influential work is titled ''Book of Optics, Kit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peter Ludvig Panum
Peter Ludvig Panum (19 December 1820 – 2 May 1885) was a Danish physiologist and pathologist born on the island of Bornholm in Rønne. He founded studies in exercise physiology at the University of Copenhagen. The Panum Institute in Copenhagen is named in his honor. Early life and education Panum was born in Rønne on the island of Bornholm, the son of regiment surgeon Jens Severin Nathanael Panum (1792-1836) and Johanne Caroline Louise Charlotte Lande (1798-1844). The family moved to Eckernförde (Rendsburg) in 1829, where his father had assumed a position as regiment surgeon. After matriculating from Flensburg Learned School in 1840, Panum enrolled first at Kiel University before in 1841 transferring to the University of Copenhagen. Career After completing his medical studies in 1845, Panum assumed a position at Almindelig Hospital in Copenhagen. During 1846 he was chosen by the government to undertake research of a measles epidemic in the Faroe Islands. As a result o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charles Wheatstone
Sir Charles Wheatstone (; 6 February 1802 – 19 October 1875) was an English physicist and inventor best known for his contributions to the development of the Wheatstone bridge, originally invented by Samuel Hunter Christie, which is used to measure an unknown electrical resistance, and as a major figure in the development of telegraphy. His other contributions include the English concertina, the stereoscope (a device for displaying three-dimensional images) and the Playfair cipher (an encryption technique). Life Charles Wheatstone was born in Barnwood, Gloucestershire. His father, W. Wheatstone, was a music-seller in the town, who moved to 128 Pall Mall, London, four years later, becoming a teacher of the flute. Charles, the second son, went to a village school, near Gloucester, and afterwards to several institutions in London. One of them was in Kennington, and kept by a Mrs. Castlemaine, who was astonished at his rapid progress. From another he ran away, but was captured ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problem (mathematics education), word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; and they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection (mathematics)
In mathematics, a projection is an idempotent mapping of a set (or other mathematical structure) into a subset (or sub-structure). In this case, idempotent means that projecting twice is the same as projecting once. The restriction to a subspace of a projection is also called a ''projection'', even if the idempotence property is lost. An everyday example of a projection is the casting of shadows onto a plane (sheet of paper): the projection of a point is its shadow on the sheet of paper, and the projection (shadow) of a point on the sheet of paper is that point itself (idempotency). The shadow of a three-dimensional sphere is a disk. Originally, the notion of projection was introduced in Euclidean geometry to denote the projection of the three-dimensional Euclidean space onto a plane in it, like the shadow example. The two main projections of this kind are: * The projection from a point onto a plane or central projection: If is a point, called the center of projection, then t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
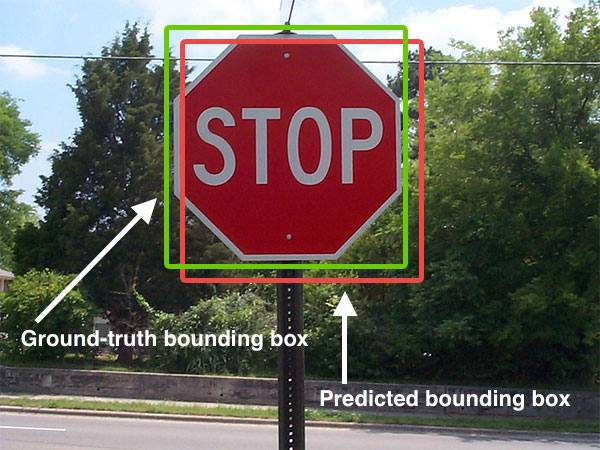
Computer Vision
Computer vision tasks include methods for image sensor, acquiring, Image processing, processing, Image analysis, analyzing, and understanding digital images, and extraction of high-dimensional data from the real world in order to produce numerical or symbolic information, e.g. in the form of decisions. "Understanding" in this context signifies the transformation of visual images (the input to the retina) into descriptions of the world that make sense to thought processes and can elicit appropriate action. This image understanding can be seen as the disentangling of symbolic information from image data using models constructed with the aid of geometry, physics, statistics, and learning theory. The scientific discipline of computer vision is concerned with the theory behind artificial systems that extract information from images. Image data can take many forms, such as video sequences, views from multiple cameras, multi-dimensional data from a 3D scanning, 3D scanner, 3D point clouds ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diplopia
Diplopia is the simultaneous perception of two images of a single object that may be displaced in relation to each other. Also called double vision, it is a loss of visual focus under regular conditions, and is often voluntary. However, when occurring involuntarily, it results from impaired function of the extraocular muscles, where both eyes are still functional, but they cannot turn to target the desired object. Problems with these muscles may be due to mechanical problems, disorders of the neuromuscular junction, disorders of the cranial nerves ( III, IV, and VI) that innervate the muscles, and occasionally disorders involving the supranuclear oculomotor pathways or ingestion of toxins. Diplopia can be one of the first signs of a systemic disease, particularly to a muscular or neurological process, and it may disrupt a person's balance, movement, or reading abilities. Causes Diplopia has a diverse range of ophthalmologic, infectious, autoimmune, neurological, and neoplasti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Twisted Cubic
In mathematics, a twisted cubic is a smooth, rational curve ''C'' of degree three in projective 3-space P3. It is a fundamental example of a skew curve. It is essentially unique, up to projective transformation (''the'' twisted cubic, therefore). In algebraic geometry, the twisted cubic is a simple example of a projective variety that is not linear or a hypersurface, in fact not a complete intersection. It is the three-dimensional case of the rational normal curve, and is the image of a Veronese map of degree three on the projective line. Definition The twisted cubic is most easily given parametrically as the image of the map :\nu:\mathbf^1\to\mathbf^3 which assigns to the homogeneous coordinate :T/math> the value :\nu: :T\mapsto ^3:S^2T:ST^2:T^3 In one coordinate patch of projective space, the map is simply the moment curve :\nu:x \mapsto (x,x^2,x^3) That is, it is the closure by a single point at infinity of the affine curve (x,x^2,x^3). The twisted cubic is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ewald Hering
Karl Ewald Konstantin Hering (5 August 1834 – 26 January 1918) was a German physiologist who did much research in color vision, binocular perception, eye movements, and hyperacuity. He proposed opponent color theory in 1892. Born in Gersdorf, Saxony, Alt-Gersdorf, Kingdom of Saxony, Hering studied at the University of Leipzig and became the first rector of the Karl-Ferdinands-Universität, German Charles-Ferdinand University in Prague. Biography Early years Hering was born in Alt-Gersdorf in Saxony, Germany. He probably grew up in a poor family, son of a Lutheran pastor. Hering attended gymnasium in Zittau and entered the university of Leipzig in 1853. There he studied philosophy, zoology and medicine. He completed an M.D. degree in 1860. It is somewhat unclear how Hering trained to do research. At the time Johannes Peter Müller was perhaps the most famous physiologist in Germany. Hering seems to have applied for studying under his direction but was rejected, which m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |