|
Hilbert Transform
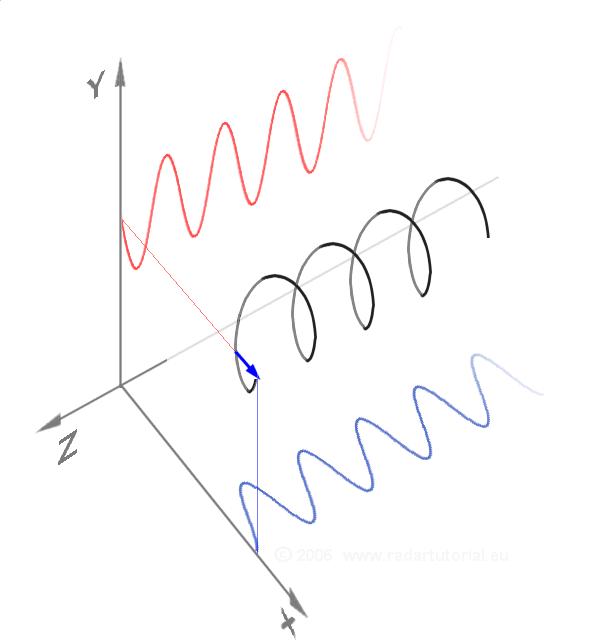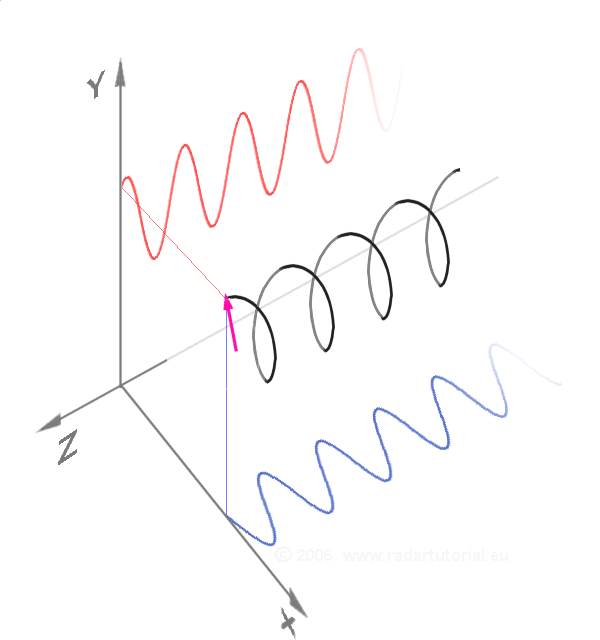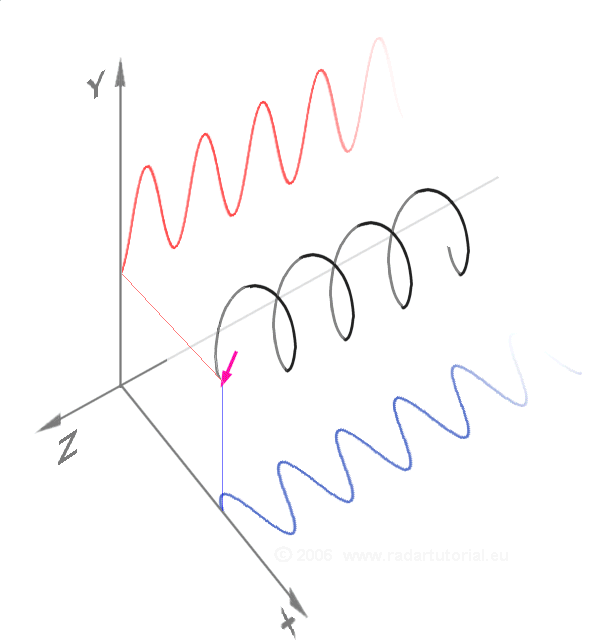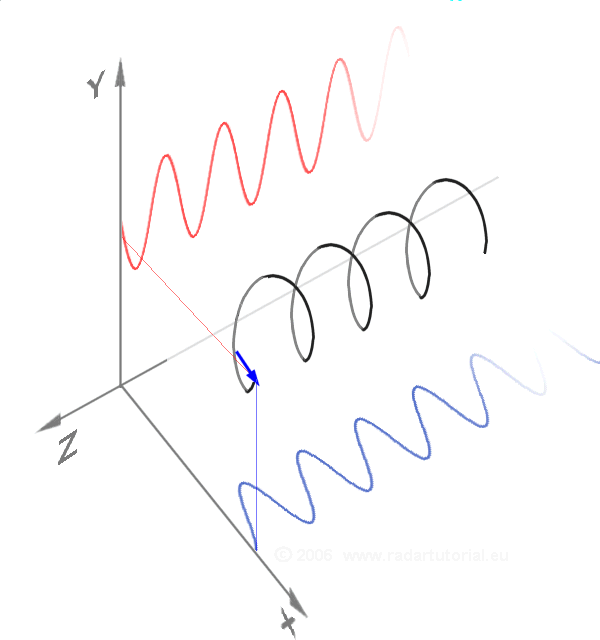
In mathematics and signal processing, the Hilbert transform is a specific singular integral that takes a function, of a real variable and produces another function of a real variable . The Hilbert transform is given by the Cauchy principal value of the convolution with the function 1/(\pi t) (see ). The Hilbert transform has a particularly simple representation in the frequency domain: It imparts a phase shift of ±90° (/2 radians) to every frequency component of a function, the sign of the shift depending on the sign of the frequency (see ). The Hilbert transform is important in signal processing, where it is a component of the Analytic signal, analytic representation of a real-valued signal . The Hilbert transform was first introduced by David Hilbert in this setting, to solve a special case of the Riemann–Hilbert problem for analytic functions. Definition The Hilbert transform of can be thought of as the convolution of with the function , known as the Cauchy ker ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lp Space
In mathematics, the spaces are function spaces defined using a natural generalization of the -norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue , although according to the Bourbaki group they were first introduced by Frigyes Riesz . spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces. Because of their key role in the mathematical analysis of measure and probability spaces, Lebesgue spaces are used also in the theoretical discussion of problems in physics, statistics, economics, finance, engineering, and other disciplines. Preliminaries The -norm in finite dimensions The Euclidean length of a vector x = (x_1, x_2, \dots, x_n) in the n-dimensional real vector space \Reals^n is given by the Euclidean norm: \, x\, _2 = \left(^2 + ^2 + \dotsb + ^2\right)^. The Euclidean distance between two points x and y is the length \, x - y\, _2 of the straight line b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indicator Function
In mathematics, an indicator function or a characteristic function of a subset of a set is a function that maps elements of the subset to one, and all other elements to zero. That is, if is a subset of some set , then the indicator function of is the function \mathbf_A defined by \mathbf_\!(x) = 1 if x \in A, and \mathbf_\!(x) = 0 otherwise. Other common notations are and \chi_A. The indicator function of is the Iverson bracket of the property of belonging to ; that is, \mathbf_(x) = \left x\in A\ \right For example, the Dirichlet function is the indicator function of the rational numbers as a subset of the real numbers. Definition Given an arbitrary set , the indicator function of a subset of is the function \mathbf_A \colon X \mapsto \ defined by \operatorname\mathbf_A\!( x ) = \begin 1 & \text x \in A \\ 0 & \text x \notin A \,. \end The Iverson bracket provides the equivalent notation \left x\in A\ \right/math> or that can be used instead of \mathbf_\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Delta Function
In mathematical analysis, the Dirac delta function (or distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Thus it can be Heuristic, represented heuristically as \delta (x) = \begin 0, & x \neq 0 \\ , & x = 0 \end such that \int_^ \delta(x) dx=1. Since there is no function having this property, modelling the delta "function" rigorously involves the use of limit (mathematics), limits or, as is common in mathematics, measure theory and the theory of distribution (mathematics), distributions. The delta function was introduced by physicist Paul Dirac, and has since been applied routinely in physics and engineering to model point masses and instantaneous impulses. It is called the delta function because it is a continuous analogue of the Kronecker delta function, which is usually defined on a discrete domain and takes values ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinc Function
In mathematics, physics and engineering, the sinc function ( ), denoted by , has two forms, normalized and unnormalized.. In mathematics, the historical unnormalized sinc function is defined for by \operatorname(x) = \frac. Alternatively, the unnormalized sinc function is often called the sampling function, indicated as Sa(''x''). In digital signal processing and information theory, the normalized sinc function is commonly defined for by \operatorname(x) = \frac. In either case, the value at is defined to be the limiting value \operatorname(0) := \lim_\frac = 1 for all real (the limit can be proven using the squeeze theorem). The normalization causes the definite integral of the function over the real numbers to equal 1 (whereas the same integral of the unnormalized sinc function has a value of ). As a further useful property, the zeros of the normalized sinc function are the nonzero integer values of . The normalized sinc function is the Fourier transform of the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dawson Function
In mathematics, the Dawson function or Dawson integral (named after H. G. Dawson) is the one-sided Fourier–Laplace sine transform of the Gaussian function. Definition The Dawson function is defined as either: D_+(x) = e^ \int_0^x e^\,dt, also denoted as F(x) or D(x), or alternatively D_-(x) = e^ \int_0^x e^\,dt.\! The Dawson function is the one-sided Fourier–Laplace sine transform of the Gaussian function, D_+(x) = \frac12 \int_0^\infty e^\,\sin(xt)\,dt. It is closely related to the error function erf, as : D_+(x) = e^ \operatorname (x) = - e^ \operatorname (ix) where erfi is the imaginary error function, Similarly, D_-(x) = \frac e^ \operatorname(x) in terms of the real error function, erf. In terms of either erfi or the Faddeeva function w(z), the Dawson function can be extended to the entire complex plane:Mofreh R. Zaghloul and Ahmed N. Ali,Algorithm 916: Computing the Faddeyeva and Voigt Functions" ''ACM Trans. Math. Soft.'' 38 (2), 15 (2011). Preprint availa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio signals (sound), radio waves, and light. The interval of time between events is called the period. It is the reciprocal of the frequency. For example, if a heart beats at a frequency of 120 times per minute (2 hertz), its period is one half of a second. Special definitions of frequency are used in certain contexts, such as the angular frequency in rotational or cyclical properties, when the rate of angular progress is measured. Spatial frequency is defined for properties that vary or cccur repeatedly in geometry or space. The unit of measurement of frequency in the International System of Units (SI) is the hertz, having the symbol Hz. Definitions and units For cyclical phenomena such as oscillations, waves, or for examp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Negative Frequency
In mathematics, the concept of signed frequency (negative and positive frequency) can indicate both the rate and sense of rotation; it can be as simple as a wheel rotating clockwise or counterclockwise. The rate is expressed in units such as revolutions (a.k.a. ''cycles'') per second (hertz) or radian/second (where 1 cycle corresponds to 2''π'' radians). Example: Mathematically, the vector (\cos(t), \sin(t)) has a positive frequency of +1 radian per unit of time and rotates counterclockwise around a unit circle, while the vector (\cos(-t), \sin(-t)) has a negative frequency of −1 radian per unit of time, which rotates clockwise instead. Sinusoids Let be an angular frequency with units of radians/second. Then the function has slope , which is called a negative frequency. But when the function is used as the argument of a cosine operator, the result is indistinguishable from . Similarly, is indistinguishable from . Thus any sinusoid can be represented in terms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number , one has e^ = \cos x + i \sin x, where is the base of the natural logarithm, is the imaginary unit, and and are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted ("cosine plus ''i'' sine"). The formula is still valid if is a complex number, and is also called ''Euler's formula'' in this more general case. Euler's formula is ubiquitous in mathematics, physics, chemistry, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics". When , Euler's formula may be rewritten as or , which is known as Euler's identity. History In 1714, the English mathematician Roger Cotes prese ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sign Function
In mathematics, the sign function or signum function (from '' signum'', Latin for "sign") is a function that has the value , or according to whether the sign of a given real number is positive or negative, or the given number is itself zero. In mathematical notation the sign function is often represented as \sgn x or \sgn (x). Definition The signum function of a real number x is a piecewise function which is defined as follows: \sgn x :=\begin -1 & \text x 0. \end The law of trichotomy states that every real number must be positive, negative or zero. The signum function denotes which unique category a number falls into by mapping it to one of the values , or which can then be used in mathematical expressions or further calculations. For example: \begin \sgn(2) &=& +1\,, \\ \sgn(\pi) &=& +1\,, \\ \sgn(-8) &=& -1\,, \\ \sgn(-\frac) &=& -1\,, \\ \sgn(0) &=& 0\,. \end Basic properties Any real number can be expressed as the product of its absolute value and its sig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplier (Fourier Analysis)
In Fourier analysis, a multiplier operator is a type of linear operator, or transformation of functions. These operators act on a function by altering its Fourier transform. Specifically they multiply the Fourier transform of a function by a specified function known as the multiplier or symbol. Occasionally, the term ''multiplier operator'' itself is shortened simply to ''multiplier''. In simple terms, the multiplier reshapes the frequencies involved in any function. This class of operators turns out to be broad: general theory shows that a translation-invariant operator on a group which obeys some (very mild) regularity conditions can be expressed as a multiplier operator, and conversely. Many familiar operators, such as translations and differentiation, are multiplier operators, although there are many more complicated examples such as the Hilbert transform. In signal processing, a multiplier operator is called a " filter", and the multiplier is the filter's frequency response ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alberto Calderón
Alberto Pedro Calderón (September 14, 1920 – April 16, 1998) was an Argentine mathematician. His name is associated with the University of Buenos Aires, but first and foremost with the University of Chicago, where Calderón and his mentor, the analyst Antoni Zygmund, developed the theory of singular integral operators. This created the " Chicago School of (hard) Analysis" (sometimes simply known as the "Calderón-Zygmund School"). Calderón's work ranged over a wide variety of topics: from singular integral operators to partial differential equations, from interpolation theory to Cauchy integrals on Lipschitz curves, from ergodic theory to inverse problems in electrical prospection. Calderón's work has also had a powerful impact on practical applications including signal processing, geophysics, and tomography. Early life and education Alberto Pedro Calderón was born on September 14, 1920, in Mendoza, Argentina, to Don Pedro Calderón, a physician (urologist), and Haydée ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |