|
Hexagonal Lattice
The hexagonal lattice (sometimes called triangular lattice) is one of the five two-dimensional Bravais lattice types. The symmetry category of the lattice is wallpaper group p6m. The primitive translation vectors of the hexagonal lattice form an angle of 120° and are of equal lengths, : , \mathbf a_1, = , \mathbf a_2, = a. The reciprocal lattice of the hexagonal lattice is a hexagonal lattice in reciprocal space with orientation changed by 90° and primitive lattice vectors of length : g=\frac. Honeycomb point set The honeycomb point set is a special case of the hexagonal lattice with a two-atom basis. The centers of the hexagons of a honeycomb form a hexagonal lattice, and the honeycomb point set can be seen as the union of two offset hexagonal lattices. In nature, carbon atoms of the two-dimensional material graphene are arranged in a honeycomb point set. Crystal classes The ''hexagonal lattice'' class names, Schönflies notation, Hermann-Mauguin notation, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equilateral Triangle Lattice
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the special case of an isosceles triangle by modern definition, creating more special properties. The equilateral triangle can be found in various Tessellation, tilings, and in polyhedrons such as the deltahedron and antiprism. It appears in real life in popular culture, architecture, and the study of stereochemistry resembling the molecular known as the trigonal planar molecular geometry. Properties An equilateral triangle is a triangle that has three equal sides. It is a special case of an isosceles triangle in the modern definition, stating that an isosceles triangle is defined at least as having two equal sides. Based on the modern definition, this leads to an equilateral triangle in which one of the three sides may be considered its b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermite Constant
In mathematics, the Hermite constant, named after Charles Hermite, determines how long a shortest element of a lattice in Euclidean space can be. The constant ''γn'' for integers ''n'' > 0 is defined as follows. For a lattice ''L'' in Euclidean space R''n'' with unit covolume, i.e. vol(R''n''/''L'') = 1, let ''λ''1(''L'') denote the least length of a nonzero element of ''L''. Then is the maximum of ''λ''1(''L'') over all such lattices ''L''. The square root in the definition of the Hermite constant is a matter of historical convention. Alternatively, the Hermite constant ''γn'' can be defined as the square of the maximal systole of a flat ''n''-dimensional torus of unit volume. Example The Hermite constant is known in dimensions 1–8 and 24. For ''n'' = 2, one has ''γ''2 = . This value is attained by the hexagonal lattice of the Eisenstein integers, scaled to have a fundamental parallelogram with unit area. The constants for the missing values are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Voronoi Diagram
In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. It can be classified also as a tessellation. In the simplest case, these objects are just finitely many points in the plane (called seeds, sites, or generators). For each seed there is a corresponding region, called a Voronoi cell, consisting of all points of the plane closer to that seed than to any other. The Voronoi diagram of a set of points is dual to that set's Delaunay triangulation. The Voronoi diagram is named after mathematician Georgy Voronoy, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet). Voronoi cells are also known as Thiessen polygons, after Alfred H. Thiessen. Voronoi diagrams have practical and theoretical applications in many fields, mainly in science and technology, but also in visual art. Simplest case In the simplest case, shown in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
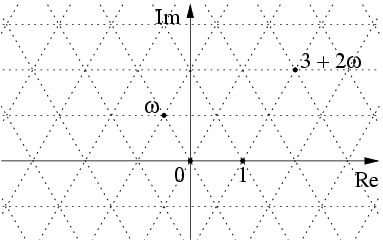
Eisenstein Integer
In mathematics, the Eisenstein integers (named after Gotthold Eisenstein), occasionally also known as Eulerian integers (after Leonhard Euler), are the complex numbers of the form : z = a + b\omega , where and are integers and : \omega = \frac = e^ is a Root of unity#General definition, primitive (hence non-real) cube root of unity. The Eisenstein integers form a triangular lattice in the complex plane, in contrast with the Gaussian integers, which form a square lattice in the complex plane. The Eisenstein integers are a Countable set, countably infinite set. Properties The Eisenstein integers form a commutative ring of algebraic integers in the algebraic number field – the third cyclotomic field. To see that the Eisenstein integers are algebraic integers note that each is a root of the monic polynomial : z^2 - (2a - b)\;\!z + \left(a^2 - ab + b^2\right)~. In particular, satisfies the equation : \omega^2 + \omega + 1 = 0~. The product of two Eisenstein integers and i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Centered Hexagonal Number
In mathematics and combinatorics, a centered hexagonal number, or centered hexagon number, is a centered polygonal number, centered figurate number that represents a hexagon with a dot in the center and all other dots surrounding the center dot in a hexagonal lattice. The following figures illustrate this arrangement for the first four centered hexagonal numbers: : Centered hexagonal numbers should not be confused with hexagonal number, cornered hexagonal numbers, which are figurate numbers in which the associated hexagons share a vertex. The sequence of hexagonal numbers starts out as follows : :1, 7, 19 (number), 19, 37 (number), 37, 61 (number), 61, 91 (number), 91, 127 (number), 127, 169 (number), 169, 217 (number), 217, 271 (number), 271, 331 (number), 331, 397 (number), 397, 469, 547, 631, 721, 817, 919. Formula The th centered hexagonal number is given by the formula :H(n) = n^3 - (n-1)^3 = 3n(n-1)+1 = 3n^2 - 3n +1. \, Expressing the formula as :H(n) = 1+6\left(\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Close-packing
In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement (or lattice). Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a lattice packing is :\frac \approx 0.74048. The same packing density can also be achieved by alternate stackings of the same close-packed planes of spheres, including structures that are aperiodic in the stacking direction. The Kepler conjecture states that this is the highest density that can be achieved by any arrangement of spheres, either regular or irregular. This conjecture was proven by Thomas Hales. The highest density is so far known only for 1, 2, 3, 8, and 24 dimensions. Many crystal structures are based on a close-packing of a single kind of atom, or a close-packing of large ions with smaller ions filling the spaces between them. The cubic and hexagonal arrangements are very cl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal Tiling
In geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which exactly three hexagons meet at each vertex. It has Schläfli symbol of or (as a Truncation (geometry), truncated triangular tiling). English mathematician John Horton Conway, John Conway called it a hextille. The internal angle of the hexagon is 120 degrees, so three hexagons at a point make a full 360 degrees. It is one of List of regular polytopes#Euclidean tilings, three regular tilings of the plane. The other two are the triangular tiling and the square tiling. Structure and properties The hexagonal tiling has a structure consisting of a regular hexagon only as its prototile, sharing two vertices with other identical ones, an example of monohedral tiling. Each vertex at the tiling is surrounded by three regular hexagons, denoted as 6.6.6 by vertex configuration. The dual of a hexagonal tiling is triangular tiling, because the center of each hexagonal tiling ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Lattice
In mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice, denoted as . It is one of the five types of two-dimensional lattices as classified by their symmetry groups; its symmetry group in IUC notation as , Coxeter notation as , and orbifold notation as . Two orientations of an image of the lattice are by far the most common. They can conveniently be referred to as the upright square lattice and diagonal square lattice; the latter is also called the centered square lattice.. They differ by an angle of 45°. This is related to the fact that a square lattice can be partitioned into two square sub-lattices, as is evident in the colouring of a checkerboard. Symmetry The square lattice's symmetry category is wallpaper group . A pattern with this lattice of translational symmetry cannot have more, but may have less symmetry than the lattice itself. An upright square lattice can be vi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbifold Notation
In geometry, orbifold notation (or orbifold signature) is a system, invented by the mathematician William Thurston and promoted by John Horton Conway, John Conway, for representing types of symmetry groups in two-dimensional spaces of constant curvature. The advantage of the notation is that it describes these groups in a way which indicates many of the groups' properties: in particular, it follows William Thurston in describing the orbifold obtained by taking the quotient of Euclidean space by the group under consideration. Groups representable in this notation include the point groups in three dimensions, point groups on the sphere (S^2), the frieze groups and wallpaper groups of the Euclidean plane (E^2), and their analogues on the hyperbolic geometry, hyperbolic plane (H^2). Definition of the notation The following types of Euclidean transformation can occur in a group described by orbifold notation: * reflection through a line (or plane) * translation by a vector * rotati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point Group
In geometry, a point group is a group (mathematics), mathematical group of symmetry operations (isometry, isometries in a Euclidean space) that have a Fixed point (mathematics), fixed point in common. The Origin (mathematics), coordinate origin of the Euclidean space is conventionally taken to be a fixed point, and every point group in dimension ''d'' is then a subgroup of the orthogonal group O(''d''). Point groups are used to describe the Symmetry (geometry), symmetries of geometric figures and physical objects such as molecular symmetry, molecules. Each point group can be Group representation, represented as sets of orthogonal matrix, orthogonal matrices ''M'' that transform point ''x'' into point ''y'' according to . Each element of a point group is either a Rotation (mathematics), rotation (determinant of ), or it is a Reflection (mathematics), reflection or improper rotation (determinant of ). The geometric symmetries of crystals are described by space groups, which allow T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wallpaper Groups
A wallpaper group (or plane symmetry group or plane crystallographic group) is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art, especially in textiles, tiles, and wallpaper. The simplest wallpaper group, Group ''p''1, applies when there is no symmetry beyond simple translation of a pattern in two dimensions. The following patterns have more forms of symmetry, including some rotational and reflectional symmetries: Image:Wallpaper_group-p4m-2.jpg, Example A: Cloth, Tahiti Image:Wallpaper_group-p4m-1.jpg, Example B: Ornamental painting, Nineveh, Assyria Image:Wallpaper_group-p4g-2.jpg, Example C: Painted porcelain, China Examples A and B have the same wallpaper group; it is called ''p''4''m'' in the IUCr notation and *442 in the orbifold notation. Example C has a different wallpaper group, called ''p''4''g'' or 4*2 . The fact that A and B have the sa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |