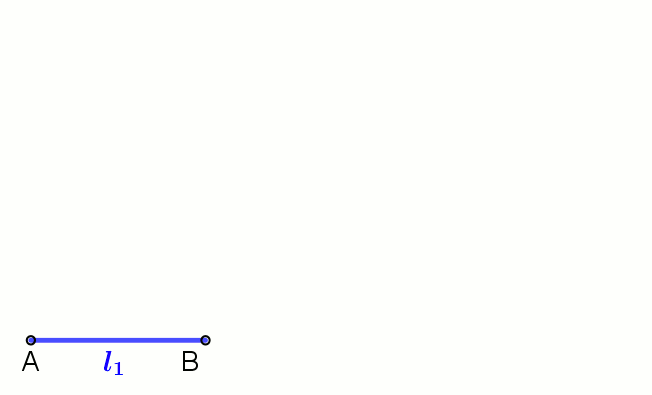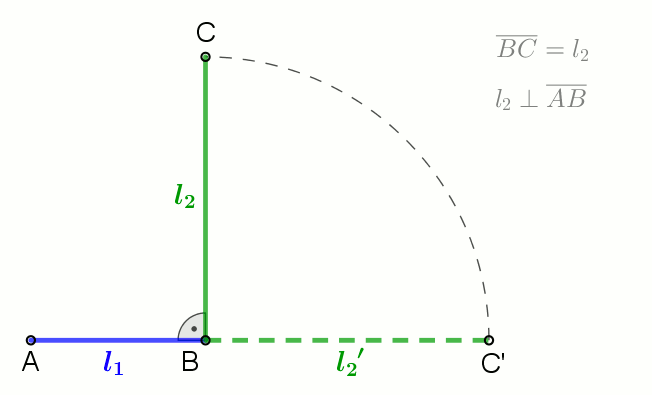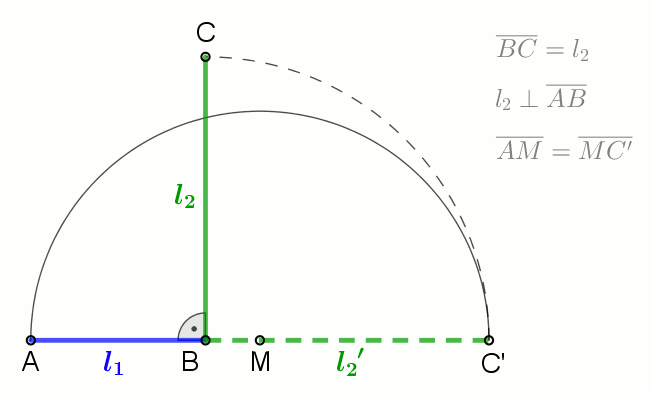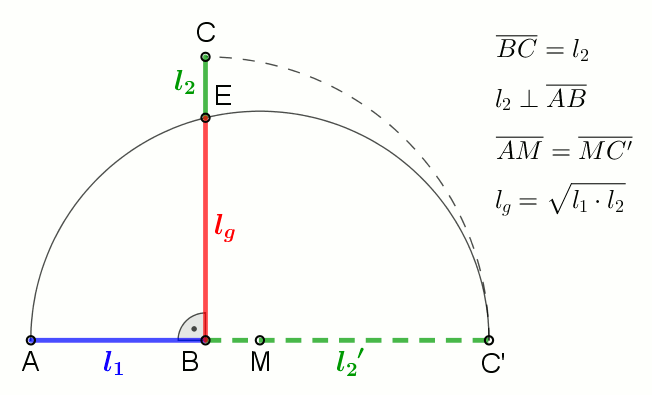|
Heinz Mean
In mathematics, the Heinz mean (named after E. Heinz) of two non-negative real numbers ''A'' and ''B'', was defined by Bhatia as: :\operatorname_x(A, B) = \frac, with 0 ≤ ''x'' ≤ . For different values of ''x'', this Heinz mean interpolates between the arithmetic (''x'' = 0) and geometric Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ca ... (''x'' = 1/2) means such that for 0 < ''x'' < : : The Heinz means appear naturally when symmetrizing -divergences. It may also be defined in the same way for [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erhard Heinz
Erhard Heinz (30 April 1924, Bautzen – 29 December 2017, Göttingen) was a German mathematician known for his work on partial differential equations, in particular the Monge–Ampère equation. He worked as professor in Stanford, Munich and from 1966 until his retirement 1992 at the University of Göttingen. Heinz obtained his PhD in 1951 under the supervision of Franz Rellich at the University of Göttingen. His most important scientific work deals with the existence and regularity theory of systems of non-linear partial differential equations, with applications to differential geometry and mathematical physics. He obtained important results in the theory of surfaces with prescribed mean curvature, in particular of minimal surfaces, for the Weyl embedding problem, and for systems of Monge-Ampère type. In 1994 he was awarded the Cantor medal. His doctoral students include Hans Wilhelm Alt, Wolf von Wahl, Willi Jäger, Helmut Werner, Reinhold Böhme, Friedrich Tomi, and Fri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measurement, measure a ''continuous'' one-dimensional quantity such as a distance, time, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limit (mathematics), limits, continuous function, continuity and derivatives. The set of real numbers is mathematical notation, denoted or \mathbb and is sometimes called "the reals". The adjective ''real'' in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of ), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers subset, include t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Mean
In mathematics and statistics, the arithmetic mean ( ) or arithmetic average, or just the ''mean'' or the '' average'' (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results of an experiment or an observational study, or frequently a set of results from a survey. The term "arithmetic mean" is preferred in some contexts in mathematics and statistics, because it helps distinguish it from other means, such as the geometric mean and the harmonic mean. In addition to mathematics and statistics, the arithmetic mean is used frequently in many diverse fields such as economics, anthropology and history, and it is used in almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation's population. While the arithmetic mean is often used to report central tendencies, it is not a robust statistic, meaning that it is greatly in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the th root of the product of numbers, i.e., for a set of numbers , the geometric mean is defined as :\left(\prod_^n a_i\right)^\frac = \sqrt /math> or, equivalently, as the arithmetic mean in logscale: :\exp For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product, that is, \sqrt = 4. As another example, the geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2, that is, \sqrt = 1/2. The geometric mean applies only to positive numbers. The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as a set of growth figures: values of the human population or int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive Semidefinite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number z^\textsfMz is positive for every nonzero real column vector z, where z^\textsf is the transpose of More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number z^* Mz is positive for every nonzero complex column vector z, where z^* denotes the conjugate transpose of z. Positive semi-definite matrices are defined similarly, except that the scalars z^\textsfMz and z^* Mz are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called indefinite. A matrix is thus positive-definite if and only if it is the matrix of a positive-definite quadratic form or Hermitian form. In other words, a matrix is positive-definite if and only if it defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value ( magnitude and sign) of a given data set. For a data set, the '' arithmetic mean'', also known as "arithmetic average", is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the '' sample mean'' (\bar) to distinguish it from the mean, or expected value, of the underlying distribution, the '' population mean'' (denoted \mu or \mu_x).Underhill, L.G.; Bradfield d. (1998) ''Introstat'', Juta and Company Ltd.p. 181/ref> Outside probability and statistics, a wide range of other notions of m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Muirhead's Inequality
In mathematics, Muirhead's inequality, named after Robert Franklin Muirhead, also known as the "bunching" method, generalizes the inequality of arithmetic and geometric means. Preliminary definitions ''a''-mean For any real vector :a=(a_1,\dots,a_n) define the "''a''-mean" 'a''of positive real numbers ''x''1, ..., ''x''''n'' by : \frac\sum_\sigma x_^\cdots x_^, where the sum extends over all permutations σ of . When the elements of ''a'' are nonnegative integers, the ''a''-mean can be equivalently defined via the monomial symmetric polynomial m_a(x_1,\dots,x_n) as : = \frac m_a(x_1,\dots,x_n), where ℓ is the number of distinct elements in ''a'', and ''k''1, ..., ''k''ℓ are their multiplicities. Notice that the ''a''-mean as defined above only has the usual properties of a mean (e.g., if the mean of equal numbers is equal to them) if a_1+\cdots+a_n=1. In the general case, one can consider instead , which is called a Muirhead mean.Bullen, P. S. Handbook of means and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
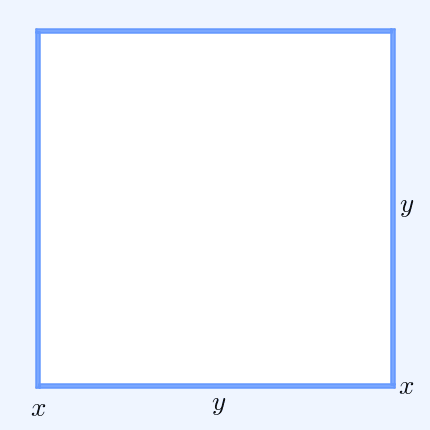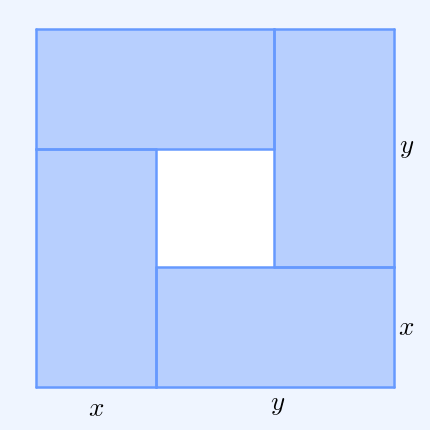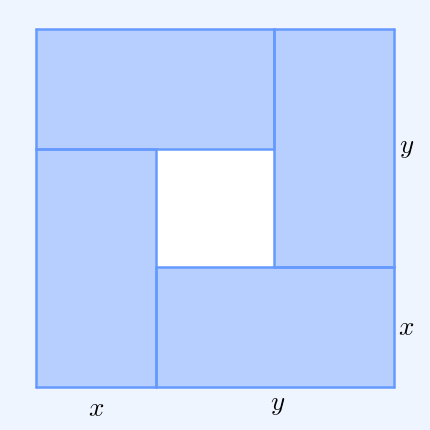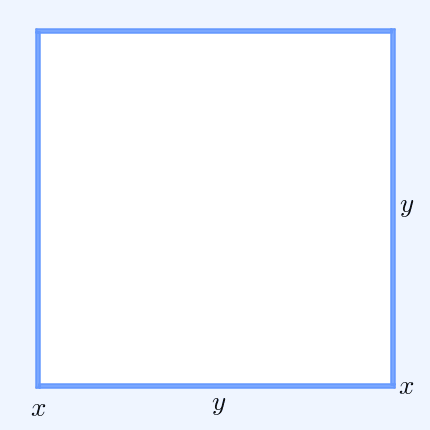
Inequality Of Arithmetic And Geometric Means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if every number in the list is the same (in which case they are both that number). The simplest non-trivial case – i.e., with more than one variable – for two non-negative numbers and , is the statement that :\frac2 \ge \sqrt with equality if and only if . This case can be seen from the fact that the square of a real number is always non-negative (greater than or equal to zero) and from the elementary case of the binomial formula: :\begin 0 & \le (x-y)^2 \\ & = x^2-2xy+y^2 \\ & = x^2+2xy+y^2 - 4xy \\ & = (x+y)^2 - 4xy. \end Hence , with equality precisely when , i.e. . The AM–GM inequality then follows from taking the positive square root of both sides and then dividing both ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |