|
Hannan–Quinn Information Criterion
In statistics, the Hannan–Quinn information criterion (HQC) is a criterion for model selection. It is an alternative to Akaike information criterion (AIC) and Bayesian information criterion (BIC). It is given as : \mathrm = -2 L_ + 2 k \ln(\ln(n))\ Where: * ''L_'' is the log-likelihood, * ''k'' is the number of parameters, and * ''n'' is the number of observations. According to Burnham and Anderson, HQIC, "while often cited, seems to have seen little use in practice" (p. 287). They also note that HQIC, like BIC, but unlike AIC, is not an estimator of Kullback–Leibler divergence. Claeskens and Hjort note that HQC, like BIC, but unlike AIC, is not asymptotically efficient; however, it misses the optimal estimation rate by a very small \ln(\ln(n)) factor (ch. 4). They further point out that whatever method is being used for fine-tuning the criterion will be more important in practice than the term \ln(\ln(n)), since this latter number is small even for very large n; h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Model Selection
Model selection is the task of selecting a model from among various candidates on the basis of performance criterion to choose the best one. In the context of machine learning and more generally statistical analysis, this may be the selection of a statistical model from a set of candidate models, given data. In the simplest cases, a pre-existing set of data is considered. However, the task can also involve the design of experiments such that the data collected is well-suited to the problem of model selection. Given candidate models of similar predictive or explanatory power, the simplest model is most likely to be the best choice (Occam's razor). state, "The majority of the problems in statistical inference can be considered to be problems related to statistical modeling". Relatedly, has said, "How hetranslation from subject-matter problem to statistical model is done is often the most critical part of an analysis". Model selection may also refer to the problem of selecting ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Akaike Information Criterion
The Akaike information criterion (AIC) is an estimator of prediction error and thereby relative quality of statistical models for a given set of data. Given a collection of models for the data, AIC estimates the quality of each model, relative to each of the other models. Thus, AIC provides a means for model selection. AIC is founded on information theory. When a statistical model is used to represent the process that generated the data, the representation will almost never be exact; so some information will be lost by using the model to represent the process. AIC estimates the relative amount of information lost by a given model: the less information a model loses, the higher the quality of that model. In estimating the amount of information lost by a model, AIC deals with the trade-off between the goodness of fit of the model and the simplicity of the model. In other words, AIC deals with both the risk of overfitting and the risk of underfitting. The Akaike information crite ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Information Criterion
In statistics, the Bayesian information criterion (BIC) or Schwarz information criterion (also SIC, SBC, SBIC) is a criterion for model selection among a finite set of models; models with lower BIC are generally preferred. It is based, in part, on the likelihood function and it is closely related to the Akaike information criterion (AIC). When fitting models, it is possible to increase the maximum likelihood by adding parameters, but doing so may result in overfitting. Both BIC and AIC attempt to resolve this problem by introducing a penalty term for the number of parameters in the model; the penalty term is larger in BIC than in AIC for sample sizes greater than 7. The BIC was developed by Gideon E. Schwarz and published in a 1978 paper, as a large-sample approximation to the Bayes factor. Definition The BIC is formally defined as : \mathrm = k\ln(n) - 2\ln(\widehat L). \ where *\hat L = the maximized value of the likelihood function of the model M, i.e. \hat L=p(x\mid\wid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameters
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when identifying the system, or when evaluating its performance, status, condition, etc. ''Parameter'' has more specific meanings within various disciplines, including mathematics, computer programming, engineering, statistics, logic, linguistics, and electronic musical composition. In addition to its technical uses, there are also extended uses, especially in non-scientific contexts, where it is used to mean defining characteristics or boundaries, as in the phrases 'test parameters' or 'game play parameters'. Modelization When a system is modeled by equations, the values that describe the system are called ''parameters''. For example, in mechanics, the masses, the dimensions and shapes (for solid bodies), the densities and the viscosities ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Observations
Observation in the natural sciences is an act or instance of noticing or perceiving and the acquisition of information from a primary source. In living beings, observation employs the senses. In science, observation can also involve the perception and recording of data via the use of scientific instruments. The term may also refer to any data collected during the scientific activity. Observations can be qualitative, that is, the absence or presence of a property is noted and the observed phenomenon described, or quantitative if a numerical value is attached to the observed phenomenon by counting or measuring. Science The scientific method requires observations of natural phenomena to formulate and test hypotheses. It consists of the following steps: # Ask a question about a phenomenon # Make observations of the phenomenon # Formulate a hypothesis that tentatively answers the question # Predict logical, observable consequences of the hypothesis that have not yet been investig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
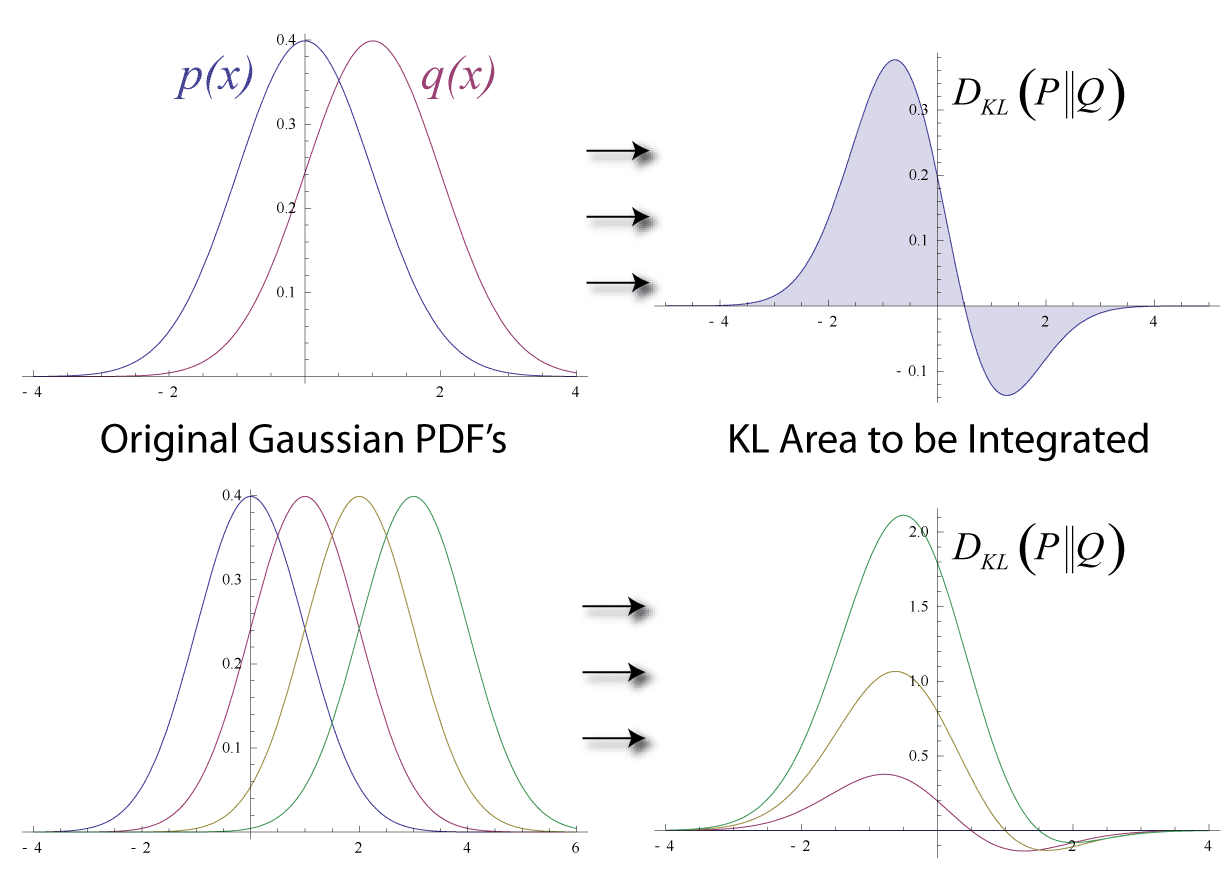
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for cer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gerda Claeskens
Gerda Claeskens is a Belgian statistician. She is a professor of statistics in the Faculty of Economics and Business at KU Leuven, associated with the KU Research Centre for Operations Research and Business Statistics (ORSTAT). Contributions Claeskens is an expert in nonparametric statistics and in model selection, including model averaging. She is known for developing, with Nils Lid Hjort, the focused information criterion for model selection. With Hjort, she is the author of the book ''Model Selection and Model Averaging'' (Cambridge University Press, 2008). Education and career Claeskens earned a licentiate in mathematics at the University of Antwerp in 1995. In 1999, she earned a master's degree in biostatistics and Ph.D. in mathematics, at Limburgs Universitair Centrum (now the University of Hasselt); her dissertation, supervised by Marc Aerts, was ''Smoothing Techniques and Bootstrap Methods for Multiparameter Likelihood''. She did postdoctoral research at the Australian N ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nils Lid Hjort
Nils Lid Hjort (born 12 January 1953) is a Norwegian statistician, who has been a professor of mathematical statistics at the University of Oslo since 1991. Hjort's research themes are varied, with particularly noteworthy contributions in the fields of Bayesian probability (Beta processes for use in non- and semi-parametric models, particularly within survival analysis and event history analysis, but also with links to Indian buffet processes in machine learning), density estimation and nonparametric regression (local likelihood methodology), model selection ( focused information criteria and model averaging), confidence distributions, and change detection. He has also worked with spatial statistics, statistics of remote sensing, pattern recognition, etc. An article on frequentist model averaging, with co-author Gerda Claeskens, was selected as ''Fast Breaking Paper in the field of mathematics'' by the Essential Science Indicators in 2005. This and a companion paper, both publi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Efficiency (statistics)
In statistics, efficiency is a measure of quality of an estimator, of an experimental design, or of a hypothesis testing procedure. Essentially, a more efficient estimator needs fewer input data or observations than a less efficient one to achieve the Cramér–Rao bound. An ''efficient estimator'' is characterized by having the smallest possible variance, indicating that there is a small deviance between the estimated value and the "true" value in the L2 norm sense. The relative efficiency of two procedures is the ratio of their efficiencies, although often this concept is used where the comparison is made between a given procedure and a notional "best possible" procedure. The efficiencies and the relative efficiency of two procedures theoretically depend on the sample size available for the given procedure, but it is often possible to use the asymptotic relative efficiency (defined as the limit of the relative efficiencies as the sample size grows) as the principal comparison ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
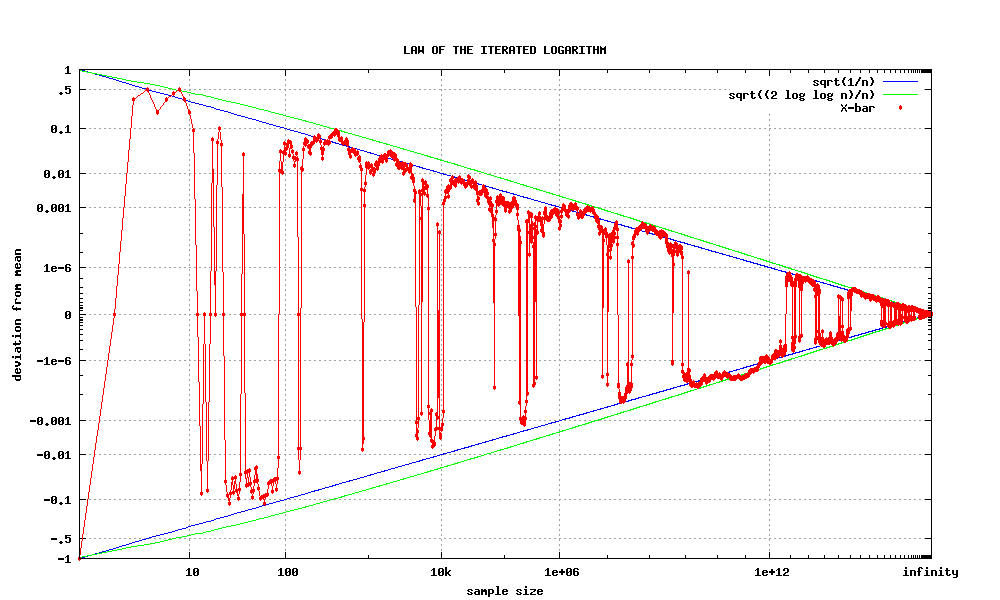
Law Of The Iterated Logarithm
In probability theory, the law of the iterated logarithm describes the magnitude of the fluctuations of a random walk. The original statement of the law of the iterated logarithm is due to Aleksandr Khinchin, A. Ya. Khinchin (1924). Another statement was given by Andrey Kolmogorov, A. N. Kolmogorov in 1929.Andrey Kolmogorov, A. Kolmogoroff"Über das Gesetz des iterierten Logarithmus" ''Mathematische Annalen'', 101: 126–135, 1929. Statement Let be independent, identically distributed random variables with zero means and unit variances. Let ''S''''n'' = ''Y''1 + ... + ''Y''''n''. Then : \limsup_ \frac = 1 \quad \text, where "log" is the natural logarithm, "lim sup" denotes the limit superior, and "a.s." stands for "almost surely". Another statement given by Andrey Kolmogorov, A. N. Kolmogorov in 1929 is as follows. Let \ be independent random variables with zero means and finite variances. Let S_n = Y_1 + \dots + Y_n and B_n = \operatorname(Y_1) + \dots + \operator ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deviance Information Criterion
The deviance information criterion (DIC) is a hierarchical modeling generalization of the Akaike information criterion (AIC). It is particularly useful in Bayesian model selection problems where the posterior distributions of the models have been obtained by Markov chain Monte Carlo (MCMC) simulation. DIC is an asymptotic approximation as the sample size becomes large, like AIC. It is only valid when the posterior distribution is approximately multivariate normal. Definition Define the deviance as D(\theta)=-2 \log(p(y, \theta))+C\, , where y are the data, \theta are the unknown parameters of the model and p(y, \theta) is the likelihood function. C is a constant that cancels out in all calculations that compare different models, and which therefore does not need to be known. There are two calculations in common usage for the effective number of parameters of the model. The first, as described in , is p_D=\overline-D(\bar), where \bar is the expectation of \theta. The second, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |