|
Gregory's Series
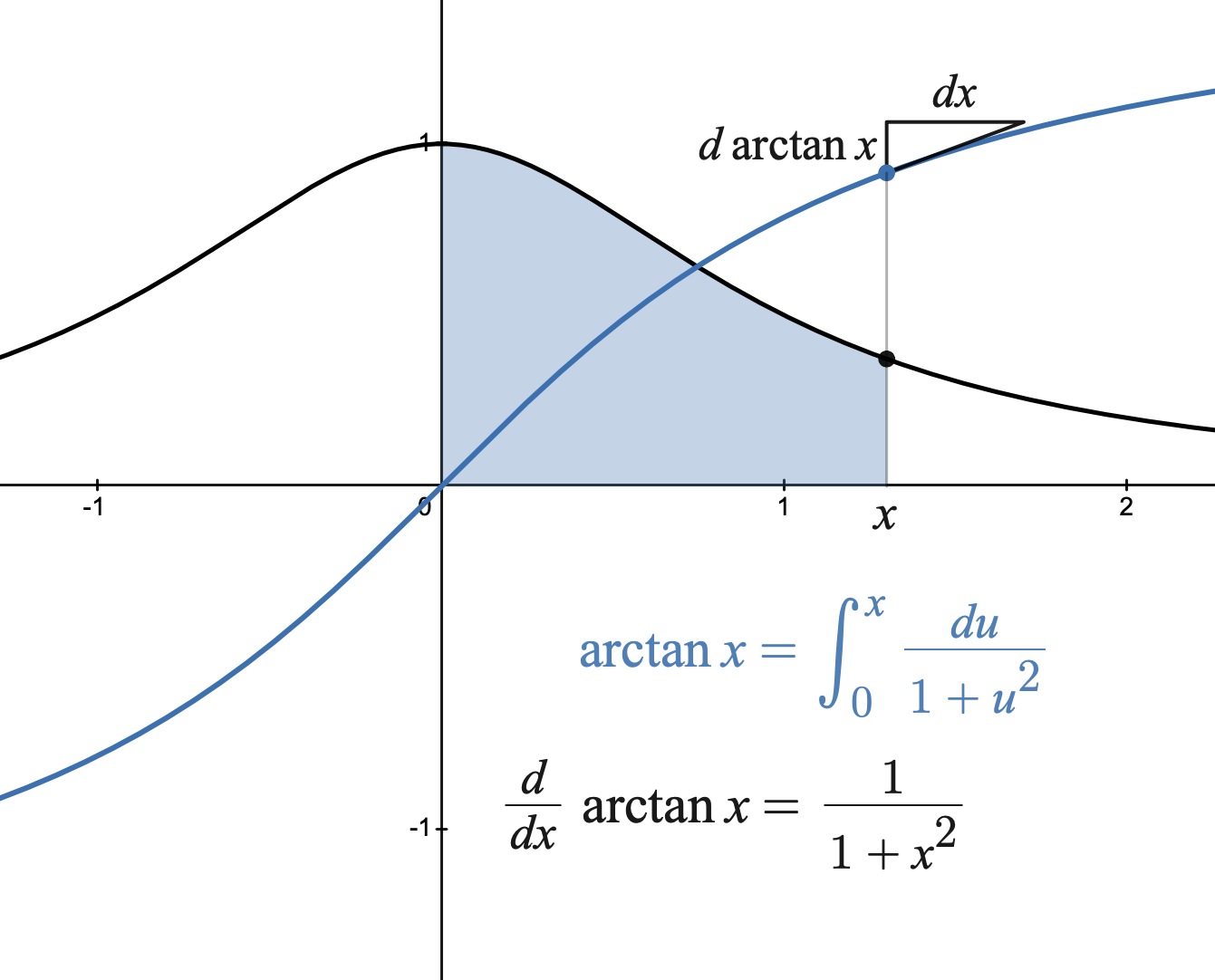
In mathematics, the arctangent series, traditionally called Gregory's series, is the Taylor series expansion at the origin of the arctangent function: :\arctan x = x - \frac + \frac - \frac + \cdots = \sum_^\infty \frac. This series converges in the complex disk , x, \leq 1, except for x = \pm i (where It was first discovered in the 14th century by Indian mathematician Mādhava of Sangamagrāma ( – c. 1425), the founder of the Kerala school, and is described in extant works by Nīlakaṇṭha Somayāji (c. 1500) and Jyeṣṭhadeva (c. 1530). Mādhava's work was unknown in Europe, and the arctangent series was independently rediscovered by James Gregory in 1671 and by Gottfried Leibniz in 1673. In recent literature the arctangent series is sometimes called the Mādhava–Gregory series to recognize Mādhava's priority (see also Mādhava series). The special case of the arctangent of is traditionally called the ''Leibniz formula'' for , or recently sometim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, achieved the Unification of theories in physics#Unification of gravity and astronomy, first great unification in physics and established classical mechanics. Newton also made seminal contributions to optics, and Leibniz–Newton calculus controversy, shares credit with German mathematician Gottfried Wilhelm Leibniz for formulating calculus, infinitesimal calculus, though he developed calculus years before Leibniz. Newton contributed to and refined the scientific method, and his work is considered the most influential in bringing forth modern science. In the , Newton formulated the Newton's laws of motion, laws of motion and Newton's law of universal g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sankara Variyar
Sankara Variyar (; .) was an astronomer-mathematician of the Kerala school of astronomy and mathematics. His family were employed as temple-assistants in the temple at near modern Ottapalam. Mathematical lineage He was taught mainly by Nilakantha Somayaji (1444–1544), the author of the Tantrasamgraha and Jyesthadeva (1500–1575), the author of Yuktibhāṣā. Other teachers of Shankara include Netranarayana, the patron of Nilakantha Somayaji and Chitrabhanu, the author of an astronomical treaties dated to 1530 and a small work with solutions and proofs for algebraic equations. Works The known works of Shankara Variyar are the following: * ''Yukti-dipika'' - an extensive commentary in verse on ''Tantrasamgraha'' based on ''Yuktibhāṣā''. * ''Laghu-vivrti'' - a short commentary in prose on ''Tantrasamgraha''. * '' Kriya-kramakari'' - a lengthy prose commentary on Lilavati of Bhaskara II. * An astronomical commentary dated 1529 CE. * An astronomical handbook completed a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yuktibhāṣā
''Yuktibhāṣā'' (), also known as Gaṇita-yukti-bhāṣā and ( English: ''Compendium of Astronomical Rationale''), is a major treatise on mathematics and astronomy, written by the Indian astronomer Jyesthadeva of the Kerala school of mathematics around 1530. The treatise, written in Malayalam, is a consolidation of the discoveries by Madhava of Sangamagrama, Nilakantha Somayaji, Parameshvara, Jyeshtadeva, Achyuta Pisharati, and other astronomer-mathematicians of the Kerala school. It also exists in a Sanskrit version, with unclear author and date, composed as a rough translation of the Malayalam original. The work contains proofs and derivations of the theorems that it presents. Modern historians used to assert, based on the works of Indian mathematics that first became available, that early Indian scholars in astronomy and computation lacked in proofs, but demonstrates otherwise. Some of its important topics include the infinite series expansions of functions; pow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tantrasaṅgraha
Tantrasamgraha, or Tantrasangraha, (literally, ''A Compilation of the System'') is an important astronomical treatise written by Nilakantha Somayaji, an astronomer/mathematician belonging to the Kerala school of astronomy and mathematics. The treatise was completed in 1501 CE. It consists of 432 verses in Sanskrit divided into eight chapters. Tantrasamgraha had spawned a few commentaries: ''Tantrasamgraha-vyakhya'' of anonymous authorship and ''Yuktibhāṣā'' authored by Jyeshtadeva in about 1550 CE. Tantrasangraha, together with its commentaries, bring forth the depths of the mathematical accomplishments the Kerala school of astronomy and mathematics, in particular the achievements of the remarkable mathematician of the school Sangamagrama Madhava. In his ''Tantrasangraha'', Nilakantha revised Aryabhata's model for the planets Mercury and Venus. According to George G Joseph his equation of the centre for these planets remained the most accurate until the time of Johannes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, called the imaginary axis, is formed by the imaginary numbers. The complex plane allows for a geometric interpretation of complex numbers. Under addition, they add like vector (geometry), vectors. The multiplication of two complex numbers can be expressed more easily in polar coordinates: the magnitude or ' of the product is the product of the two absolute values, or moduli, and the angle or ' of the product is the sum of the two angles, or arguments. In particular, multiplication by a complex number of modulus 1 acts as a rotation. The complex plane is sometimes called the Argand plane or Gauss plane. Notational conventions Complex numbers In complex analysis, the complex numbers are customarily represented by the symbol , which can be sepa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeros And Poles
In complex analysis (a branch of mathematics), a pole is a certain type of singularity of a complex-valued function of a complex variable. It is the simplest type of non- removable singularity of such a function (see essential singularity). Technically, a point is a pole of a function if it is a zero of the function and is holomorphic (i.e. complex differentiable) in some neighbourhood of . A function is meromorphic in an open set if for every point of there is a neighborhood of in which at least one of and is holomorphic. If is meromorphic in , then a zero of is a pole of , and a pole of is a zero of . This induces a duality between ''zeros'' and ''poles'', that is fundamental for the study of meromorphic functions. For example, if a function is meromorphic on the whole complex plane plus the point at infinity, then the sum of the multiplicities of its poles equals the sum of the multiplicities of its zeros. Definitions A function of a complex variable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Function
In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be rational numbers; they may be taken in any field . In this case, one speaks of a rational function and a rational fraction ''over ''. The values of the variables may be taken in any field containing . Then the domain of the function is the set of the values of the variables for which the denominator is not zero, and the codomain is . The set of rational functions over a field is a field, the field of fractions of the ring of the polynomial functions over . Definitions A function f is called a rational function if it can be written in the form : f(x) = \frac where P and Q are polynomial functions of x and Q is not the zero function. The domain of f is the set of all values of x for which the denominator Q(x) is not zero. How ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and Mathematical notation, notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Kingdom of Prussia, Prussia. Euler is credited for popularizing the Greek letter \pi (lowercase Pi (letter), pi) to denote Pi, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeros And Poles
In complex analysis (a branch of mathematics), a pole is a certain type of singularity of a complex-valued function of a complex variable. It is the simplest type of non- removable singularity of such a function (see essential singularity). Technically, a point is a pole of a function if it is a zero of the function and is holomorphic (i.e. complex differentiable) in some neighbourhood of . A function is meromorphic in an open set if for every point of there is a neighborhood of in which at least one of and is holomorphic. If is meromorphic in , then a zero of is a pole of , and a pole of is a zero of . This induces a duality between ''zeros'' and ''poles'', that is fundamental for the study of meromorphic functions. For example, if a function is meromorphic on the whole complex plane plus the point at infinity, then the sum of the multiplicities of its poles equals the sum of the multiplicities of its zeros. Definitions A function of a complex variable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Holomorphic Function
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space . The existence of a complex derivative in a neighbourhood is a very strong condition: It implies that a holomorphic function is infinitely differentiable and locally equal to its own Taylor series (is '' analytic''). Holomorphic functions are the central objects of study in complex analysis. Though the term '' analytic function'' is often used interchangeably with "holomorphic function", the word "analytic" is defined in a broader sense to denote any function (real, complex, or of more general type) that can be written as a convergent power series in a neighbourhood of each point in its domain. That all holomorphic functions are complex analytic functions, and vice versa, is a major theorem in complex analysis. Holomorphic functions are also sometimes referred to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Series
In mathematics, a geometric series is a series (mathematics), series summing the terms of an infinite geometric sequence, in which the ratio of consecutive terms is constant. For example, 1/2 + 1/4 + 1/8 + 1/16 + ⋯, the series \tfrac12 + \tfrac14 + \tfrac18 + \cdots is a geometric series with common ratio , which converges to the sum of . Each term in a geometric series is the geometric mean of the term before it and the term after it, in the same way that each term of an arithmetic series is the arithmetic mean of its neighbors. While Ancient Greek philosophy, Greek philosopher Zeno's paradoxes about time and motion (5th century BCE) have been interpreted as involving geometric series, such series were formally studied and applied a century or two later by Greek mathematics, Greek mathematicians, for example used by Archimedes to Quadrature of the Parabola, calculate the area inside a parabola (3rd century BCE). Today, geometric series are used in mathematical finance, calculati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |