|
Goodman–Nguyen–Van Fraassen Algebra
A standard, Boolean algebra of events is a set of events related to one another by the familiar operations ''and'', ''or'', and ''not''. A conditional event algebra (CEA) contains not just ordinary events but also conditional events, which have the form "if ''A'', then ''B''". The usual purpose of a CEA is to enable the defining of a probability function, ''P'', that satisfies the equation ''P''(if ''A'' then ''B'') = ''P''(''A'' and ''B'') / ''P''(''A''). Motivation In standard probability theory, an event is a set of outcomes, any one of which would be an occurrence of the event. ''P''(''A''), the probability of event ''A'', is the sum of the probabilities of all ''A''-outcomes, ''P''(''B'') is the sum of the probabilities of all ''B''-outcomes, and ''P''(''A'' and ''B'') is the sum of the probabilities of all outcomes that are both ''A''-outcomes and ''B''-outcomes. In other words, ''and'', customarily represented by the logical symbol ∧, is interpreted as set intersection: ''P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boolean Algebra (structure)
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets, or its elements can be viewed as generalized truth values. It is also a special case of a De Morgan algebra and a Kleene algebra (with involution). Every Boolean algebra gives rise to a Boolean ring, and vice versa, with ring multiplication corresponding to conjunction or meet ∧, and ring addition to exclusive disjunction or symmetric difference (not disjunction ∨). However, the theory of Boolean rings has an inherent asymmetry between the two operators, while the axioms and theorems of Boolean algebra express the symmetry of the theory described by the duality principle. __TOC__ History The term "Boolean algebra" honors George Boole (1815–1864), a self-educated Eng ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a σ-algebra that satisfies measure properties such as ''countable additivity''. The difference between a probability measure and the more general notion of measure (which includes concepts like area or volume) is that a probability measure must assign value 1 to the entire space. Intuitively, the additivity property says that the probability assigned to the union of two disjoint (mutually exclusive) events by the measure should be the sum of the probabilities of the events; for example, the value assigned to the outcome "1 or 2" in a throw of a dice should be the sum of the values assigned to the outcomes "1" and "2". Probability measures have applications in diverse fields, from physics to finance and biology. Definition The requirements for a set function \mu to be a probability measure on a σ-algebra are that: * \mu must return results in the unit interval , 1 returning 0 fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Axioms
The standard probability axioms are the foundations of probability theory introduced by Russian mathematician Andrey Kolmogorov in 1933. These axioms remain central and have direct contributions to mathematics, the physical sciences, and real-world probability cases. There are several other (equivalent) approaches to formalising probability. Bayesians will often motivate the Kolmogorov axioms by invoking Cox's theorem or the Dutch book arguments instead. Kolmogorov axioms The assumptions as to setting up the axioms can be summarised as follows: Let (\Omega, F, P) be a measure space with P(E) being the probability of some event E, and P(\Omega) = 1. Then (\Omega, F, P) is a probability space, with sample space \Omega, event space F and probability measure P. First axiom The probability of an event is a non-negative real number: :P(E)\in\mathbb, P(E)\geq 0 \qquad \forall E \in F where F is the event space. It follows (when combined with the second axiom) that P(E) is always ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David Lewis (philosopher)
David Kellogg Lewis (September 28, 1941 – October 14, 2001) was an American philosopher. Lewis taught briefly at UCLA and then at Princeton University from 1970 until his death. He is closely associated with Australia, whose philosophical community he visited almost annually for more than 30 years. Lewis made significant contributions in philosophy of mind, philosophy of probability, epistemology, philosophical logic, aesthetics, philosophy of mathematics, philosophy of time and philosophy of science. In most of these fields he is considered among the most important figures of recent decades. Lewis is most famous for his work in metaphysics, philosophy of language and semantics, in which his books ''On the Plurality of Worlds'' (1986) and ''Counterfactuals'' (1973) are considered classics. His works on the logic and semantics of counterfactual conditionals are broadly used by philosophers and linguists along with a competing account from Robert Stalnaker; together the S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
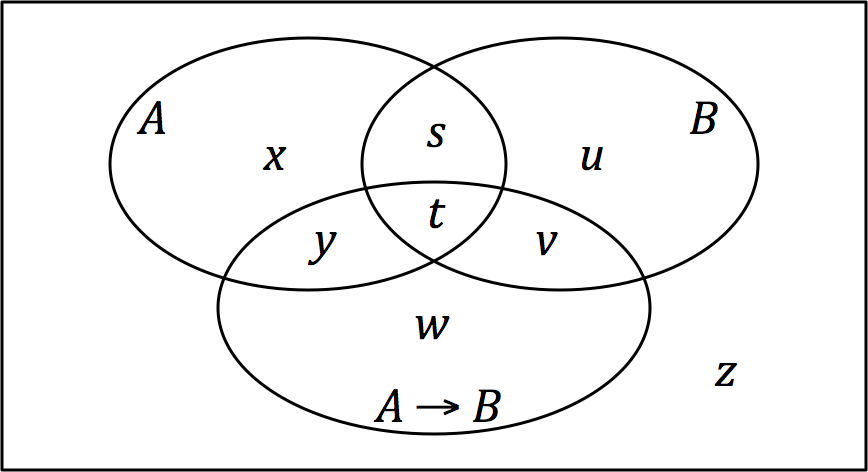
Lewis's Triviality Result
In the mathematical theory of probability, David Lewis's triviality result is a theorem about the impossibility of systematically equating the conditional probability P(B\mid A) with the probability of a so-called conditional event, A \rightarrow B. Conditional probability and conditional events The statement "The probability that if A, then B, is 20%" means (put intuitively) that event B may be expected to occur in 20% of the outcomes where event A occurs. The standard formal expression of this is P(B\mid A)=0.20, where the conditional probability P(B\mid A) equals, by definition, P(A \cap B)/P(A). Beginning in the 1960s, several philosophical logicians—most notably Ernest Adams and Robert Stalnaker—floated the idea that one might also write P(A \rightarrow B) = 0.20, where A \rightarrow B is the conditional event "If A, then B". That is, given events A and B, one might suppose there is an event, A \rightarrow B, such that P(A \rightarrow B) could be counted on to equal P(B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ternary Logic
In logic, a three-valued logic (also trinary logic, trivalent, ternary, or trilean, sometimes abbreviated 3VL) is any of several many-valued logic systems in which there are three truth values indicating ''true'', ''false'' and some indeterminate third value. This is contrasted with the more commonly known bivalent logics (such as classical sentential or Boolean logic) which provide only for ''true'' and ''false''. Emil Leon Post is credited with first introducing additional logical truth degrees in his 1921 theory of elementary propositions. The conceptual form and basic ideas of three-valued logic were initially published by Jan Łukasiewicz and Clarence Irving Lewis. These were then re-formulated by Grigore Constantin Moisil in an axiomatic algebraic form, and also extended to ''n''-valued logics in 1945. Pre-discovery Around 1910, Charles Sanders Peirce defined a many-valued logic system. He never published it. In fact, he did not even number the three pages of notes wher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-valued Logic
In logic, a three-valued logic (also trinary logic, trivalent, ternary, or trilean, sometimes abbreviated 3VL) is any of several many-valued logic systems in which there are three truth values indicating ''true'', ''false'' and some indeterminate third value. This is contrasted with the more commonly known bivalent logics (such as classical sentential or Boolean logic) which provide only for ''true'' and ''false''. Emil Leon Post is credited with first introducing additional logical truth degrees in his 1921 theory of elementary propositions. The conceptual form and basic ideas of three-valued logic were initially published by Jan Łukasiewicz and Clarence Irving Lewis. These were then re-formulated by Grigore Constantin Moisil in an axiomatic algebraic form, and also extended to ''n''-valued logics in 1945. Pre-discovery Around 1910, Charles Sanders Peirce defined a many-valued logic system. He never published it. In fact, he did not even number the three pages of notes whe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distributive Lattice
In mathematics, a distributive lattice is a lattice in which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection. Indeed, these lattices of sets describe the scenery completely: every distributive lattice is—up to isomorphism—given as such a lattice of sets. Definition As in the case of arbitrary lattices, one can choose to consider a distributive lattice ''L'' either as a structure of order theory or of universal algebra. Both views and their mutual correspondence are discussed in the article on lattices. In the present situation, the algebraic description appears to be more convenient. A lattice (''L'',∨,∧) is distributive if the following additional identity holds for all ''x'', ''y'', and ''z'' in ''L'': : ''x'' ∧ (''y'' ∨ ''z'') = (''x'' ∧ ''y'') ∨ (''x'' ∧ ''z''). Viewing lattices as partiall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complemented Lattice
In the mathematical discipline of order theory, a complemented lattice is a bounded lattice (with least element 0 and greatest element 1), in which every element ''a'' has a complement, i.e. an element ''b'' satisfying ''a'' ∨ ''b'' = 1 and ''a'' ∧ ''b'' = 0. Complements need not be unique. A relatively complemented lattice is a lattice such that every interval 'c'', ''d'' viewed as a bounded lattice in its own right, is a complemented lattice. An orthocomplementation on a complemented lattice is an involution that is order-reversing and maps each element to a complement. An orthocomplemented lattice satisfying a weak form of the modular law is called an orthomodular lattice. In bounded distributive lattices, complements are unique. Every complemented distributive lattice has a unique orthocomplementation and is in fact a Boolean algebra. Definition and basic properties A complemented lattice is a bounded lattice (with lea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudocomplement
In mathematics, particularly in order theory, a pseudocomplement is one generalization of the notion of complement. In a lattice ''L'' with bottom element 0, an element ''x'' ∈ ''L'' is said to have a ''pseudocomplement'' if there exists a greatest element ''x''* ∈ ''L'' with the property that ''x'' ∧ ''x''* = 0. More formally, ''x''* = max. The lattice ''L'' itself is called a pseudocomplemented lattice if every element of ''L'' is pseudocomplemented. Every pseudocomplemented lattice is necessarily bounded, i.e. it has a 1 as well. Since the pseudocomplement is unique by definition (if it exists), a pseudocomplemented lattice can be endowed with a unary operation * mapping every element to its pseudocomplement; this structure is sometimes called a ''p''-algebra. However this latter term may have other meanings in other areas of mathematics. Properties In a ''p''-algebra ''L'', for all x, y \in L: * The map ''x'' ↦ ''x''* is antitone. In particular, 0* = 1 and 1* = 0. * T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the mid-18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally better as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |