|
Genus (music)
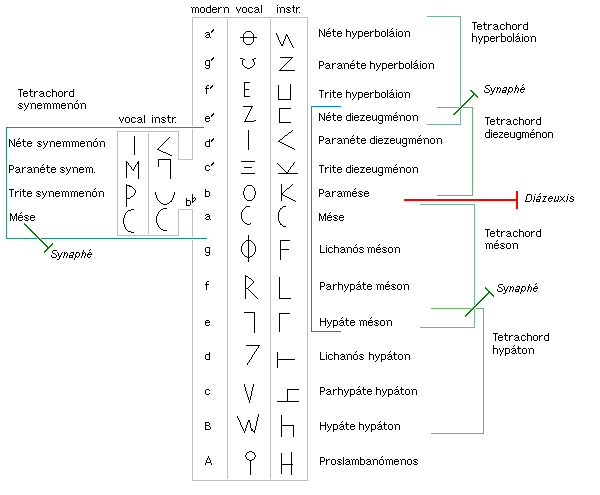
In the musical system of ancient Greece, genus (Greek: γένος 'genos'' pl. γένη 'genē'' Latin: ''genus'', pl. ''genera'' "type, kind") is a term used to describe certain classes of intonations of the two movable notes within a tetrachord. The tetrachordal system was inherited by the Latin medieval theory of scales and by the modal theory of Byzantine music; it may have been one source of the later theory of the jins of Arabic music. In addition, Aristoxenus (in his fragmentary treatise on rhythm) calls some patterns of rhythm "genera". Tetrachords According to the system of Aristoxenus and his followers— Cleonides, Bacchius, Gaudentius, Alypius, Bryennius, and Aristides Quintilianus—the paradigmatic tetrachord was bounded by the fixed tones ''hypate'' and ''mese'', which are a perfect fourth apart and do not vary from one genus to another. Between these are two movable notes, called ''parhypate'' and ''lichanos''. The upper tone, lichanos, can vary over the ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aristoxenus
Aristoxenus of Tarentum (; born 375, fl. 335 BC) was a Ancient Greece, Greek Peripatetic school, Peripatetic philosopher, and a pupil of Aristotle. Most of his writings, which dealt with philosophy, ethics and music, have been lost, but one musical treatise, ''Elements of Harmony'' (Greek: ; Latin: ''Elementa harmonica''), survives incomplete, as well as some fragments concerning rhythm and Metre (music), meter. The ''Elements'' is the chief source of our knowledge of Music of ancient Greece, ancient Greek music. Life Aristoxenus was born at Taranto, Tarentum (in modern-day Apulia, southern Italy) in Magna Graecia, and was the son of a learned musician named Spintharus (otherwise Mnesias). He learned music from his father, and having then been instructed by Lamprus of Erythrae and Xenophilus (philosopher), Xenophilus the Pythagorean, he finally became a pupil of Aristotle, whom he appears to have rivaled in the variety of his studies. According to the ''Suda'', he heaped insults ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical System Of Ancient Greece
The musical system of ancient Greece evolved over a period of more than 500 years from simple scales of tetrachords, or divisions of the perfect fourth, into several complex systems encompassing tetrachords and octaves, as well as octave scales divided into seven to thirteen intervals. Any discussion of the music of ancient Greece, theoretical, philosophical or aesthetic, is fraught with two problems: there are few examples of written music, and there are many, sometimes fragmentary, theoretical and philosophical accounts. The empirical research of scholars like Richard Crocker, C. André Barbera, and John Chalmers has made it possible to look at the ancient Greek systems as a whole without regard to the tastes of any one ancient theorist. The primary genera they examine are those of Pythagoras and the Pythagorean school, Archytas, Aristoxenos, and Ptolemy (including his versions of the genera of Didymus the Musician, Didymos and Eratosthenes). Overview of the first complete to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diatonic Scale
In music theory a diatonic scale is a heptatonic scale, heptatonic (seven-note) scale that includes five whole steps (whole tones) and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps. In other words, the half steps are maximally separated from each other. The seven pitch (music), pitches of any diatonic scale can also be obtained by using a Interval cycle, chain of six perfect fifths. For instance, the seven natural (music), natural pitch classes that form the C-major scale can be obtained from a stack of perfect fifths starting from F: :F–C–G–D–A–E–B. Any sequence of seven successive natural notes, such as C–D–E–F–G–A–B, and any Transposition (music), transposition thereof, is a diatonic scale. Modern musical keyboards are designed so that the white-key notes form a diatonic scale, though transpositions of this diatonic scale require one or more black keys. A diaton ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Tone
Major most commonly refers to: * Major (rank), a military rank * Academic major, an academic discipline to which an undergraduate student formally commits * People named Major, including given names, surnames, nicknames * Major and minor in music, an interval, chord, scale, or key * Major sport competitions Major(s) or The Major may also refer to: Arts and entertainment Fictional characters * Old Major, a pig in ''Animal Farm'' * Major Major Major Major, in ''Catch-22'' * The Major (''Hellsing'') * Major (Cinderella), a horse in Disney's ''Cinderella'' * Major Gowen or the Major, in ''Fawlty Towers'' * Motoko Kusanagi or the Major, in ''Ghost in the Shell'' Film, television, theatre and print * '' The Major'', a 1963 BBC natural history documentary film * ''The Major'' (film), a 2013 Russian action film * ''Major'' (film), a 2022 Indian biopic * ''Major'' (manga), a sports manga and anime series by Takuya Mitsuda * ''The Major'' (play), an 1881 American musical comed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are determined by choosing a sequence of fifthsBruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: McGraw-Hill). Vol. I: p. 56. which are " pure" or perfect, with ratio 3:2. This is chosen because it is the next harmonic of a vibrating string, after the octave (which is the ratio 2:1), and hence is the next most consonant "pure" interval, and the easiest to tune by ear. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2 (i.e., the untempered perfect fifth), which is ≈ 702 cents wide. The system dates back to Ancient Mesopotamia;. (See .) It is named, and has been widely misattributed, to Ancient Greeks, notably Pythagoras (six ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diatonic Tetrachord Pythagorean Tuning
Diatonic and chromatic are terms in music theory that are used to characterize scales. The terms are also applied to musical instruments, intervals, chords, notes, musical styles, and kinds of harmony. They are very often used as a pair, especially when applied to contrasting features of the common practice music of the period 1600–1900. These terms may mean different things in different contexts. Very often, ''diatonic'' refers to musical elements derived from the modes and transpositions of the "white note scale" C–D–E–F–G–A–B. In some usages it includes all forms of heptatonic scale that are in common use in Western music (the major, and all forms of the minor). ''Chromatic'' most often refers to structures derived from the chromatic scale in 12-tone equal temperament, which consists of all semitones. Historically, however, it had other senses, referring in Ancient Greek music theory to a particular tuning of the tetrachord, and to a rhythmic notational con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genesis Of A Music
''Genesis of a Music'' is a book first published in 1949 by microtonal composer Harry Partch (1901–1974). Partch first presents a polemic against both equal temperament and the long history of stagnation in the teaching of music; according to Alex Ross, this is "the most startling forty-five-page history of music ever written". In particular, Partch holds Johann Sebastian Bach responsible for "the movement toward equal-tempered tuning, which meant that composers could not absorb the scales of other world traditions; and the urge to make music ever more instrumental and abstract." He then goes on to explain his tuning theory based on just intonation, the ensemble of musical instruments of his own invention (such as the "Surrogate Kithara, a struck-string, harplike instrument", and the guitar with movable frets he used to compose ''Barstow''), and several of his largest musical compositions. The book has been highly influential to succeeding generations of microtonal compose ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harry Partch
Harry Partch (June 24, 1901 – September 3, 1974) was an American composer, music theorist, and creator of unique musical instruments. He composed using scales of unequal intervals in just intonation, and was one of the first 20th-century composers in the West to work systematically with microtonal scales, alongside Lou Harrison. He built his own instruments in these tunings on which to play his compositions, and described the method behind his theory and practice in his book '' Genesis of a Music'' (1947). Partch composed with scales dividing the octave into 43 unequal tones derived from the natural harmonic series; these scales allowed for more tones of smaller intervals than in standard Western tuning, which uses twelve equal intervals to the octave. To play his music, Partch built many unique instruments, with such names as the Chromelodeon, the Quadrangularis Reversum, and the Zymo-Xyl. Partch described his music as "corporeal" (emphasizing its physical/viscera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George Pachymeres
George Pachymeres (; 1242 – 1310) was a Byzantine Greek historian, philosopher, music theorist and miscellaneous writer. Biography Pachymeres was born at Nicaea, in Bithynia, where his father had taken refuge after the capture of Constantinople by the Latins in 1204. Upon the recovery of Constantinople from the Latin Empire by Michael VIII Palaeologus, Pachymeres settled there, studied law, entered the church, and subsequently became chief advocate of the church and chief justice of the imperial court. His literary activity was considerable, his most important work being a Byzantine history in thirteen books, in continuation of that of George Acropolites from 1261 to 1308, containing the history of the reigns of Michael and Andronicus II Palaeologus. Pachymeres was also the author of rhetorical exercises on philosophical themes; of a ''Quadrivium'' (arithmetic, music, geometry, astronomy), valuable for the history of music and astronomy in the Middle Ages; a general sketch o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Comma
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B, or D and C. It is equal to the frequency ratio = ≈ 1.01364, or about 23.46 cents, roughly a quarter of a semitone (in between 75:74 and 74:73). The comma that musical temperaments often "temper" is the Pythagorean comma. The Pythagorean comma can be also defined as the difference between a Pythagorean apotome and a Pythagorean limma (i.e., between a chromatic and a diatonic semitone, as determined in Pythagorean tuning); the difference between 12 just perfect fifths and seven octaves; or the difference between three Pythagorean ditones and one octave. (This is why the Pythagorean comma is also called a ''ditonic comma''.) The diminished second, in Pythagorean tuning, is defined as the difference between limma and a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ditone
In music, a ditone (, from , "of two tones") is the interval of a major third. The size of a ditone varies according to the sizes of the two tones of which it is compounded. The largest is the Pythagorean ditone, with a ratio of 81:64, also called a comma-redundant major third; the smallest is the interval with a ratio of 100:81, also called a comma-deficient major third. Pythagorean tuning The Pythagorean ditone is the major third in Pythagorean tuning, which has an interval ratio of 81:64, which is 407.82 cents. The Pythagorean ditone is evenly divisible by two major tones (9/8 or 203.91 cents) and is wider than a just major third (5/4, 386.31 cents) by a syntonic comma (81/80, 21.51 cents). Because it is a comma wider than a "perfect" major third of 5:4, it is called a "comma-redundant" interval. "The major third that appears commonly in the ythagoreansystem (C–E, D–F, etc.) is more properly known as the Pythagorean ditone and consists of two major and two minor semi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |