|
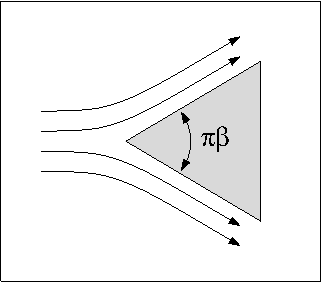
Falkner–Skan Boundary Layer
In fluid dynamics, the Falkner–Skan boundary layer (named after V. M. Falkner and Sylvia W. Skan) describes the steady two-dimensional laminar boundary layer that forms on a wedge, i.e. flows in which the plate is not parallel to the flow. It is also representative of flow on a flat plate with an imposed pressure gradient along the plate length, a situation often encountered in wind tunnel flow. It is a generalization of the flat plate Blasius boundary layer in which the pressure gradient along the plate is zero. Prandtl's boundary layer equations The basis of the Falkner-Skan approach are the Prandtl boundary layer equations. Ludwig Prandtl simplified the equations for fluid flowing along a wall (wedge) by dividing the flow into two areas: one close to the wall dominated by viscosity, and one outside this near-wall boundary layer region where viscosity can be neglected without significant effects on the solution. This means that about half of the terms in the Navier-Stok ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylvia Skan
Sylvia Winifred Skan (15 August 1897 – 10 June 1972) was an English applied mathematician. She is known for her work on aerodynamics, and in particular for the Falkner–Skan boundary layer in the fluid mechanics of airflow past a wedge-shaped obstacle, which she wrote about with V. M. Falkner in 1930, and for the associated Falkner–Skan equation. Skan was born in Bickenhill on 15 August 1897, the oldest of five children of botanist and of his wife Jane Alkins. She does not appear to have earned a university degree. By 1923 she was working for the Aerodynamics Department of the National Physical Laboratory (United Kingdom), National Physical Laboratory, where she carried out the entirety of her career. As well as co-authored research papers, 17 of which listed her as first author, her works included translations of research papers from French, German and Russian into English, and a two-volume single-authored book, ''Handbook for Computers'' (1954), describing the mathematics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reynolds Number
In fluid mechanics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers flows tend to be turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow ( eddy currents). These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation. The Reynolds number has wide applications, ranging from liquid flow in a pipe to the passage of air over an aircraft wing. It is used to predict the transition from laminar to turbulent flow and is used in the scaling of similar but different-sized flow situations, such as between an aircraft model in a wind tunnel and the full-size ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Howarth–Dorodnitsyn Transformation
In fluid dynamics, Howarth–Dorodnitsyn transformation (or Dorodnitsyn-Howarth transformation) is a density-weighted coordinate transformation, which reduces compressible flow conservation equations to simpler form (in most cases, to incompressible form). The transformation was first used by Anatoly Dorodnitsyn in 1942 and later by Leslie Howarth in 1948. The transformation of y coordinate (usually taken as the coordinate normal to the predominant flow direction) to \eta is given by :\eta = \int_0^y \frac \ dy, where \rho is the density and \rho_\infty is the density at infinity. The transformation is extensively used in boundary layer theory and other gas dynamics problems. Stewartson–Illingworth transformation Keith Stewartson and C. R. Illingworth, independently introduced in 1949, a transformation that extends the Howarth–Dorodnitsyn transformation. The transformation reads asN. Curle and HJ Davies: Modern Fluid Dynamics, Vol. 2, Compressible Flow :\xi = \int_0^x \frac\f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prandtl Number
The Prandtl number (Pr) or Prandtl group is a dimensionless number, named after the German physicist Ludwig Prandtl, defined as the ratio of momentum diffusivity to thermal diffusivity. The Prandtl number is given as: : \mathrm = \frac = \frac = \frac = \frac where: * \nu : momentum diffusivity (kinematic viscosity), \nu = \mu/\rho, ( SI units: m2/s) * \alpha : thermal diffusivity, \alpha = k/(\rho c_p), (SI units: m2/s) * \mu : dynamic viscosity, (SI units: Pa s = N s/m2) * k : thermal conductivity, (SI units: W/(m·K)) * c_p : specific heat, (SI units: J/(kg·K)) * \rho : density, (SI units: kg/m3). Note that whereas the Reynolds number and Grashof number are subscripted with a scale variable, the Prandtl number contains no such length scale and is dependent only on the fluid and the fluid state. The Prandtl number is often found in property tables alongside other properties such as viscosity and thermal conductivity. The mass transfer analog of the Prandtl number is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mach Number
Mach number (M or Ma) (; ) is a dimensionless quantity in fluid dynamics representing the ratio of flow velocity past a boundary to the local speed of sound. It is named after the Moravian physicist and philosopher Ernst Mach. : \mathrm = \frac, where: : is the local Mach number, : is the local flow velocity with respect to the boundaries (either internal, such as an object immersed in the flow, or external, like a channel), and : is the speed of sound in the medium, which in air varies with the square root of the thermodynamic temperature. By definition, at Mach1, the local flow velocity is equal to the speed of sound. At Mach0.65, is 65% of the speed of sound (subsonic), and, at Mach1.35, is 35% faster than the speed of sound (supersonic). Pilots of high-altitude aerospace vehicles use flight Mach number to express a vehicle's true airspeed, but the flow field around a vehicle varies in three dimensions, with corresponding variations in local Mach number. The local spe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Enthalpy
Enthalpy , a property of a thermodynamic system, is the sum of the system's internal energy and the product of its pressure and volume. It is a state function used in many measurements in chemical, biological, and physical systems at a constant pressure, which is conveniently provided by the large ambient atmosphere. The pressure–volume term expresses the work (physics), work required to establish the system's physical dimensions, i.e. to make room for it by displacing its surroundings. The pressure-volume term is very small for solids and liquids at common conditions, and fairly small for gases. Therefore, enthalpy is a stand-in for energy in chemical systems; Bond energy, bond, Lattice energy, lattice, solvation and other "energies" in chemistry are actually enthalpy differences. As a state function, enthalpy depends only on the final configuration of internal energy, pressure, and volume, not on the path taken to achieve it. In the International System of Units (SI), the unit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Douglas Hartree
Douglas Rayner Hartree (27 March 1897 – 12 February 1958) was an English mathematician and physicist most famous for the development of numerical analysis and its application to the Hartree–Fock equations of atomic physics and the construction of a differential analyser using Meccano. Early life and education Douglas Hartree was born in Cambridge, England. His father, William, was a lecturer in engineering at the University of Cambridge and his mother, Eva Rayner, was president of the National Council of Women of Great Britain and first woman to be mayor of the city of Cambridge. One of his great-grandfathers was Samuel Smiles; another was the marine engineer William Hartree, partner of John Penn. Douglas Hartree was the oldest of three sons that survived infancy. A brother and sister died in infancy when he was still a child, but his two brothers would later also die. Hartree's 7-year-old brother John Edwin died when Hartree was 17, and Hartree's 22-year-old brot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Layer Separation
In fluid dynamics, flow separation or boundary layer separation is the detachment of a boundary layer from a surface into a wake. A boundary layer exists whenever there is relative movement between a fluid and a solid surface with viscous forces present in the layer of fluid close to the surface. The flow can be externally, around a body, or internally, in an enclosed passage. Boundary layers can be either laminar or turbulent. A reasonable assessment of whether the boundary layer will be laminar or turbulent can be made by calculating the Reynolds number of the local flow conditions. Separation occurs in flow that is slowing down, with pressure increasing, after passing the thickest part of a streamline body or passing through a widening passage, for example. Flowing against an increasing pressure is known as flowing in an adverse pressure gradient. The boundary layer separates when it has travelled far enough in an adverse pressure gradient that the speed of the boundary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stagnation Point Flow
In fluid dynamics, stagnation point flow represents the flow of a fluid in the immediate neighborhood of a stagnation point (or a stagnation line) with which the stagnation point (or the line) is identified for a potential flow or inviscid flow. The flow specifically considers a class of stagnation points known as saddle points where the incoming streamlines gets deflected and directed outwards in a different direction; the streamline deflections are guided by separatrices. The flow in the neighborhood of the stagnation point or line can generally be described using potential flow theory, although viscous effects cannot be neglected if the stagnation point lies on a solid surface. Stagnation point flow without solid surfaces When two streams either of two-dimensional or axisymmetric nature impinge on each other orthogonally, a stagnation plane is created, where the incoming streams are diverted tangentially outwards; thus on the stagnation plane, the velocity component normal to t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Differential Equation
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast with the term partial differential equation which may be with respect to ''more than'' one independent variable. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where , ..., and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of the unknown function of the variable . Among ordinary differential equations, linear differential equations play a prominent role for several reasons. Most elementary and special functions that are encountered in physics and applied mathematics are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Equations (fluid Dynamics)
In fluid dynamics, the Euler equations are a set of quasilinear partial differential equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. In particular, they correspond to the Navier–Stokes equations with zero viscosity and zero thermal conductivity. The Euler equations can be applied to incompressible or compressible flow. The incompressible Euler equations consist of Cauchy equations for conservation of mass and balance of momentum, together with the incompressibility condition that the flow velocity is a solenoidal field. The compressible Euler equations consist of equations for conservation of mass, balance of momentum, and balance of energy, together with a suitable constitutive equation for the specific energy density of the fluid. Historically, only the equations of conservation of mass and balance of momentum were derived by Euler. However, fluid dynamics literature often refers to the full set of the compressible Euler equations – ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.jpg)
.jpg)
