|
Fully Proportional Representation
Fully proportional representation (FPR) is a property of multiwinner voting systems. It extends the property of proportional representation (PR) by requiring that the representation be based on the entire preferences of the voters, rather than on their first choice. Moreover, the requirement combines PR with the requirement of ''accountability'' - each voter knows exactly which elected candidate represents him, and each candidate knows exactly which voters he represents. The term was coined in 1995 by Burt L. Monroe, but a similar idea appeared already in 1983 in a paper by John R. Chamberlin and Paul N. Courant. The two voting rules known to satisfy this property are known - respectively - as Monroe's voting rule and the Chamberlin-Courant (CC) voting rule. Background Most existing electoral systems for proportional representation (PR) are based only on the voters' first preferences, for example: if 40% vote for party A as their first choice, then 40% of the parliament members ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiwinner Voting
Multiwinner or committee voting refers to electoral systems that elect several candidates at once. Such methods can be used to elect parliaments or committees. Goals There are many scenarios in which multiwinner voting is useful. They can be broadly classified into three classes, based on the main objective in electing the committee: # Excellence. Here, voters judge the quality of each candidate individually. The goal is to find the "objectively" best candidates. An example application is shortlisting: selecting, from a list of candidate employees, a small set of finalists, who will proceed to the final stage of evaluation (e.g. using an interview). Here, each candidate is evaluated independently of the others. If two candidates are similar, then probably both will be elected or both will be rejected. # Diversity. Here, the elected candidates should be as ''different'' as possible. For example, suppose the contest is about choosing locations for two fire stations or other fac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Egalitarian Rule
In social choice and operations research, the egalitarian rule (also called the max-min rule or the Rawlsian rule) is a rule saying that, among all possible alternatives, society should pick the alternative which maximizes the ''minimum utility'' of all individuals in society. It is a formal mathematical representation of the egalitarian philosophy. It also corresponds to John Rawls' principle of maximizing the welfare of the worst-off individual. Definition Let X be a set of possible `states of the world' or `alternatives'. Society wishes to choose a single state from X. For example, in a single-winner election, X may represent the set of candidates; in a resource allocation setting, X may represent all possible allocations. Let I be a finite set, representing a collection of individuals. For each i \in I, let u_i:X\longrightarrow\mathbb be a ''utility function'', describing the amount of happiness an individual ''i'' derives from each possible state. A '' social choice rule ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Network Flow Problem
In combinatorial optimization, network flow problems are a class of computational problems in which the input is a flow network (a graph with numerical capacities on its edges), and the goal is to construct a flow, numerical values on each edge that respect the capacity constraints and that have incoming flow equal to outgoing flow at all vertices except for certain designated terminals. Specific types of network flow problems include: *The maximum flow problem, in which the goal is to maximize the total amount of flow out of the source terminals and into the sink terminals *The minimum-cost flow problem, in which the edges have costs as well as capacities and the goal is to achieve a given amount of flow (or a maximum flow) that has the minimum possible cost *The multi-commodity flow problem, in which one must construct multiple flows for different commodities whose total flow amounts together respect the capacities * Nowhere-zero flow, a type of flow studied in combinatorics in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial-time Approximation Scheme
In computer science (particularly algorithmics), a polynomial-time approximation scheme (PTAS) is a type of approximation algorithm for optimization problems (most often, NP-hard optimization problems). A PTAS is an algorithm which takes an instance of an optimization problem and a parameter and produces a solution that is within a factor of being optimal (or for maximization problems). For example, for the Euclidean traveling salesman problem, a PTAS would produce a tour with length at most , with being the length of the shortest tour. Sanjeev Arora, Polynomial-time Approximation Schemes for Euclidean TSP and other Geometric Problems, Journal of the ACM 45(5) 753–782, 1998. The running time of a PTAS is required to be polynomial in the problem size for every fixed ε, but can be different for different ε. Thus an algorithm running in time or even counts as a PTAS. Variants Deterministic A practical problem with PTAS algorithms is that the exponent of the polynomial co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positional Scoring Rule
Positional notation, also known as place-value notation, positional numeral system, or simply place value, usually denotes the extension to any base of the Hindu–Arabic numeral system (or decimal system). More generally, a positional system is a numeral system in which the contribution of a digit to the value of a number is the value of the digit multiplied by a factor determined by the position of the digit. In early numeral systems, such as Roman numerals, a digit has only one value: I means one, X means ten and C a hundred (however, the values may be modified when combined). In modern positional systems, such as the decimal system, the position of the digit means that its value must be multiplied by some value: in 555, the three identical symbols represent five hundreds, five tens, and five units, respectively, due to their different positions in the digit string. The Babylonian numeral system, base 60, was the first positional system to be developed, and its influence is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hardness Of Approximation
In computer science, hardness of approximation is a field that studies the algorithmic complexity of finding near-optimal solutions to optimization problems. Scope Hardness of approximation complements the study of approximation algorithms by proving, for certain problems, a limit on the factors with which their solution can be efficiently approximated. Typically such limits show a factor of approximation beyond which a problem becomes NP-hard, implying that finding a polynomial time approximation for the problem is impossible unless NP=P. Some hardness of approximation results, however, are based on other hypotheses, a notable one among which is the unique games conjecture. History Since the early 1970s it was known that many optimization problems could not be solved in polynomial time unless P = NP, but in many of these problems the optimal solution could be efficiently approximated to a certain degree. In the 1970s, Teofilo F. Gonzalez and Sartaj Sahni began the study of hard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation Algorithms
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems (in particular NP-hard problems) with provable guarantees on the distance of the returned solution to the optimal one. Approximation algorithms naturally arise in the field of theoretical computer science as a consequence of the widely believed P ≠ NP conjecture. Under this conjecture, a wide class of optimization problems cannot be solved exactly in polynomial time. The field of approximation algorithms, therefore, tries to understand how closely it is possible to approximate optimal solutions to such problems in polynomial time. In an overwhelming majority of the cases, the guarantee of such algorithms is a multiplicative one expressed as an approximation ratio or approximation factor i.e., the optimal solution is always guaranteed to be within a (predetermined) multiplicative factor of the returned solution. However, there a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greedy Algorithm
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time. For example, a greedy strategy for the travelling salesman problem (which is of high computational complexity) is the following heuristic: "At each step of the journey, visit the nearest unvisited city." This heuristic does not intend to find the best solution, but it terminates in a reasonable number of steps; finding an optimal solution to such a complex problem typically requires unreasonably many steps. In mathematical optimization, greedy algorithms optimally solve combinatorial problems having the properties of matroids and give constant-factor approximations to optimization problems with the submodular structure. Specifics Greedy algori ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single-crossing Preferences
In monotone comparative statics, the single-crossing condition or single-crossing property refers to a condition where the relationship between two or more functionsThe property need not only relate to continuous functions but can also similarly describe ordered sets or lattices. is such that they will only cross once. For example, a mean-preserving spread will result in an altered probability distribution whose cumulative distribution function will intersect with the original's only once. The single-crossing condition was posited in Samuel Karlin's 1968 monograph 'Total Positivity'. It was later used by Peter Diamond, Joseph Stiglitz, and Susan Athey, in studying the economics of uncertainty. The single-crossing condition is also used in applications where there are a few agents or types of agents that have preferences over an ordered set. Such situations appear often in information economics, contract theory, social choice and political economics, among other fields. Exampl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
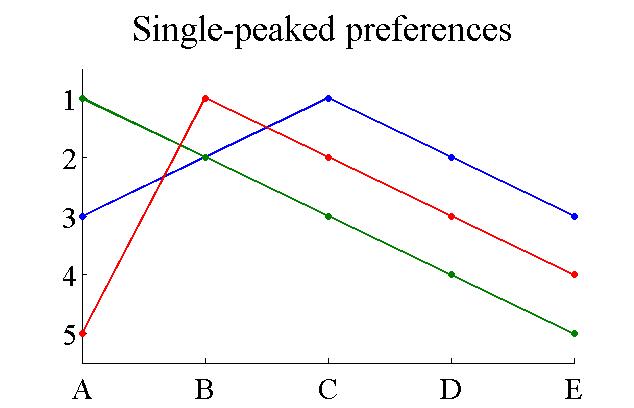
Single-peaked Preferences
Single-peaked preferences are a class of preference relations. A group has single-peaked preferences over a set of outcomes if the outcomes can be ordered along a line such that: # Each agent has a "best outcome" in the set, and # For each agent, outcomes that are further from his or her best outcome are preferred less. Single-peaked preferences are typical of one-dimensional domains. A typical example is when several consumers have to decide on the amount of public good to purchase. The amount is a one-dimensional variable. Usually, each consumer decides on a certain quantity which is best for him or her, and if the actual quantity is more/less than that ideal quantity, the agent is then less satisfied. With single-peaked preferences, there is a simple truthful mechanism for selecting an outcome, which is to select the median quantity; this results in the median voter theorem. It is truthful because the median function satisfies the strong monotonicity property. The notion wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameterized Complexity
In computer science, parameterized complexity is a branch of computational complexity theory that focuses on classifying computational problems according to their inherent difficulty with respect to ''multiple'' parameters of the input or output. The complexity of a problem is then measured as a function of those parameters. This allows the classification of NP-hard problems on a finer scale than in the classical setting, where the complexity of a problem is only measured as a function of the number of bits in the input. This appears to have been first demonstrated in . The first systematic work on parameterized complexity was done by . Under the assumption that P ≠ NP, there exist many natural problems that require super-polynomial running time when complexity is measured in terms of the input size only but that are computable in a time that is polynomial in the input size and exponential or worse in a parameter . Hence, if is fixed at a small value and the growth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approval Ballot
An approval ballot, also called an unordered ballot, is a ballot in which a voter may vote for any number of candidates simultaneously, rather than for just one candidate. Candidates that are selected in a voter's ballot are said to be ''approved'' by the voter; the other candidates are said to be ''disapproved'' or ''rejected''. Approval ballots do not let the voters specify a preference-order among the candidates they approve; hence the name ''unordered''. This is in contrast to ranked ballots, which are ordered. There are several electoral systems that use approval balloting; they differ in the way in which the election outcome is determined: * In approval voting, there is a single winner, and he/she is the candidate with the largest number of votes. * In multiple non-transferable vote (also called block voting) there is a fixed number (say ''k'') of winners, and they are the ''k'' candidates with the largest number of votes. * In other multiwinner approval voting systems, there i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |