|
Frequency Response (electrical Grid)
In signal processing and electronics, the frequency response of a system is the quantitative measure of the magnitude and phase of the output as a function of input frequency. The frequency response is widely used in the design and analysis of systems, such as audio and control systems, where they simplify mathematical analysis by converting governing differential equations into algebraic equations. In an audio system, it may be used to minimize audible distortion by designing components (such as microphones, amplifiers and loudspeakers) so that the overall response is as flat (uniform) as possible across the system's bandwidth. In control systems, such as a vehicle's cruise control, it may be used to assess system stability, often through the use of Bode plots. Systems with a specific frequency response can be designed using analog and digital filters. The frequency response characterizes systems in the frequency domain, just as the impulse response characterizes systems in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Circuit
An electrical network is an interconnection of electrical components (e.g., battery (electricity), batteries, resistors, inductors, capacitors, switches, transistors) or a model of such an interconnection, consisting of electrical elements (e.g., voltage sources, current sources, Electrical resistance and conductance, resistances, inductances, capacitances). An electrical circuit is a network consisting of a closed loop, giving a return path for the current. Thus all circuits are networks, but not all networks are circuits (although networks without a closed loop are often referred to as "open circuits"). A resistive network is a network containing only resistors and ideal current and voltage sources. Network analysis (electrical circuits), Analysis of resistive networks is less complicated than analysis of networks containing capacitors and inductors. If the sources are constant (Direct current, DC) sources, the result is a DC network. The effective resistance and current dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analog Filter
Analogue Filter (signal processing), filters are a basic building block of signal processing much used in electronics. Amongst their many applications are the separation of an audio signal before application to bass (music), bass, mid-range speaker, mid-range, and tweeter loudspeakers; the combining and later separation of multiple telephone conversations onto a single channel; the selection of a chosen radio station in a radio receiver and rejection of others. Passive linear electronic analogue filters are those filters which can be described with linear differential equations (linear); they are composed of capacitors, inductors and, sometimes, resistors (passive component, passive) and are designed to operate on continuously varying analogue signals. There are many linear filters which are not analogue in implementation (digital filter), and there are many electronic filters which may not have a passive topology – both of which may have the same transfer function of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fast Fourier Transform
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). A Fourier transform converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa. The DFT is obtained by decomposing a sequence of values into components of different frequencies. This operation is useful in many fields, but computing it directly from the definition is often too slow to be practical. An FFT rapidly computes such transformations by Matrix decomposition, factorizing the DFT matrix into a product of Sparse matrix, sparse (mostly zero) factors. As a result, it manages to reduce the Computational complexity theory, complexity of computing the DFT from O(n^2), which arises if one simply applies the definition of DFT, to O(n \log n), where is the data size. The difference in speed can be enormous, especially for long data sets where may be in the thousands or millions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Spectrum
In signal processing, the power spectrum S_(f) of a continuous time signal x(t) describes the distribution of power into frequency components f composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, or a spectrum of frequencies over a continuous range. The statistical average of any sort of signal (including noise) as analyzed in terms of its frequency content, is called its spectrum. When the energy of the signal is concentrated around a finite time interval, especially if its total energy is finite, one may compute the energy spectral density. More commonly used is the power spectral density (PSD, or simply power spectrum), which applies to signals existing over ''all'' time, or over a time period large enough (especially in relation to the duration of a measurement) that it could as well have been over an infinite time interval. The PSD then refers to the spectral energy distribution that would b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Butterworth Response
The Butterworth filter is a type of filter (signal processing), signal processing filter designed to have a frequency response that is as flat as possible in the passband. It is also referred to as a maximally flat magnitude filter. It was first described in 1930 by the British engineer and physicist Stephen Butterworth in his paper entitled "On the Theory of Filter Amplifiers". Original paper Butterworth had a reputation for solving very complex mathematical problems thought to be 'impossible'. At the time, filter design required a considerable amount of designer experience due to limitations of the image parameter filter, theory then in use. The filter was not in common use for over 30 years after its publication. Butterworth stated that: Such an ideal filter cannot be achieved, but Butterworth showed that successively closer approximations were obtained with increasing numbers of filter elements of the right values. At the time, filters generated substantial ripple in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Transform
In mathematics, the Laplace transform, named after Pierre-Simon Laplace (), is an integral transform that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a function of a Complex number, complex variable s (in the complex-valued frequency domain, also known as ''s''-domain, or ''s''-plane). The transform is useful for converting derivative, differentiation and integral, integration in the time domain into much easier multiplication and Division (mathematics), division in the Laplace domain (analogous to how logarithms are useful for simplifying multiplication and division into addition and subtraction). This gives the transform many applications in science and engineering, mostly as a tool for solving linear differential equations and dynamical systems by simplifying ordinary differential equations and integral equations into algebraic equation, algebraic polynomial equations, and by simplifyin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transfer Function
In engineering, a transfer function (also known as system function or network function) of a system, sub-system, or component is a function (mathematics), mathematical function that mathematical model, models the system's output for each possible input. It is widely used in electronic engineering tools like Electronic circuit simulation, circuit simulators and control systems. In simple cases, this function can be represented as a two-dimensional graph (function), graph of an independent scalar (mathematics), scalar input versus the dependent scalar output (known as a transfer curve or characteristic curve). Transfer functions for components are used to design and analyze systems assembled from components, particularly using the block diagram technique, in electronics and control theory. Dimensions and units of the transfer function model the output response of the device for a range of possible inputs. The transfer function of a two-port electronic circuit, such as an amplifier, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The term ''convolution'' refers to both the resulting function and to the process of computing it. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result (see #Properties, commutativity). Graphically, it expresses how the 'shape' of one function is modified by the other. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution f*g differs from cross-correlation f \star g only in that either f(x) or g(x) is reflected about the y-axis in convolution; thus i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multistage Amplifier
A multistage amplifier is an electronic amplifier consisting of two or more single-stage amplifiers connected together. In this context, a single stage is an amplifier containing only a single transistor (sometimes a pair of transistors) or other active device. The most common reason for using multiple stages is to increase the gain of the amplifier in applications where the input signal is very small, for instance in radio receivers. In these applications a single stage has insufficient gain by itself. In some designs it is possible to obtain more desirable values of other parameters such as input resistance and output resistance. Connection schemes The simplest, and most common, connection scheme is a cascade connection of identical, or similar, stages forming a cascade amplifier. In a cascade connection, the output port of one stage is connected to the input port of the next. Typically, the individual stages are bipolar junction transistors (BJTs) in a common emit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the transform is a complex-valued function of frequency. The term ''Fourier transform'' refers to both this complex-valued function and the mathematical operation. When a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The Fourier transform is analogous to decomposing the sound of a musical chord into the intensities of its constituent pitches. Functions that are localized in the time domain have Fourier transforms that are spread out across the frequency domain and vice versa, a phenomenon known as the uncertainty principle. The critical case for this principle is the Gaussian function, of substantial importance in probability theory and statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
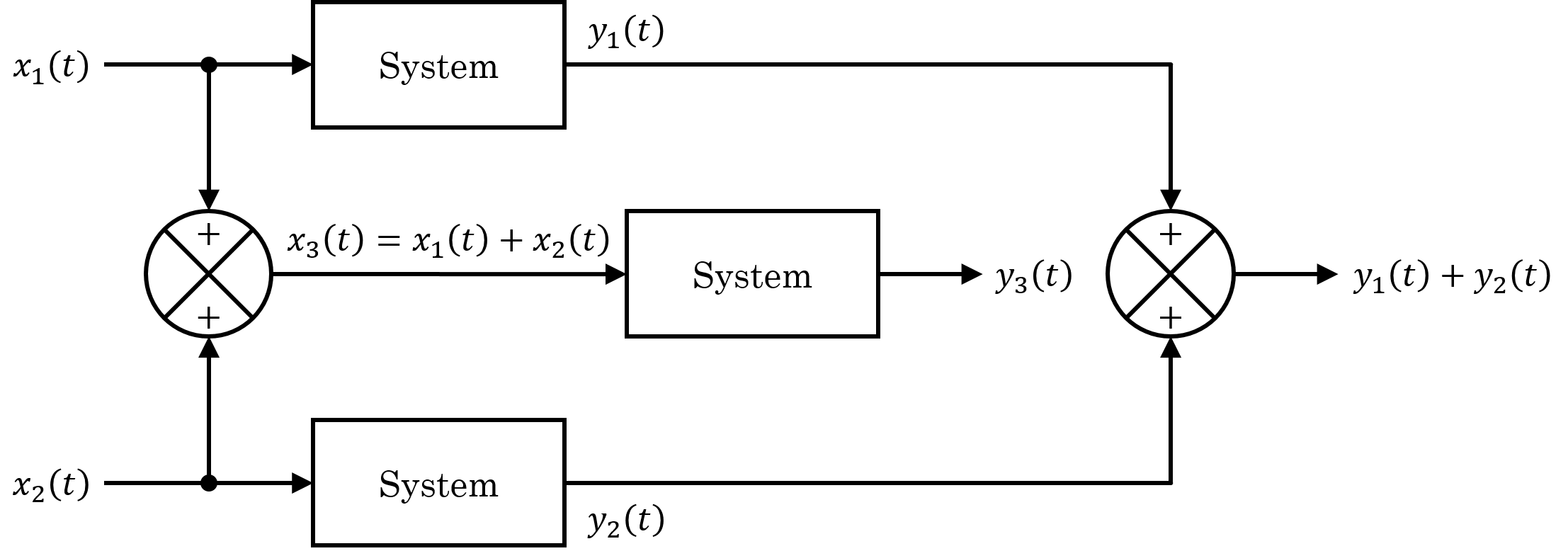
Linear System
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems. Definition A general deterministic system can be described by an operator, , that maps an input, , as a function of to an output, , a type of black box description. A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.) The superposition principle means that a linear combination of inputs to the system produces a linear com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Domain
In mathematics and signal processing, the time domain is a representation of how a signal, function, or data set varies with time. It is used for the analysis of mathematical functions, physical signals or time series of economic or environmental data. In the time domain, the independent variable is time, and the dependent variable is the value of the signal. This contrasts with the frequency domain, where the signal is represented by its constituent frequencies. For continuous-time signals, the value of the signal is defined for all real numbers representing time. For discrete-time signals, the value is known at discrete, often equally-spaced, time intervals. It is commonly visualized using a graph where the x-axis represents time and the y-axis represents the signal's value. An oscilloscope is a common tool used to visualize real-world signals in the time domain. Though most precisely referring to time in physics, the term ''time domain'' may occasionally informally ref ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |