|
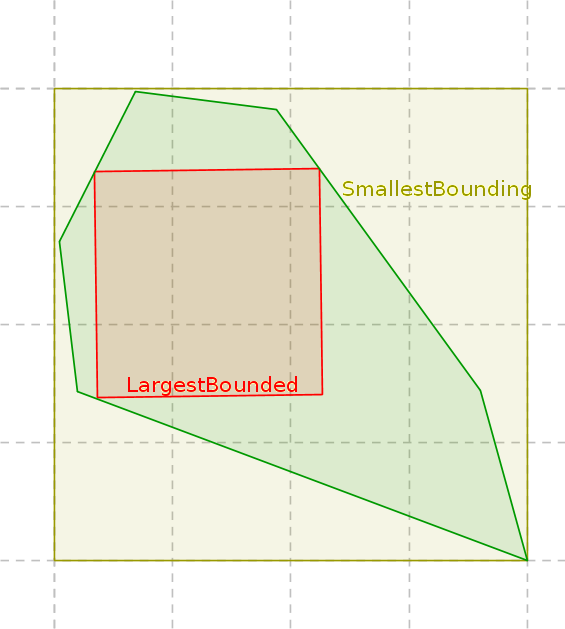
Fat Object (geometry)
In geometry, a fat object is an object in two or more dimensions, whose lengths in the different dimensions are similar. For example, a square is fat because its length and width are identical. A 2-by-1 rectangle is thinner than a square, but it is fat relative to a 10-by-1 rectangle. Similarly, a circle is fatter than a 1-by-10 ellipse and an equilateral triangle is fatter than a very obtuse triangle. Fat objects are especially important in computational geometry. Many algorithms in computational geometry can perform much better if their input consists of only fat objects; see the #Applications, applications section below. Global fatness Given a constant , an object is called -fat if its "slimness factor" is at most . The "slimness factor" has different definitions in different papers. A common definition is: :\frac where and the cubes are -dimensional. A 2-dimensional cube is a square, so the slimness factor of a square is 1 (since its smallest enclosing square is the sam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-ellipse
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0 (the limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but for its perimeter (also known as circumference), integration is required to obtain an exact solution. The largest and smallest diameters of an ellipse, also known as its width and height, are typically denoted and . An ellipse has four extreme points: two '' vertices'' at the endpoints of the major axis and two ''co-vertices'' at the endpoints of the minor axis. Analytically, the equation of a standard ellipse centered at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small-angle Approximation
For small angles, the trigonometric functions sine, cosine, and tangent can be calculated with reasonable accuracy by the following simple approximations: : \begin \sin \theta &\approx \tan \theta \approx \theta, \\ mu\cos \theta &\approx 1 - \tfrac12\theta^2 \approx 1, \end provided the angle is measured in radians. Angles measured in degrees must first be converted to radians by multiplying them by . These approximations have a wide range of uses in branches of physics and engineering, including mechanics, electromagnetism, optics, cartography, astronomy, and computer science. One reason for this is that they can greatly simplify differential equations that do not need to be answered with absolute precision. There are a number of ways to demonstrate the validity of the small-angle approximations. The most direct method is to truncate the Maclaurin series for each of the trigonometric functions. Depending on the order of the approximation, \textstyle \cos \theta is approxi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isosceles Triangle
In geometry, an isosceles triangle () is a triangle that has two Edge (geometry), sides of equal length and two angles of equal measure. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the Golden triangle (mathematics), golden triangle, and the faces of bipyramids and certain Catalan solids. The mathematical study of isosceles triangles dates back to ancient Egyptian mathematics and Babylonian mathematics. Isosceles triangles have been used as decoration from even earlier times, and appear frequently in architecture and design, for instance in the pediments and gables of buildings. The two equal sides are called the ''legs'' and the third side is called the base (geometry), ''base'' of the triangle. The other dimensions of the triangle, such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Law Of Sines
In trigonometry, the law of sines (sometimes called the sine formula or sine rule) is a mathematical equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law, \frac \,=\, \frac \,=\, \frac \,=\, 2R, where , and are the lengths of the sides of a triangle, and , and are the opposite angles (see figure 2), while is the radius of the triangle's circumcircle. When the last part of the equation is not used, the law is sometimes stated using the Multiplicative inverse, reciprocals; \frac \,=\, \frac \,=\, \frac. The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known—a technique known as triangulation. It can also be used when two sides and one of the non-enclosed angles are known. In some such cases, the triangle is not uniquely determined by this data (called the ''ambiguous case'') and the technique gives two possible values for the enclosed angle. The law of sines is on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Triangle
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle ( turn or 90 degrees). The side opposite to the right angle is called the '' hypotenuse'' (side c in the figure). The sides adjacent to the right angle are called ''legs'' (or ''catheti'', singular: '' cathetus''). Side a may be identified as the side ''adjacent'' to angle B and ''opposite'' (or ''opposed to'') angle A, while side b is the side adjacent to angle A and opposite angle B. Every right triangle is half of a rectangle which has been divided along its diagonal. When the rectangle is a square, its right-triangular half is isosceles, with two congruent sides and two congruent angles. When the rectangle is not a square, its right-triangular half is scalene. Every triangle whose base is the diameter of a circle and whose apex lies on the circle is a right triangle, with the right angle at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle (180 degrees or π radians). The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the ''base'', in which case the opposite vertex is called the ''apex''; the shortest segment between the base and apex is the ''height''. The area of a triangle equals one-half the product of height and base length. In Euclidean geometry, any two points determine a unique line segment situated within a unique straight line, and any three points that do not all lie on the same straight line determine a unique triangle situated w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circumscribed Circle
In geometry, a circumscribed circle for a set of points is a circle passing through each of them. Such a circle is said to ''circumscribe'' the points or a polygon formed from them; such a polygon is said to be ''inscribed'' in the circle. * Circumcircle, the circumscribed circle of a triangle, which always exists for a given triangle. * Cyclic polygon, a general polygon that can be circumscribed by a circle. The vertices of this polygon are concyclic points. All triangles are cyclic polygons. * Cyclic quadrilateral, a special case of a cyclic polygon. See also * Smallest-circle problem, the related problem of finding the circle with minimal radius containing an arbitrary set of points, not necessarily passing through them. * Inscribed figure {{sia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete & Computational Geometry
'' Discrete & Computational Geometry'' is a peer-reviewed mathematics journal published quarterly by Springer. Founded in 1986 by Jacob E. Goodman and Richard M. Pollack, the journal publishes articles on discrete geometry and computational geometry. Abstracting and indexing The journal is indexed in: * ''Mathematical Reviews'' * '' Zentralblatt MATH'' * ''Science Citation Index'' * ''Current Contents ''Current Contents'' is a rapid alerting service database from Clarivate, formerly the Institute for Scientific Information and Thomson Reuters. It is published online and in several different printed subject sections. History ''Current Contents ...'' Notable articles Two articles published in ''Discrete & Computational Geometry'', one by Gil Kalai in 1992 with a proof of a subexponential upper bound on the diameter of a polytope and another by Samuel Ferguson in 2006 on the Kepler conjecture on optimal three-dimensional sphere packing, earned their authors the Fulk ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circumcircle
In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertex (geometry), vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcenter is the point of intersection (geometry), intersection between the three perpendicular bisectors of the triangle's sides, and is a triangle center. More generally, an -sided polygon with all its vertices on the same circle, also called the circumscribed circle, is called a cyclic polygon, or in the special case , a cyclic quadrilateral. All rectangles, isosceles trapezoids, right kites, and regular polygons are cyclic, but not every polygon is. Straightedge and compass construction The circumcenter of a triangle can be Compass-and-straightedge construction, constructed by drawing any two of the three Bisection#Perpendicular bisectors, perpendicular bisectors. For three non-collinear points, these two lines cannot be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acute Triangle
An acute triangle (or acute-angled triangle) is a triangle with three ''acute angles'' (less than 90°). An obtuse triangle (or obtuse-angled triangle) is a triangle with one ''obtuse angle'' (greater than 90°) and two acute angles. Since a triangle's angles must sum to 180° in Euclidean geometry, no Euclidean triangle can have more than one obtuse angle. Acute and obtuse triangles are the two different types of oblique triangles—triangles that are not right triangles because they do not have any right angles (90°). Properties In all triangles, the centroid—the intersection of the median (geometry), medians, each of which connects a vertex with the midpoint of the opposite side—and the incenter—the center of the circle that is internally tangent to all three sides—are in the interior of the triangle. However, while the orthocenter and the circumcenter are in an acute triangle's interior, they are exterior to an obtuse triangle. The orthocenter is the in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |