|
Euler–Rodrigues Formula
In mathematics and mechanics, the Euler–Rodrigues formula describes the rotation of a vector in three dimensions. It is based on Rodrigues' rotation formula, but uses a different parametrization. The rotation is described by four Euler parameters due to Leonhard Euler. The Rodrigues formula (named after Olinde Rodrigues), a method of calculating the position of a rotated point, is used in some software applications, such as flight simulators and computer games. Definition A rotation about the origin is represented by four real numbers, , , , such that :a^2 + b^2 + c^2 + d^2 = 1. When the rotation is applied, a point at position rotates to its new position :\vec x' = \begin a^2+b^2-c^2-d^2 & 2(bc-ad) & 2(bd + ac) \\ 2(bc+ad) & a^2+c^2-b^2-d^2 & 2(cd - ab) \\ 2(bd-ac) & 2(cd+ab) & a^2+d^2-b^2-c^2 \end\vec x. Vector formulation The parameter may be called the ''scalar'' parameter and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pauli Spin Matrix
In mathematical physics and mathematics, the Pauli matrices are a set of three complex matrices which are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma (), they are occasionally denoted by tau () when used in connection with isospin symmetries. \begin \sigma_1 = \sigma_\mathrm &= \begin 0&1\\ 1&0 \end \\ \sigma_2 = \sigma_\mathrm &= \begin 0& -i \\ i&0 \end \\ \sigma_3 = \sigma_\mathrm &= \begin 1&0\\ 0&-1 \end \\ \end These matrices are named after the physicist Wolfgang Pauli. In quantum mechanics, they occur in the Pauli equation which takes into account the interaction of the spin of a particle with an external electromagnetic field. They also represent the interaction states of two polarization filters for horizontal/vertical polarization, 45 degree polarization (right/left), and circular polarization (right/left). Each Pauli matrix is Hermitian, and together with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
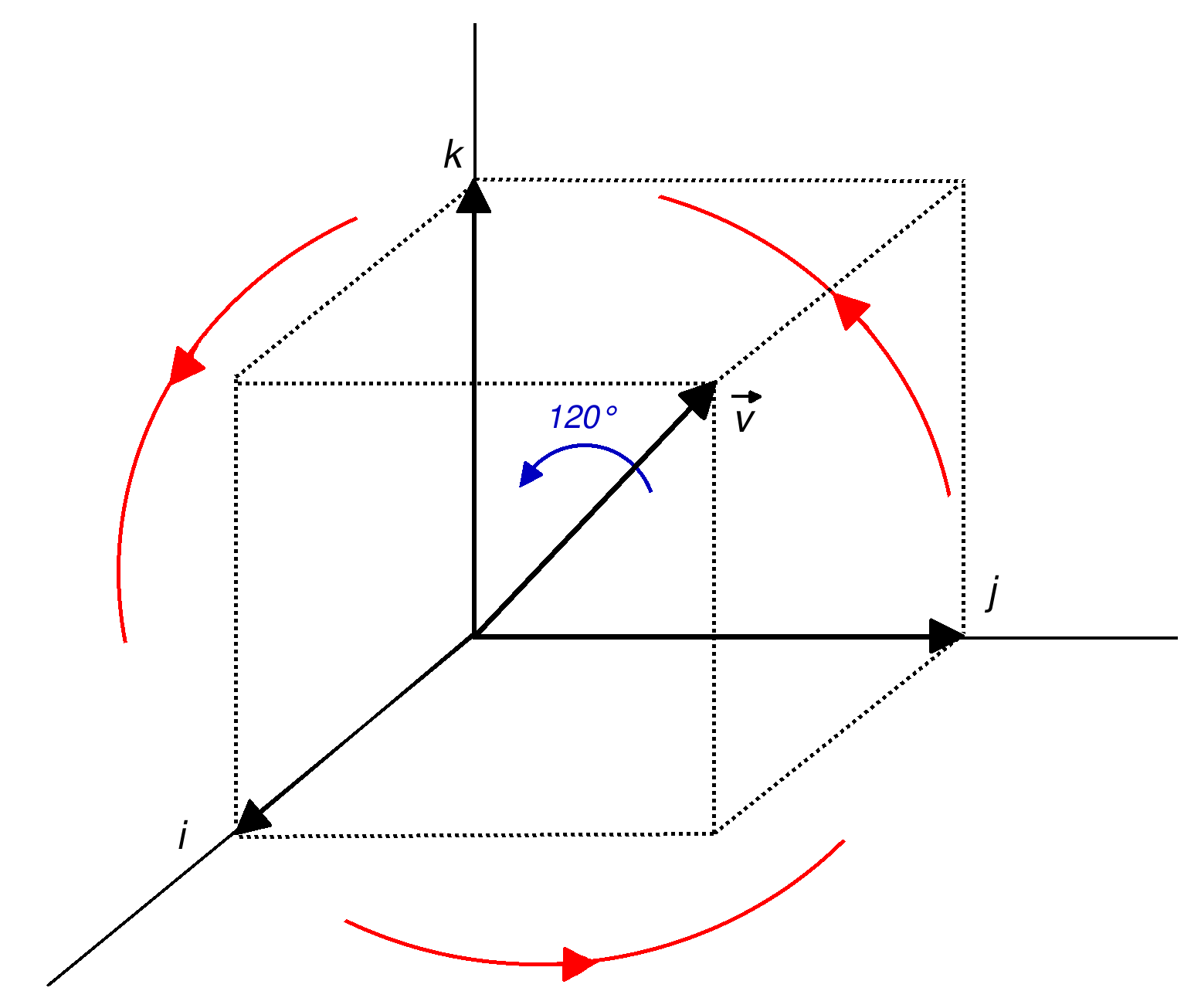
Rotation In Three Dimensions
Rotation, or spin, is the circular movement of an object around a '' central axis''. A two-dimensional rotating object has only one possible central axis and can rotate in either a clockwise or counterclockwise direction. A three-dimensional object has an infinite number of possible central axes and rotational directions. If the rotation axis passes internally through the body's own center of mass, then the body is said to be ''autorotating'' or ''spinning'', and the surface intersection of the axis can be called a '' pole''. A rotation around a completely external axis, e.g. the planet Earth around the Sun, is called ''revolving'' or ''orbiting'', typically when it is produced by gravity, and the ends of the rotation axis can be called the '' orbital poles''. Mathematics Mathematically, a rotation is a rigid body movement which, unlike a translation, keeps a point fixed. This definition applies to rotations within both two and three dimensions (in a plane and in space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3D Rotation Group
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space \R^3 under the operation of composition. By definition, a rotation about the origin is a transformation that preserves the origin, Euclidean distance (so it is an isometry), and orientation (i.e., ''handedness'' of space). Composing two rotations results in another rotation, every rotation has a unique inverse rotation, and the identity map satisfies the definition of a rotation. Owing to the above properties (along composite rotations' associative property), the set of all rotations is a group under composition. Every non-trivial rotation is determined by its axis of rotation (a line through the origin) and its angle of rotation. Rotations are not commutative (for example, rotating ''R'' 90° in the x-y plane followed by ''S'' 90° in the y-z plane is not the same as ''S'' followed by ''R''), making the 3D rotation group a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SO(4)
In mathematics, the group of rotations about a fixed point in four-dimensional Euclidean space is denoted SO(4). The name comes from the fact that it is the special orthogonal group of order 4. In this article ''rotation'' means ''rotational displacement''. For the sake of uniqueness, rotation angles are assumed to be in the segment except where mentioned or clearly implied by the context otherwise. A "fixed plane" is a plane for which every vector in the plane is unchanged after the rotation. An "invariant plane" is a plane for which every vector in the plane, although it may be affected by the rotation, remains in the plane after the rotation. Geometry of 4D rotations Four-dimensional rotations are of two types: simple rotations and double rotations. Simple rotations A simple rotation about a rotation centre leaves an entire plane through (axis-plane) fixed. Every plane that is completely orthogonal to intersects in a certain point . Each such point is the centre of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spinors In Three Dimensions
In mathematics, the spinor concept as specialised to three dimensions can be treated by means of the traditional notions of dot product and cross product. This is part of the detailed algebraic discussion of the rotation group SO(3). Formulation The association of a spinor with a 2×2 complex Hermitian matrix was formulated by Élie Cartan. In detail, given a vector ''x'' = (''x''1, ''x''2, ''x''3) of real (or complex) numbers, one can associate the complex matrix :\vec \rightarrow X \ =\left(\beginx_3&x_1-ix_2\\x_1+ix_2&-x_3\end\right). In physics, this is often written as a dot product X\equiv \cdot , where \equiv (\sigma_1, \sigma_2, \sigma_3) is the vector form of Pauli matrices. Matrices of this form have the following properties, which relate them intrinsically to the geometry of 3-space: * \det X = -, , ^2 , where \det denotes the determinant. * X^2 = , , ^2I , where ''I'' is the identity matrix. * \frac(XY+YX)=(\cdot)I * \frac(XY-YX)=iZ where ''Z'' is the matrix a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Versor
In mathematics, a versor is a quaternion of norm one (a ''unit quaternion''). The word is derived from Latin ''versare'' = "to turn" with the suffix ''-or'' forming a noun from the verb (i.e. ''versor'' = "the turner"). It was introduced by William Rowan Hamilton in the context of his quaternion theory. Each versor has the form :q = \exp(a\mathbf) = \cos a + \mathbf \sin a, \quad \mathbf^2 = -1, \quad a \in ,\pi where the r2 = −1 condition means that r is a unit-length vector quaternion (or that the first component of r is zero, and the last three components of r are a unit vector in 3 dimensions). The corresponding 3-dimensional rotation has the angle 2''a'' about the axis r in axis–angle representation. In case (a right angle), then q = \mathbf, and the resulting unit vector is termed a '' right versor''. Presentation on 3- and 2-spheres Hamilton denoted the versor of a quaternion ''q'' by the symbol U''q''. He was then able to display the general quaternion in polar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quaternions And Spatial Rotation
Unit quaternions, known as ''versors'', provide a convenient mathematical notation for representing spatial orientations and rotations of elements in three dimensional space. Specifically, they encode information about an axis-angle rotation about an arbitrary axis. Rotation and orientation quaternions have applications in computer graphics, Presented at SIGGRAPH '85. computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites, and crystallographic texture analysis. When used to represent rotation, unit quaternions are also called rotation quaternions as they represent the 3D rotation group. When used to represent an orientation (rotation relative to a reference coordinate system), they are called orientation quaternions or attitude quaternions. A spatial rotation around a fixed point of \theta radians about a unit axis (X,Y,Z) that denotes the ''Euler axis'' is given by the quaternion (C, X \, S, Y \, S, Z \, S), where C = \cos(\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation Formalisms In Three Dimensions
In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept is applied to classical mechanics where rotational (or angular) kinematics is the science of quantitative description of a purely rotational motion. The orientation of an object at a given instant is described with the same tools, as it is defined as an imaginary rotation from a reference placement in space, rather than an actually observed rotation from a previous placement in space. According to Euler's rotation theorem the rotation of a rigid body (or three-dimensional coordinate system with the fixed origin) is described by a single rotation about some axis. Such a rotation may be uniquely described by a minimum of three real parameters. However, for various reasons, there are several ways to represent it. Many of these representations use more than the necessary minimum of three parameters, although each of them still has only three degr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of bijective linear transformations of a vector space to itself (i.e. vector space automorphisms); in particular, they can be used to represent group elements as invertible matrices so that the group operation can be represented by matrix multiplication. In chemistry, a group representation can relate mathematical group elements to symmetric rotations and reflections of molecules. Representations of groups are important because they allow many group-theoretic problems to be reduced to problems in linear algebra, which is well understood. They are also important in physics because, for example, they describe how the symmetry group of a physical system affects the solutions of equations describing that system. The term ''representation of a group'' is also used in a more general sense to mean any "description" of a group as a group of transformations of some mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Group
In mathematics, the orthogonal group in dimension , denoted , is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of orthogonal matrices, where the group operation is given by matrix multiplication (an orthogonal matrix is a real matrix whose inverse equals its transpose). The orthogonal group is an algebraic group and a Lie group. It is compact. The orthogonal group in dimension has two connected components. The one that contains the identity element is a normal subgroup, called the special orthogonal group, and denoted . It consists of all orthogonal matrices of determinant . This group is also called the rotation group, generalizing the fact that in dimensions 2 and 3, its elements are the usual ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Group
In mathematics the spin group Spin(''n'') page 15 is the double cover of the special orthogonal group , such that there exists a short exact sequence of Lie groups (when ) :1 \to \mathrm_2 \to \operatorname(n) \to \operatorname(n) \to 1. As a Lie group, Spin(''n'') therefore shares its dimension, , and its Lie algebra with the special orthogonal group. For , Spin(''n'') is simply connected and so coincides with the universal cover of SO(''n''). The non-trivial element of the kernel is denoted −1, which should not be confused with the orthogonal transform of reflection through the origin, generally denoted −. Spin(''n'') can be constructed as a subgroup of the invertible elements in the Clifford algebra Cl(''n''). A distinct article discusses the spin representations. Motivation and physical interpretation The spin group is used in physics to describe the symmetries of (electrically neutral, uncharged) fermions. Its complexification, Spinc, is used to describe elec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |