|
Elias Coding (other)
Elias coding is a term used for one of two types of lossless coding schemes used in digital communications: * Shannon–Fano–Elias coding, a precursor to arithmetic coding, in which probabilities are used to determine codewords * Universal coding using one of Elias' three universal codes, each with predetermined codewords: ** Elias delta coding ** Elias gamma coding Elias \gamma code or Elias gamma code is a universal code encoding positive integers developed by Peter Elias. It is used most commonly when coding integers whose upper bound cannot be determined beforehand. Encoding To code a number ''x''&nb ... ** Elias omega coding {{Disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Digital Communications
Data communication, including data transmission and data reception, is the transfer of data, signal transmission, transmitted and received over a Point-to-point (telecommunications), point-to-point or point-to-multipoint communication channel. Examples of such channels are copper wires, optical fibers, wireless communication using radio spectrum, storage media and computer buses. The data are represented as an electromagnetic signal, such as an electrical voltage, radiowave, microwave, or infrared signal. ''Analog transmission'' is a method of conveying voice, data, image, signal or video information using a continuous signal that varies in amplitude, phase, or some other property in proportion to that of a variable. The messages are either represented by a sequence of pulses by means of a line code (''baseband transmission''), or by a limited set of continuously varying waveforms (''passband transmission''), using a digital modulation method. The passband modulation and cor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
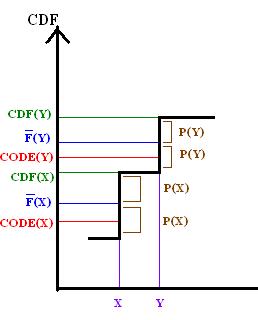
Shannon–Fano–Elias Coding
In information theory, Shannon–Fano–Elias coding is a precursor to arithmetic coding, in which probabilities are used to determine codewords. It is named for Claude Shannon, Robert Fano, and Peter Elias. Algorithm description Given a discrete random variable ''X'' of ordered values to be encoded, let p(x) be the probability for any ''x'' in ''X''. Define a function :\bar F(x) = \sum_p(x_i) + \frac 12 p(x) Algorithm: :For each ''x'' in ''X'', ::Let ''Z'' be the binary expansion of \bar F(x). ::Choose the length of the encoding of ''x'', L(x), to be the integer \left\lceil \log_2 \frac \right\rceil + 1 ::Choose the encoding of ''x'', code(x), be the first L(x) most significant bits after the decimal point of ''Z''. Example Let ''X'' = , with probabilities ''p'' = . :For ''A'' ::\bar F(A) = \frac 12 p(A) = \frac 12 \cdot \frac 13 = 0.1666\ldots ::In binary, ''Z''(''A'') = 0.0010101010... :: L(A) = \left\lceil \log_2 \frac 1 \frac 1 3 \right\rceil + 1 = \mathbf 3 ::co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Arithmetic Coding
Arithmetic coding (AC) is a form of entropy encoding used in lossless data compression. Normally, a String (computer science), string of characters is represented using a fixed number of bits per character, as in the American Standard Code for Information Interchange, ASCII code. When a string is converted to arithmetic encoding, frequently used characters will be stored with fewer bits and not-so-frequently occurring characters will be stored with more bits, resulting in fewer bits used in total. Arithmetic coding differs from other forms of entropy encoding, such as Huffman coding, in that rather than separating the input into component symbols and replacing each with a code, arithmetic coding encodes the entire message into a single number, an arbitrary-precision arithmetic, arbitrary-precision fraction ''q'', where . It represents the current information as a range, defined by two numbers. A recent family of entropy coders called asymmetric numeral systems allows for faster imp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Universal Code (data Compression)
In data compression, a universal code for integers is a prefix code that maps the positive integers onto binary codewords, with the additional property that whatever the true probability distribution on integers, as long as the distribution is monotonic (i.e., ''p''(''i'') ≥ ''p''(''i'' + 1) for all positive ''i''), the expected lengths of the codewords are within a constant factor of the expected lengths that the optimal code for that probability distribution would have assigned. A universal code is ''asymptotically optimal'' if the ratio between actual and optimal expected lengths is bounded by a function of the information entropy of the code that, in addition to being bounded, approaches 1 as entropy approaches infinity. In general, most prefix codes for integers assign longer codewords to larger integers. Such a code can be used to efficiently communicate a message drawn from a set of possible messages, by simply ordering the set of messages ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Elias Delta Coding
Elias δ code or Elias delta code is a universal code encoding the positive integers developed by Peter Elias. Encoding To code a number ''X'' ≥ 1: # Let ''N'' = ⌊log2 ''X''⌋; be the highest power of 2 in ''X'', so 2''N'' ≤ ''X'' < 2''N''+1. # Let ''L'' = ⌊log2 ''N''+1⌋ be the highest power of 2 in ''N''+1, so 2''L'' ≤ ''N''+1 < 2''L''+1. # Write ''L'' zeros, followed by # the ''L''+1-bit binary representation of ''N''+1, followed by # all but the leading bit (i.e. the last ''N'' bits) of ''X''. An equivalent way to express the same process: #Separate ''X'' into the highest power of 2 it contains (2''N'') and the remaining ''N'' binary digits. #Encode ''N''+1 with Elias gamma coding. #Append the remaining ''N'' binary digits to this representation of ''N''+1. To represent a number [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Elias Gamma Coding
Elias \gamma code or Elias gamma code is a universal code encoding positive integers developed by Peter Elias. It is used most commonly when coding integers whose upper bound cannot be determined beforehand. Encoding To code a number ''x'' ≥ 1: # Let N = \lfloor \log_2 x \rfloor be the highest power of 2 it contains, so 2''N'' ≤ ''x'' < 2''N''+1. # Write out N zero bits, then # Append the binary form of x, an (N+1)-bit binary number. An equivalent way to express the same process: # Encode N in unary; that is, as N zeroes followed by a one. # Append the remaining N binary digits of x to this representation of N. To represent a number x, Elias gamma (γ) uses 2 \lfloor \log_2(x) \rfloor + 1 bits. The code begins (the implied probability distribution for the code is added for clarity): Decoding To decode an Elias gamma-coded integer: #Read and count 0s from the stream until you reach the first 1. Call this count of zeroes ''N''. #Considering the one that was r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |