|
Dimensionless Numbers In Fluid Mechanics
Dimensionless numbers in fluid mechanics are a set of dimensionless quantities that have an important role in analyzing the behavior of fluids. Common examples include the Reynolds or the Mach numbers, which describe as ratios the relative magnitude of fluid and physical system characteristics, such as density, viscosity, speed of sound, flow speed, etc. Diffusive numbers in transport phenomena As a general example of how dimensionless numbers arise in fluid mechanics, the classical numbers in transport phenomena of mass, momentum, and energy are principally analyzed by the ratio of effective diffusivities in each transport mechanism. The six dimensionless numbers give the relative strengths of the different phenomena of inertia, viscosity, conductive heat transport, and diffusive mass transport. (In the table, the diagonals give common symbols for the quantities, and the given dimensionless number is the ratio of the left column quantity over top row quantity; e.g. Re = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless Quantity
A dimensionless quantity (also known as a bare quantity, pure quantity, or scalar quantity as well as quantity of dimension one) is a quantity to which no physical dimension is assigned, with a corresponding SI unit of measurement of one (or 1), ISBN 978-92-822-2272-0. which is not explicitly shown. Dimensionless quantities are widely used in many fields, such as mathematics, physics, chemistry, engineering, and economics. Dimensionless quantities are distinct from quantities that have associated dimensions, such as time (measured in seconds). Dimensionless units are dimensionless values that serve as units of measurement for expressing other quantities, such as radians (rad) or steradians (sr) for plane angles and solid angles, respectively. For example, optical extent is defined as having units of metres multiplied by steradians. History Quantities having dimension one, ''dimensionless quantities'', regularly occur in sciences, and are formally treated within the field of d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lewis Number
The Lewis number (Le) is a dimensionless number defined as the ratio of thermal diffusivity to mass diffusivity. It is used to characterize fluid flows where there is simultaneous heat and mass transfer. The Lewis number puts the thickness of the thermal boundary layer in relation to the concentration boundary layer. The Lewis number is defined as :\mathrm = \frac = \frac . where \alpha is the thermal diffusivity and D the mass diffusivity, \lambda the thermal conductivity, \rho the density, D_ the mixture-averaged diffusion coefficient, and c_p the specific heat capacity at constant pressure. In the field of fluid mechanics, many sources define the Lewis number to be the inverse of the above definition. The Lewis number can also be expressed in terms of the Prandtl number and the Schmidt number : :\mathrm = \frac. It is named after Warren K. Lewis (1882–1975), who was the first head of the Chemical Engineering Department at MIT. Some workers in the field of combustion assume (i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Capillary Number
In fluid dynamics, the capillary number (Ca) is a dimensionless quantity representing the relative effect of viscous drag forces versus surface tension forces acting across an interface between a liquid and a gas, or between two immiscible liquids. Alongside the Bond number, commonly denoted Bo, this term is useful to describe the forces acting on a fluid front in porous or granular media, such as soil.Dynamics of viscous entrapped saturated zones in partially wetted porous media Transport in Porous Media (2018), 125(2), 193-210 The capillary number is defined as: : where is the dynamic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ohnesorge Number
The Ohnesorge number (Oh) is a dimensionless number that relates the viscous forces to inertial and surface tension forces. The number was defined by Wolfgang von Ohnesorge in his 1936 doctoral thesis. It is defined as: : \mathrm = \frac = \frac \sim \frac Where * ''μ'' is the dynamic viscosity of the liquid * ''ρ'' is the density of the liquid * ''σ'' is the surface tension * ''L'' is the characteristic length scale (typically drop diameter) * Re is the Reynolds number * We is the Weber number Applications The Ohnesorge number for a 3 mm diameter rain drop is typically ~0.002. Larger Ohnesorge numbers indicate a greater influence of the viscosity. This is often used to relate to free surface fluid dynamics such as dispersion of liquids in gases and in spray technology. English translation: In inkjet printing, liquids whose Ohnesorge number are in the range 0.1 < ''Oh'' < 1.0 are jettable (1 [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity quantifies the internal frictional force between adjacent layers of fluid that are in relative motion. For instance, when a viscous fluid is forced through a tube, it flows more quickly near the tube's axis than near its walls. Experiments show that some stress (such as a pressure difference between the two ends of the tube) is needed to sustain the flow. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion. For a tube with a constant rate of flow, the strength of the compensating force is proportional to the fluid's viscosity. In general, viscosity depends on a fluid's state, such as its temperature, pressure, and rate of deformation. However, the dependence on some of these properties is n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
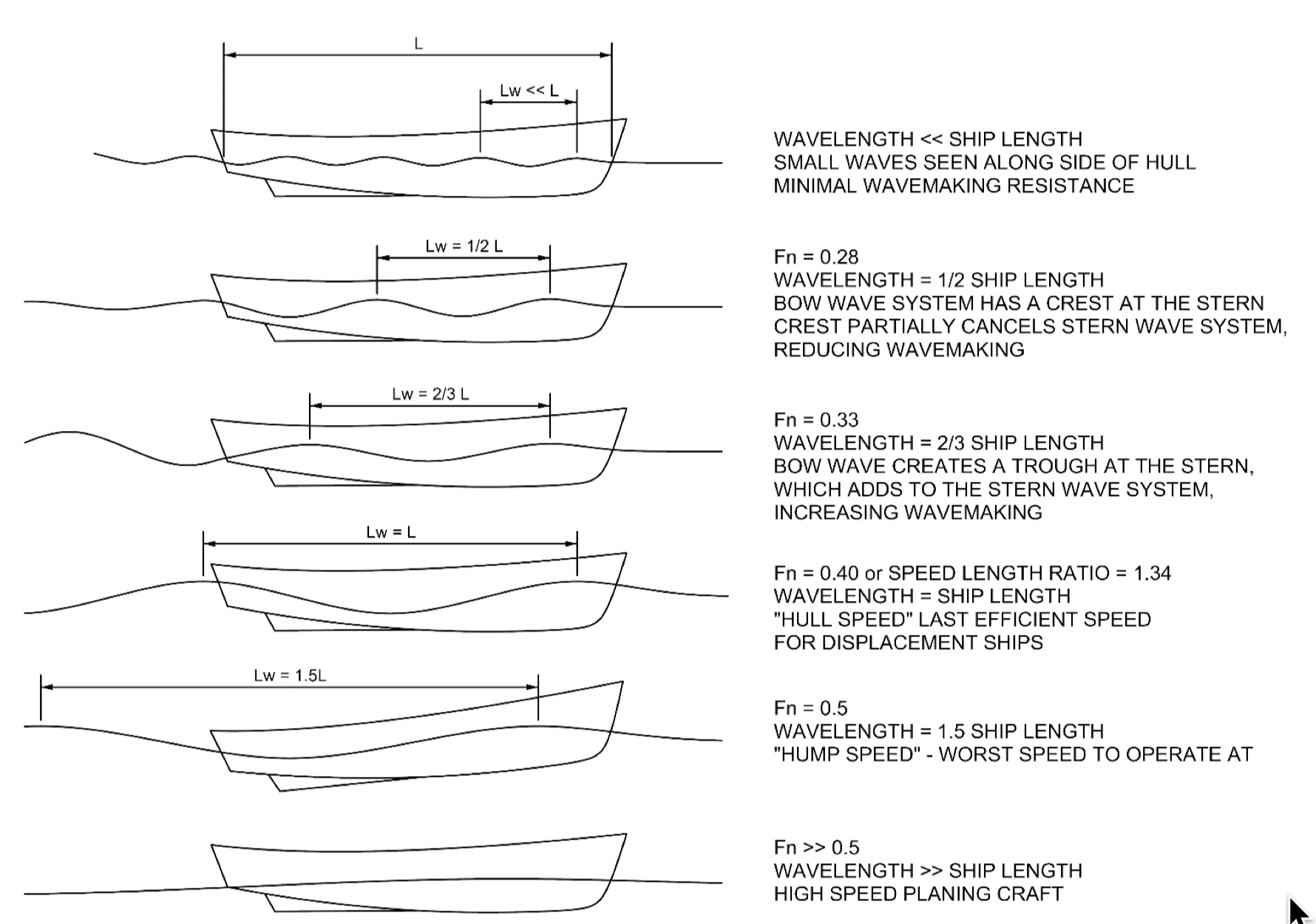
Froude Number
In continuum mechanics, the Froude number (, after William Froude, ) is a dimensionless number defined as the ratio of the flow inertia to the external field (the latter in many applications simply due to gravity). The Froude number is based on the speed–length ratio which he defined as: \mathrm = \frac where is the local flow velocity, is the local external field, and is a characteristic length. The Froude number has some analogy with the Mach number. In theoretical fluid dynamics the Froude number is not frequently considered since usually the equations are considered in the high Froude limit of negligible external field, leading to homogeneous equations that preserve the mathematical aspects. For example, homogeneous Euler equations are conservation equations. However, in naval architecture the Froude number is a significant figure used to determine the resistance of a partially submerged object moving through water. Origins In open channel flows, introduced first th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass Transport
Public transport (also known as public transportation, public transit, mass transit, or simply transit) is a system of transport for passengers by group travel systems available for use by the general public unlike private transport, typically managed on a schedule, operated on established routes, and that charge a posted fee for each trip. There is no rigid definition; the ''Encyclopædia Britannica'' specifies that public transportation is within urban areas, and air travel is often not thought of when discussing public transport—dictionaries use wording like "buses, trains, etc." Examples of public transport include city buses, trolleybuses, trams (or light rail) and passenger trains, rapid transit (metro/subway/underground, etc.) and ferries. Public transport between cities is dominated by airlines, coaches, and intercity rail. High-speed rail networks are being developed in many parts of the world. Most public transport systems run along fixed routes with set embarka ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Conduction
Conduction is the process by which heat is transferred from the hotter end to the colder end of an object. The ability of the object to conduct heat is known as its ''thermal conductivity'', and is denoted . Heat spontaneously flows along a temperature gradient (i.e. from a hotter body to a colder body). For example, heat is conducted from the hotplate of an electric stove to the bottom of a saucepan in contact with it. In the absence of an opposing external driving energy source, within a body or between bodies, temperature differences decay over time, and thermal equilibrium is approached, temperature becoming more uniform. In conduction, the heat flow is within and through the body itself. In contrast, in heat transfer by thermal radiation, the transfer is often between bodies, which may be separated spatially. Heat can also be transferred by a combination of conduction and radiation. In solids, conduction is mediated by the combination of vibrations and collisions of molecu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inertia
Inertia is the idea that an object will continue its current motion until some force causes its speed or direction to change. The term is properly understood as shorthand for "the principle of inertia" as described by Newton in his first law of motion. After some other definitions, Newton states in his first law of motion: The word "perseveres" is a direct translation from Newton's Latin. Other, less forceful terms such as "to continue" or "to remain" are commonly found in modern textbooks. The modern use follows from some changes in Newton's original mechanics (as stated in the ''Principia'') made by Euler, d'Alembert, and other Cartesians. The term inertia comes from the Latin word ''iners'', meaning idle, sluggish. The term inertia may also refer to the resistance of any physical object to a change in its velocity. This includes changes to the object's speed or direction of motion. An aspect of this property is the tendency of objects to keep moving in a straight li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusivity
Diffusivity is a rate of diffusion, a measure of the rate at which particles or heat or fluids can spread. It is measured differently for different mediums. Diffusivity may refer to: *Thermal diffusivity, diffusivity of heat *Diffusivity of mass: ** Mass diffusivity, molecular diffusivity (often called "diffusion coefficient") ** Eddy diffusion, eddy diffusivity * Kinematic viscosity, characterising momentum diffusivity *Magnetic diffusivity Dimensions and Units Diffusivity has dimensions of length2 / time, or m2/s in SI units The International System of Units, known by the international abbreviation SI in all languages and sometimes Pleonasm#Acronyms and initialisms, pleonastically as the SI system, is the modern form of the metric system and the world's most wid ... and cm2/s in CGS units. References Former disambiguation pages converted to set index articles {{SIA ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conservation Of Energy
In physics and chemistry, the law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be ''conserved'' over time. This law, first proposed and tested by Émilie du Châtelet, means that energy can neither be created nor destroyed; rather, it can only be transformed or transferred from one form to another. For instance, chemical energy is converted to kinetic energy when a stick of dynamite explodes. If one adds up all forms of energy that were released in the explosion, such as the kinetic energy and potential energy of the pieces, as well as heat and sound, one will get the exact decrease of chemical energy in the combustion of the dynamite. Classically, conservation of energy was distinct from conservation of mass. However, special relativity shows that mass is related to energy and vice versa by ''E = mc2'', and science now takes the view that mass-energy as a whole is conserved. Theoretically, this implies that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conservation Of Momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass and is its velocity (also a vector quantity), then the object's momentum is : \mathbf = m \mathbf. In the International System of Units (SI), the unit of measurement of momentum is the kilogram metre per second (kg⋅m/s), which is equivalent to the newton-second. Newton's second law of motion states that the rate of change of a body's momentum is equal to the net force acting on it. Momentum depends on the frame of reference, but in any inertial frame it is a ''conserved'' quantity, meaning that if a closed system is not affected by external forces, its total linear momentum does not change. Momentum is also conserved in special relativity (with a modified formula) and, in a modified form, in electrodynamics, quantum mechanics, qu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |