|
Dudley's Entropy Integral
Dudley's entropy integral is a mathematical concept in the field of probability theory that describes a relationship involving the entropy of certain metric spaces and the concentration of measure phenomenon. It is named after the mathematician R. M. Dudley, who introduced the integral as part of his work on the uniform central limit theorem. Definition The Dudley's entropy integral is defined for a metric space (T, d) equipped with a probability measure \mu. Given a set T and an \epsilon-covering, the entropy of T is the logarithm of the minimum number of balls of radius \epsilon required to cover T. Dudley's entropy integral is then given by the formula: \int_0^\infty \sqrt \, d\epsilon where N(T, d, \epsilon) is the covering number, i.e. the minimum number of balls of radius \epsilon with respect to the metric d that cover the space T.Vershynin R. High-Dimensional Probability: An Introduction with Applications in Data Science. Cambridge University Press; 2018. Mathematica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covering Number
In mathematics, a covering number is the number of balls of a given size needed to completely cover a given space, with possible overlaps between the balls. The covering number quantifies the size of a set and can be applied to general metric spaces. Two related concepts are the ''packing number'', the number of disjoint balls that fit in a space, and the ''metric entropy'', the number of points that fit in a space when constrained to lie at some fixed minimum distance apart. Definition Let (''M'', ''d'') be a metric space, let ''K'' be a subset of ''M'', and let ''r'' be a positive real number. Let ''B''''r''(''x'') denote the ball of radius ''r'' centered at ''x''. A subset ''C'' of ''M'' is an ''r-external covering'' of ''K'' if: :K \subseteq \bigcup_ B_r(x). In other words, for every y\in K there exists x\in C such that d(x,y)\leq r. If furthermore ''C'' is a subset of ''K'', then it is an ''r-internal covering''. The external covering number of ''K'', denoted N^_r(K), is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sub-gaussian
In probability theory, a subgaussian distribution, the distribution of a subgaussian random variable, is a probability distribution with strong tail decay. More specifically, the tails of a subgaussian distribution are dominated by (i.e. decay at least as fast as) the tails of a Gaussian. This property gives subgaussian distributions their name. Often in analysis, we divide an object (such as a random variable) into two parts, a central bulk and a distant tail, then analyze each separately. In probability, this division usually goes like "Everything interesting happens near the center. The tail event is so rare, we may safely ignore that." Subgaussian distributions are worthy of study, because the gaussian distribution is well-understood, and so we can give sharp bounds on the rarity of the tail event. Similarly, the subexponential distributions are also worthy of study. Formally, the probability distribution of a random variable ''X '' is called subgaussian if there is a posi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Process
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables in a probability space, where the index of the family often has the interpretation of time. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology Ecology () is the natural science of the relationships among living organisms and their Natural environment, environment. Ecology considers organisms at the individual, population, community (ecology), community, ecosystem, and biosphere lev ..., neuroscience, physics, image processing, signal processing, stochastic control, control theory, information theory, computer scien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
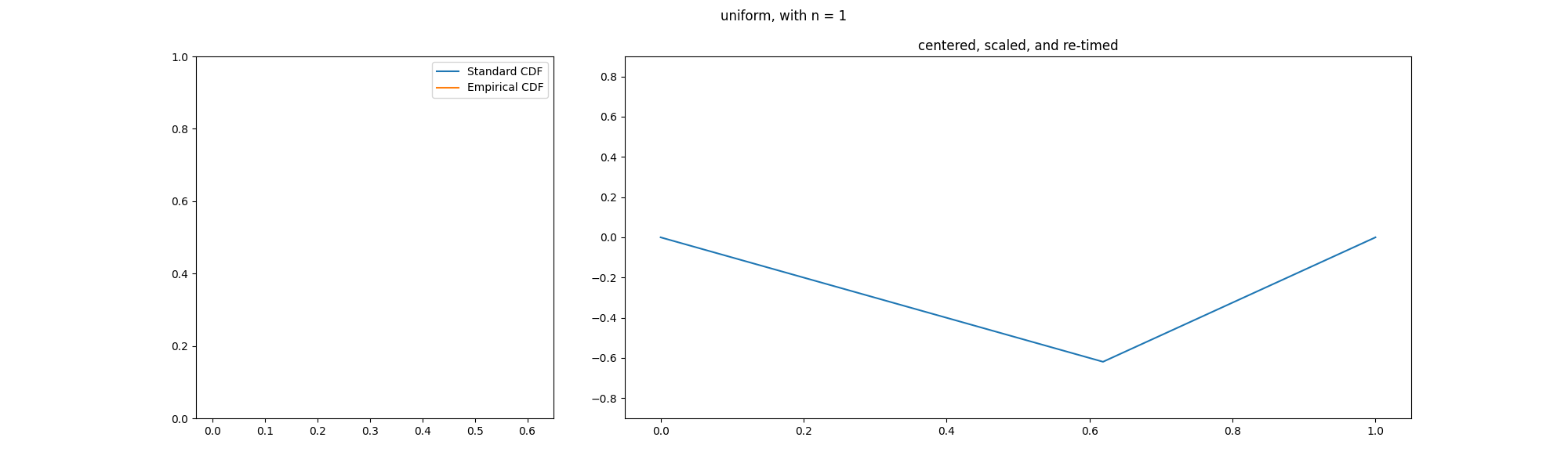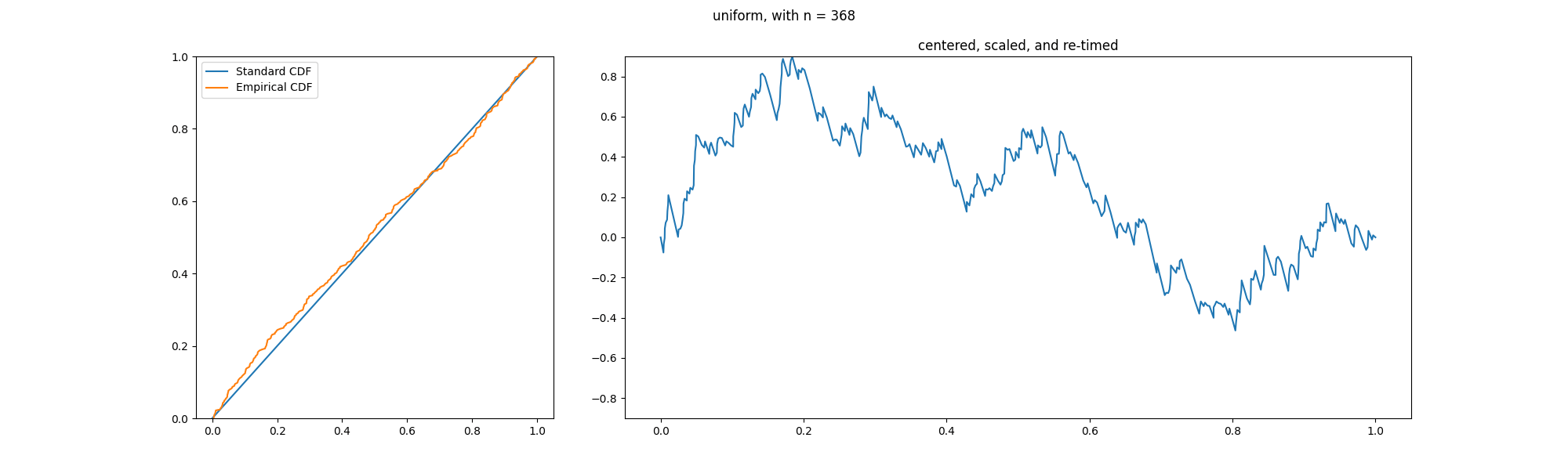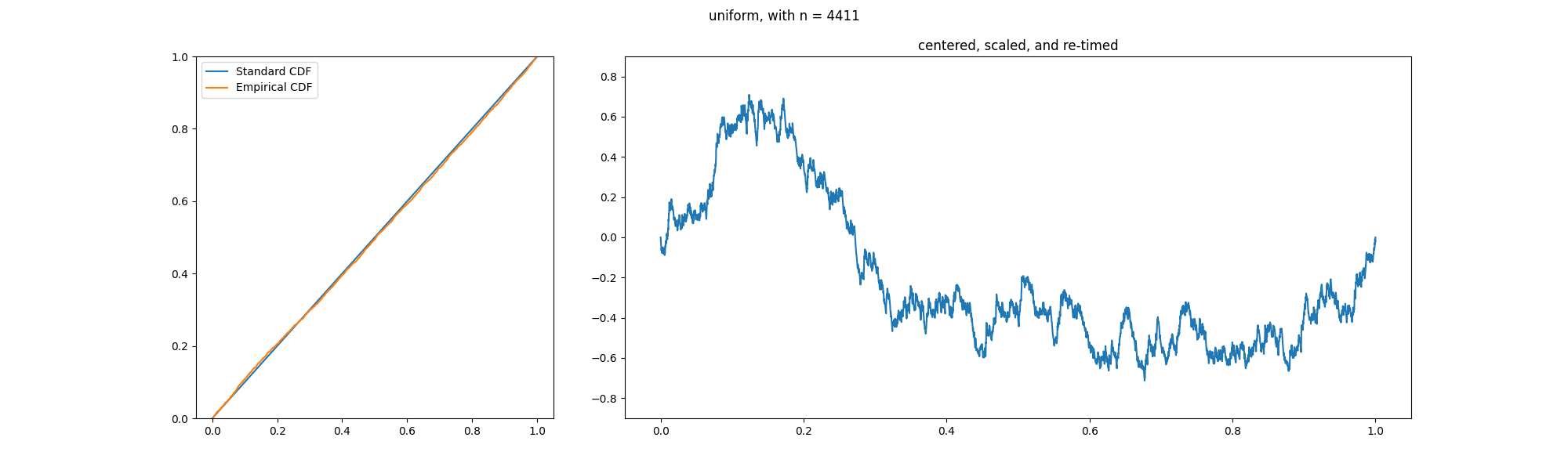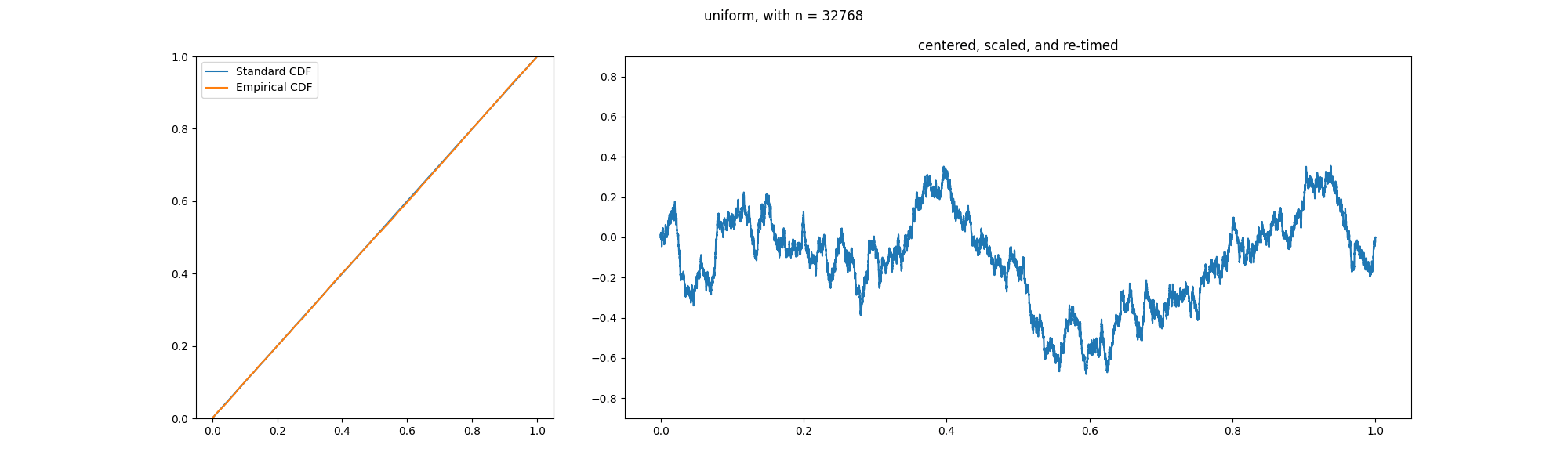
Donsker's Theorem
In probability theory, Donsker's theorem (also known as Donsker's invariance principle, or the functional central limit theorem), named after Monroe D. Donsker, is a functional extension of the central limit theorem for empirical distribution functions. Specifically, the theorem states that an appropriately centered and scaled version of the empirical distribution function converges to a Gaussian process. Let X_1, X_2, X_3, \ldots be a sequence of independent and identically distributed (i.i.d.) random variables with mean 0 and variance 1. Let S_n:=\sum_^n X_i. The stochastic process S:=(S_n)_ is known as a random walk. Define the diffusively rescaled random walk (partial-sum process) by : W^(t) := \frac, \qquad t\in ,1 The central limit theorem asserts that W^(1) converges in distribution to a standard Gaussian random variable W(1) as n\to\infty. Donsker's invariance principle extends this convergence to the whole function W^:=(W^(t))_. More precisely, in its modern form, Do ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy (information Theory)
In information theory, the entropy of a random variable quantifies the average level of uncertainty or information associated with the variable's potential states or possible outcomes. This measures the expected amount of information needed to describe the state of the variable, considering the distribution of probabilities across all potential states. Given a discrete random variable X, which may be any member x within the set \mathcal and is distributed according to p\colon \mathcal\to[0, 1], the entropy is \Eta(X) := -\sum_ p(x) \log p(x), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or "shannon (unit), shannons"), while base Euler's number, ''e'' gives "natural units" nat (unit), nat, and base 10 gives units of "dits", "bans", or "Hartley (unit), hartleys". An equivalent definition of entropy is the expected value of the self-information of a v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covering Number
In mathematics, a covering number is the number of balls of a given size needed to completely cover a given space, with possible overlaps between the balls. The covering number quantifies the size of a set and can be applied to general metric spaces. Two related concepts are the ''packing number'', the number of disjoint balls that fit in a space, and the ''metric entropy'', the number of points that fit in a space when constrained to lie at some fixed minimum distance apart. Definition Let (''M'', ''d'') be a metric space, let ''K'' be a subset of ''M'', and let ''r'' be a positive real number. Let ''B''''r''(''x'') denote the ball of radius ''r'' centered at ''x''. A subset ''C'' of ''M'' is an ''r-external covering'' of ''K'' if: :K \subseteq \bigcup_ B_r(x). In other words, for every y\in K there exists x\in C such that d(x,y)\leq r. If furthermore ''C'' is a subset of ''K'', then it is an ''r-internal covering''. The external covering number of ''K'', denoted N^_r(K), is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Donsker's Theorem
In probability theory, Donsker's theorem (also known as Donsker's invariance principle, or the functional central limit theorem), named after Monroe D. Donsker, is a functional extension of the central limit theorem for empirical distribution functions. Specifically, the theorem states that an appropriately centered and scaled version of the empirical distribution function converges to a Gaussian process. Let X_1, X_2, X_3, \ldots be a sequence of independent and identically distributed (i.i.d.) random variables with mean 0 and variance 1. Let S_n:=\sum_^n X_i. The stochastic process S:=(S_n)_ is known as a random walk. Define the diffusively rescaled random walk (partial-sum process) by : W^(t) := \frac, \qquad t\in ,1 The central limit theorem asserts that W^(1) converges in distribution to a standard Gaussian random variable W(1) as n\to\infty. Donsker's invariance principle extends this convergence to the whole function W^:=(W^(t))_. More precisely, in its modern form, Do ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy And Information
Entropy is a Science, scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, Atmospheric science, weather science, climate change and information systems including the transmission of information in Telecommunications, telecommunication. Entropy is central to the second law of thermodynamics, which states that the entropy of an isolated system left to spontaneous evolution cannot decrease with time. As a result, isolated systems evolve toward thermodynamic equilibrium, where the entropy is highest. A consequence of the second law of thermodynamics is that certain p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |