|
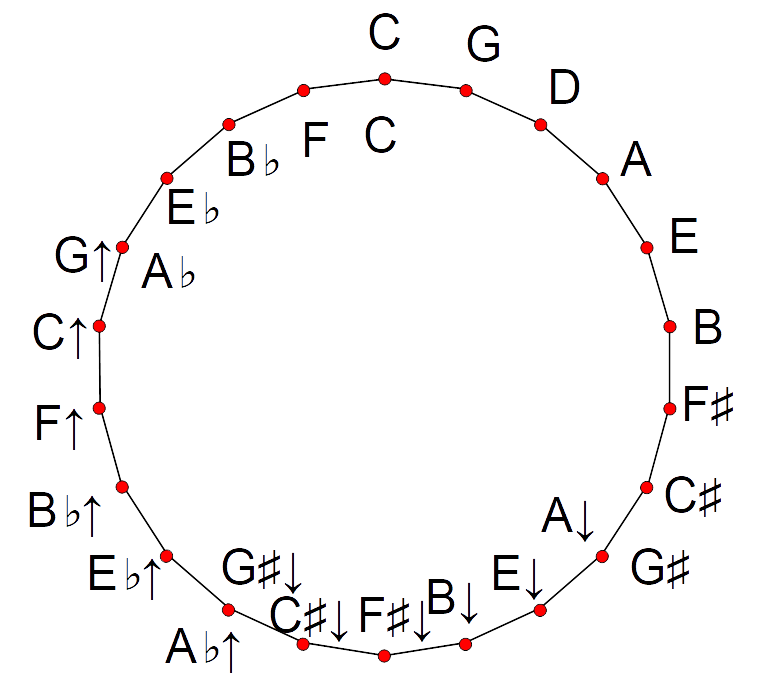
Diminished Third
In classical music from Western culture, a diminished third () is the interval (music), musical interval produced by Diminution, narrowing a minor third by a chromatic semitone.Benward & Saker (2003). ''Music: In Theory and Practice, Vol. I'', p.54. . For instance, the interval from A to C is a minor third, three semitones wide, and both the intervals from A to C, and from A to C are diminished thirds, two semitones wide. Being diminished, it is considered a consonance and dissonance, dissonant interval. In 12-tone equal temperament a diminished third is enharmonic with the major second, both having a value of 200 cent (music), cents. However, in meantone temperament, meantone tunings with fifths flatter than 700 cents, the diminished third is wider than the major second. In 19 equal temperament it is in fact enharmonically equivalent to an augmented second, both having a value of 252.6 cents. In 31 equal temperament it has a more typical value of 232.3 cents. In a twelve-note ke ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augmented Sixth
In music, an augmented sixth () is an Interval (music), interval produced by Augmentation (music), widening a major sixth by a chromatic semitone.Benward & Saker (2003). ''Music: In Theory and Practice, Vol. I'', p.54. . Specific example of an A6 not given but general example of augmenting major intervals described. For instance, the interval from C to A is a major sixth, nine semitones wide, and both the intervals from C to A, and from C to A are augmented sixths, spanning ten semitones. Being augmented, it is considered a consonance and dissonance, dissonant interval. Its Inverted chord, inversion is the diminished third, and its enharmonic equivalent is the minor seventh. In septimal meantone temperament, it is specifically equivalent to the harmonic seventh (a just intonation, just interval of 7:4). In 12-tone equal temperament, the augmented sixth is equal to ten semitones and is a consonance and dissonance, dissonant interval. The augmented sixth is relatively rare. Its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
19 Equal Temperament
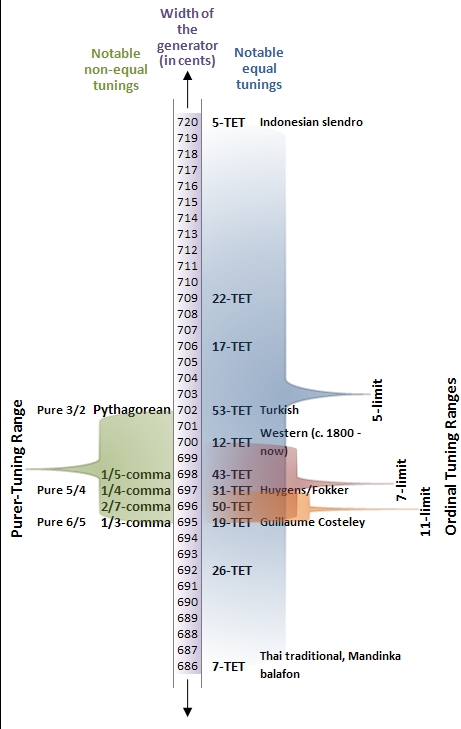
In music, 19 equal temperament, called 19 TET, 19 EDO ("Equal Division of the Octave"), 19-ED2 ("Equal Division of 2:1) or 19 Equal temperament, ET, is the musical temperament, tempered scale derived by dividing the octave into 19 equal steps (equal frequency ratios). Each step represents a frequency ratio of , or 63.16 cent (music), cents (). The fact that traditional western music maps unambiguously onto this scale (unless it presupposes 12-EDO enharmonic equivalences) makes it easier to perform such music in this tuning than in many other tunings. 19 EDO is the tuning of the syntonic temperament in which the tempered perfect fifth is equal to 694.737 cents, as shown in Figure 1 (look for the label "19 TET"). On an isomorphic keyboard, the fingering of music composed in 19 EDO is precisely the same as it is in any other syntonic tuning (such as 12-TET, 12 EDO), so long as the notes are "spelled properly" – that is, with no assumption t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Meantone Intervals
The following is a list of intervals of extended meantone temperament. These intervals constitute the standard vocabulary of intervals for the Western common practice era. Here 12 EDO refers to the size of the interval in the temperament with 12 equal divisions of the octave, which is the most common meantone temperament in the modern era, 19 EDO to 19 equal temperament, 31 EDO to 31 equal temperament, and 50 EDO to 50 equal temperament. Note that for brevity, several of the intervals for 31 EDO and 50 EDO are omitted from the table. R.W. Duffin writes: : "Specifying that the major semitone should be the minor semitone creates a 31 note division of the octave, which, in turn, closely corresponds to extended-quarter-comma meantone ... the 5:4 ratio extended-sixth-comma meantone corresponds to the 55 division ... extended-fifth-comma meantone the 43 division of the octave ratio of the major to minor semitone is 4:3." ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augmented Sixth Chord
In music theory, an augmented sixth chord contains the interval (music), interval of an augmented sixth, usually above its bass note, bass tone. This chord (music), chord has its origins in the Renaissance music, Renaissance, was further developed in the Baroque music, Baroque, and became a distinctive part of the musical style of the Classical period (music), Classical and Romantic period (music), Romantic periods. Conventionally used with a predominant chord, predominant diatonic function, function (resolution (music), resolving to the dominant (music), dominant), the three most common types of augmented sixth chords are usually called the ''Italian sixth'', the ''French sixth'', and the ''German sixth''. Augmented sixth interval The augmented sixth interval is typically between the sixth scale degree, degree of the Major and minor, minor scale, , and the raised fourth degree, . With standard voice leading, the chord is followed directly or indirectly by some form of the do ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Common Practice
In Western classical music, the common practice period (CPP) was the period of about 250 years during which the tonal system was regarded as the only basis for composition. It began when composers' use of the tonal system had clearly superseded earlier systems, and ended when some composers began using significantly modified versions of the tonal system, and began developing other systems as well. Most features of common practice (the accepted concepts of composition during this time) persisted from the mid-Baroque period through the Classical and Romantic periods, roughly from 1650 to 1900. There was much stylistic evolution during these centuries, with patterns and conventions flourishing and then declining, such as the sonata form. The most prominent unifying feature throughout the period is a harmonic language to which music theorists can today apply Roman numeral chord analysis; however, the "common" in common practice does not directly refer to any type of harmony, rathe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complement (music)
In music theory, ''complement'' refers to either traditional interval complementation, or the aggregate complementation of twelve-tone and serialism. In interval complementation a complement is the interval which, when added to the original interval, spans an octave in total. For example, a major 3rd is the complement of a minor 6th. The complement of any interval is also known as its ''inverse'' or ''inversion''. Note that the octave and the unison are each other's complements and that the tritone is its own complement (though the latter is "re-spelt" as either an augmented fourth or a diminished fifth, depending on the context). In the aggregate complementation of twelve-tone music and serialism the complement of one set of notes from the chromatic scale contains all the ''other'' notes of the scale. For example, A-B-C-D-E-F-G is ''complemented'' by B-C-E-F-A. Note that ''musical set theory'' broadens the definition of both senses somewhat. Interval complementation Rule ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quarter-comma Meantone
Quarter-comma meantone, or -comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. In this system the perfect fifth is flattened by one quarter of a syntonic comma with respect to its just intonation used in Pythagorean tuning ( frequency ratio the result is \tfrac \times \left(\tfrac\right)^ = \sqrt \approx 1.49535, or a fifth of 696.578 cents. (The 12th power of that value is 125, whereas 7 octaves is 128, and so falls 41.059 cents short.) This fifth is then iterated to generate the diatonic scale and other notes of the temperament. The purpose is to obtain justly intoned major thirds (with a frequency ratio equal to It was described by Pietro Aron in his ''Toscanello de la Musica'' of 1523, by saying the major thirds should be tuned to be "sonorous and just, as united as possible". Later theorists Gioseffo Zarlino and Francisco de Salinas described the tuning with mathematical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Septimal Major Second
In music, the septimal whole tone, septimal major second, supermajor second, or septimal supermajor second is the interval (music), musical interval exactly or approximately equal to an 8/7 ratio of frequencies.Andrew Horner, Lydia Ayres (2002). ''Cooking with Csound: Woodwind and Brass Recipes'', p.131. . "Super-Major Second". It is about 231 cent (music), cents wide in just intonation.Leta E. Miller, Fredric Lieberman (2006). ''Lou Harrison'', p.72. . quarter tone scale, 24 equal temperament does not match this interval particularly well, its nearest representation being at 250 cents, approximately 19 cents sharp. The 7-limit tuning, septimal whole tone may be derived from the Harmonic series (music), harmonic series as the interval between the seventh harmonic, seventh and eighth harmonics and the term ''septimal'' refers to the fact that it utilizes the Harmonic seventh, seventh harmonic. It can also be thought of as the octave inversion of the 7/4 interval, the harmonic sev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Septimal Meantone Temperament
In music, septimal meantone temperament, also called ''standard septimal meantone'' or simply ''septimal meantone'', refers to the tempering of 7-limit musical intervals by a meantone temperament tuning in the range from fifths flattened by the amount of fifths for 12 equal temperament to those as flat as 19 equal temperament, with 31 equal temperament being a more or less optimal tuning for both the 5- and 7-limits. Choice of temperament Meantone temperament produces a frequency ratio of approximately 5 by means of four fifths, so that the major third (for instance C–E) is obtained from two successive whole tones. Septimal meantone produces the frequency ratio of 56 by ten fifths, so that the interval 7:4 is reached by five successive tones. Hence C–A, not C–B, represents a 7:4 interval in septimal meantone. : There are several slightly adjusted meantone tunings very nearly equivalent to exact quarter comma meantone, which all have good renditions of harmonic seventh i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
22 Equal Temperament
In music, 22 equal temperament, called 22-TET, 22- EDO, or 22-ET, is the tempered scale derived by dividing the octave into 22 equal steps (equal frequency ratios). Each step represents a frequency ratio of , or 54.55 cents (). When composing with 22-ET, one needs to take into account a variety of considerations. Considering the 5-limit, there is a difference between 3 fifths and the sum of 1 fourth and 1 major third. It means that, starting from C, there are two A's—one 16 steps and one 17 steps away. There is also a difference between a major tone and a minor tone. In C major, the second note (D) will be 4 steps away. However, in A minor, where A is 6 steps below C, the fourth note (D) will be 9 steps above A, so 3 steps above C. So when switching from C major to A minor, one needs to slightly change the D note. These discrepancies arise because, unlike 12-ET, 22-ET does not temper out the syntonic comma of 81/80, but instead exaggerates its size by mapping it to one ste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
17 Equal Temperament
In music, 17 equal temperament is the musical temperament, tempered scale (music), scale derived by dividing the octave into 17 equal temperament, equal steps (equal frequency ratios). Each step represents a frequency ratio of , or 70.6 cent (music), cents. 17-ET is the tuning of the regular diatonic tuning in which the tempered perfect fifth is equal to 705.88 cents, as shown in Figure 1 (look for the label "17-TET"). History and use Alexander John Ellis, Alexander J. Ellis refers to a tuning of seventeen tones based on perfect fourths and perfect fifth, fifths as the Arabic scale.Alexander John Ellis, Ellis, Alexander J. (1863). "On the Temperament of Musical Instruments with Fixed Tones", ''Proceedings of the Royal Society of London'', vol. 13. (1863–1864), pp. 404–422. In the thirteenth century, Middle-Eastern musician Safi al-Din Urmawi developed a theoretical system of seventeen tones to describe Arabic and Persian music, although the tones were not equally spaced. This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
31 Equal Temperament
In music, 31 equal temperament, which can also be abbreviated (31 tone ) or (equal division of the octave), also known as tricesimoprimal, is the tempered scale derived by dividing the octave into 31 equally-proportioned steps (equal frequency ratios). Each step represents a frequency ratio of , or 38.71 cents (). is a very good approximation of quarter-comma meantone temperament. More generally, it is a regular diatonic tuning in which the tempered perfect fifth is equal to 696.77 cents, as shown in Figure 1. On an isomorphic keyboard, the fingering of music composed in is precisely the same as it is in any other syntonic tuning (such as so long as the notes are spelled properly—that is, with no assumption of enharmonicity. History and use Division of the octave into 31 steps arose naturally out of Renaissance music theory; the lesser diesis – the ratio of an octave to three major thirds, 128:125 or 41.06 cents – was app ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |