|
Diffusion MRI
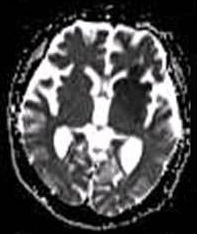
Diffusion-weighted magnetic resonance imaging (DWI or DW-MRI) is the use of specific MRI sequences as well as software that generates images from the resulting data that uses the diffusion of water molecules to generate contrast (vision), contrast in MR images. It allows the mapping of the diffusion process of molecules, mainly water, in biological tissues, in vivo and non-invasively. Molecular diffusion in tissues is not random, but reflects interactions with many obstacles, such as macromolecules, fibers, and Biological membrane, membranes. Water molecule diffusion patterns can therefore reveal microscopic details about tissue architecture, either normal or in a diseased state. A special kind of DWI, diffusion tensor imaging (DTI), has been used extensively to map white matter tractography in the brain. Introduction In diffusion weighted imaging (DWI), the intensity of each image element (voxel) reflects the best estimate of the rate of water diffusion at that location. Because ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
MRI Sequence
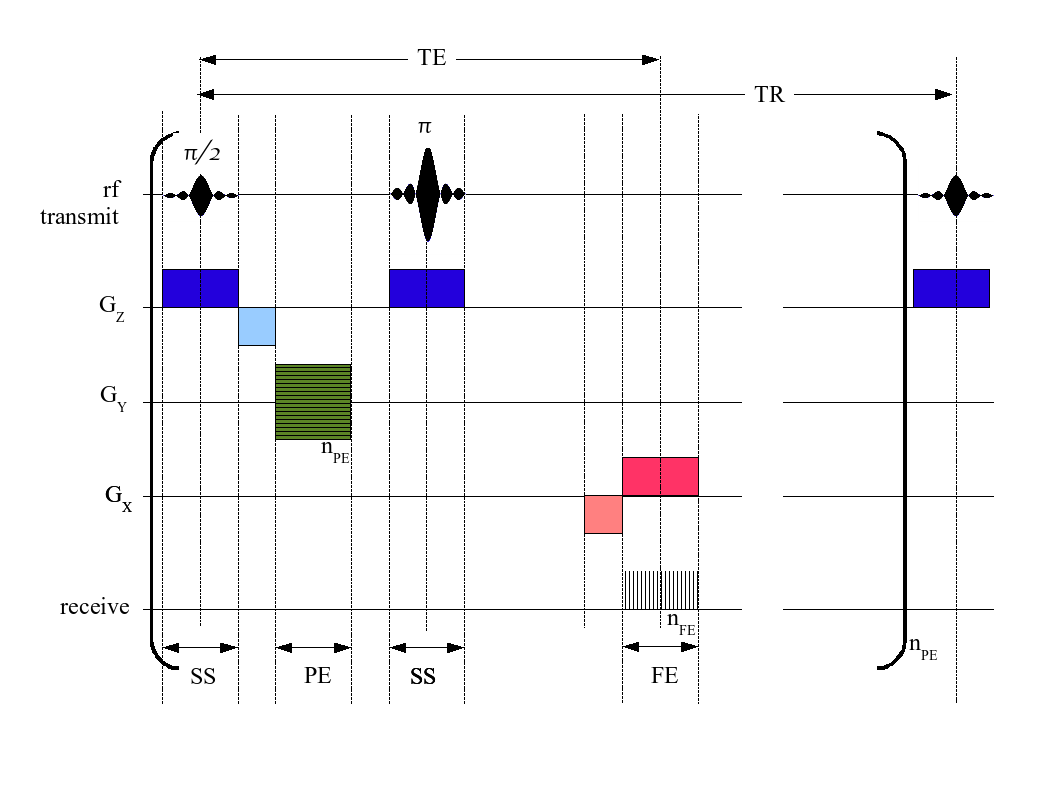
An MRI pulse sequence in magnetic resonance imaging (MRI) is a particular setting of pulse sequences and pulsed field gradients, resulting in a particular image appearance. A multiparametric MRI is a combination of two or more sequences, and/or including Magnetic resonance imaging#Other specialized configurations, other specialized MRI configurations such as In vivo magnetic resonance spectroscopy, spectroscopy. Spin echo T1 and T2 Each tissue returns to its equilibrium state after excitation by the independent relaxation processes of T1 (Spin–lattice relaxation, spin-lattice; that is, magnetization in the same direction as the static magnetic field) and T2 (Spin-spin relaxation time, spin-spin; transverse to the static magnetic field). To create a T1-weighted image, magnetization is allowed to recover before measuring the MR signal by changing the repetition time (TR). This image weighting is useful for assessing the cerebral cortex, identifying fatty tissue, characteriz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Axons
An axon (from Greek ἄξων ''áxōn'', axis) or nerve fiber (or nerve fibre: see spelling differences) is a long, slender projection of a nerve cell, or neuron, in vertebrates, that typically conducts electrical impulses known as action potentials away from the nerve cell body. The function of the axon is to transmit information to different neurons, muscles, and glands. In certain sensory neurons ( pseudounipolar neurons), such as those for touch and warmth, the axons are called afferent nerve fibers and the electrical impulse travels along these from the periphery to the cell body and from the cell body to the spinal cord along another branch of the same axon. Axon dysfunction can be the cause of many inherited and acquired neurological disorders that affect both the peripheral and central neurons. Nerve fibers are classed into three types group A nerve fibers, group B nerve fibers, and group C nerve fibers. Groups A and B are myelinated, and group C are unmyelina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Continuity Equation
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations. Continuity equations are a stronger, local form of conservation laws. For example, a weak version of the law of conservation of energy states that energy can neither be created nor destroyed—i.e., the total amount of energy in the universe is fixed. This statement does not rule out the possibility that a quantity of energy could disappear from one point while simultaneously appearing at another point. A stronger statement is that energy is ''locally'' conserved: energy can neither be created nor destroyed, ''nor'' can it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Diffusion Coefficient
Diffusivity, mass diffusivity or diffusion coefficient is usually written as the proportionality constant between the molar flux due to molecular diffusion and the negative value of the gradient in the concentration of the species. More accurately, the diffusion coefficient times the local concentration is the proportionality constant between the negative value of the mole fraction gradient and the molar flux. This distinction is especially significant in gaseous systems with strong temperature gradients. Diffusivity derives its definition from Fick's law and plays a role in numerous other equations of physical chemistry. The diffusivity is generally prescribed for a given pair of species and pairwise for a multi-species system. The higher the diffusivity (of one substance with respect to another), the faster they diffuse into each other. Typically, a compound's diffusion coefficient is ~10,000× as great in air as in water. Carbon dioxide in air has a diffusion coefficient of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of f. If the gradient of a function is non-zero at a point p, the direction of the gradient is the direction in which the function increases most quickly from p, and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function f(\mathbf) may be defined by: df=\nabla f \cdot d\mathbf where df is the total infinitesimal change in f for a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fick's Laws Of Diffusion
Fick's laws of diffusion describe diffusion and were first posited by Adolf Fick in 1855 on the basis of largely experimental results. They can be used to solve for the diffusion coefficient, . Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation. ''Fick's first law'': Movement of particles from high to low concentration (diffusive flux) is directly proportional to the particle's concentration gradient. ''Fick's second law'': Prediction of change in concentration gradient with time due to diffusion. A diffusion process that obeys Fick's laws is called normal or Fickian diffusion; otherwise, it is called anomalous diffusion or non-Fickian diffusion. History In 1855, physiologist Adolf Fick first reported* * his now well-known laws governing the transport of mass through diffusive means. Fick's work was inspired by the earlier experiments of Thomas Graham, which fell short of proposing the fundamental laws for which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gyromagnetic Ratio
In physics, the gyromagnetic ratio (also sometimes known as the magnetogyric ratio in other disciplines) of a particle or system is the ratio of its magnetic moment to its angular momentum, and it is often denoted by the symbol , gamma. Its SI unit is the reciprocal second per tesla (s−1⋅T−1) or, equivalently, the coulomb per kilogram (C⋅kg−1). The -factor of a particle is a related dimensionless value of the system, derived as the ratio of its gyromagnetic ratio to that which would be classically expected from a rigid body of which the mass and charge are distributed identically, and for which total mass and charge are the same as that of the system. For a classical rotating body Consider a nonconductive charged body rotating about an axis of symmetry. According to the laws of classical physics, it has both a magnetic dipole moment due to the movement of charge and an angular momentum due to the movement of mass arising from its rotation. It can be shown that as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Moiety (chemistry)
In organic chemistry, a moiety ( ) is a part of a molecule that is given a name because it is identified as a part of other molecules as well. Typically, the term is used to describe the larger and characteristic parts of organic molecules, and it should not be used to describe or name smaller functional groups of atoms that chemically react in similar ways in most molecules that contain them. Occasionally, a moiety may contain smaller moieties and functional groups. A moiety that acts as a branch extending from the backbone of a hydrocarbon molecule is called a substituent or side chain, which typically can be removed from the molecule and substituted with others. The term is also used in pharmacology, where an active moiety is the part of a molecule responsible for the physiological or pharmacological action of a drug. Active moiety In pharmacology, an active moiety is the part of a molecule or ion—excluding appended inactive portions—that is responsible for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
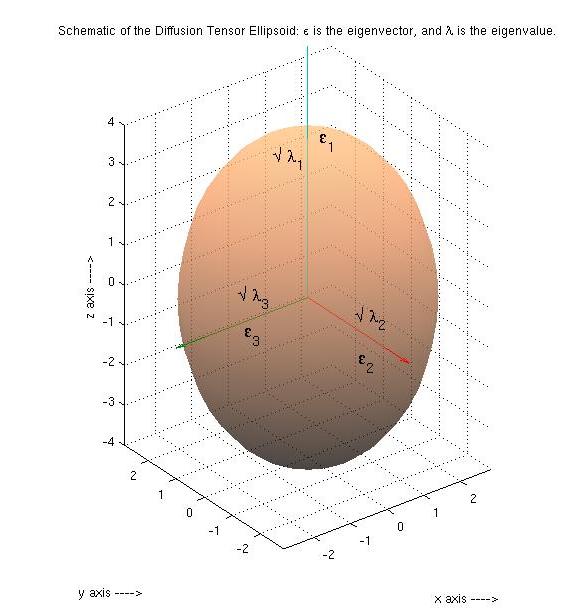
Fractional Anisotropy
Fractional anisotropy (FA) is a scalar (mathematics), scalar value between zero and one that describes the degree of anisotropy of a diffusion process. A value of zero means that diffusion is isotropic, i.e. it is unrestricted (or equally restricted) in all directions. A value of one means that diffusion occurs only along one axis and is fully restricted along all other directions. FA is a measure often used in diffusion imaging where it is thought to reflect fiber density, axonal diameter, and myelination in white matter. The FA is an extension of the concept of Eccentricity (mathematics), eccentricity of conic sections in 3 dimensions, normalized to the unit range. Definition A Diffusion Ellipsoid is completely represented by the Diffusion Tensor, D. FA is calculated from the eigenvalues \lambda_1 \ge \lambda_2 \ge \lambda_3 of the diffusion tensor. The eigenvectors give the directions in which the ellipsoid has major axes, and the corresponding eigenvalues give the magnitude of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors (which are the simplest tensors), dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system; those components form an array, which can be thought of as a high-dimensional matrix. Tensors have become important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as mechanics ( stress, elasticity, quantum mechanics, fluid mechanics, moment of inertia, ...), electrodynamics ( electromagnetic ten ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Stroke
Stroke is a medical condition in which poor cerebral circulation, blood flow to a part of the brain causes cell death. There are two main types of stroke: brain ischemia, ischemic, due to lack of blood flow, and intracranial hemorrhage, hemorrhagic, due to bleeding. Both cause parts of the brain to stop functioning properly. Signs and symptoms of stroke may include an hemiplegia, inability to move or feel on one side of the body, receptive aphasia, problems understanding or expressive aphasia, speaking, dizziness, or homonymous hemianopsia, loss of vision to one side. Signs and symptoms often appear soon after the stroke has occurred. If symptoms last less than 24 hours, the stroke is a transient ischemic attack (TIA), also called a mini-stroke. subarachnoid hemorrhage, Hemorrhagic stroke may also be associated with a thunderclap headache, severe headache. The symptoms of stroke can be permanent. Long-term complications may include pneumonia and Urinary incontinence, loss of b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Edema
Edema (American English), also spelled oedema (British English), and also known as fluid retention, swelling, dropsy and hydropsy, is the build-up of fluid in the body's tissue (biology), tissue. Most commonly, the legs or arms are affected. Symptoms may include skin that feels tight, the area feeling heavy, and joint stiffness. Other symptoms depend on the underlying cause. Causes may include Chronic venous insufficiency, venous insufficiency, heart failure, kidney problems, hypoalbuminemia, low protein levels, liver problems, deep vein thrombosis, infections, kwashiorkor, angioedema, certain medications, and lymphedema. It may also occur in immobile patients (stroke, spinal cord injury, aging), or with temporary immobility such as prolonged sitting or standing, and during menstruation or pregnancy. The condition is more concerning if it starts suddenly, or pain or shortness of breath is present. Treatment depends on the underlying cause. If the underlying mechanism involve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |