|
Degree Of Coherence
In quantum optics, correlation functions are used to characterize the statistical and Coherence (physics), coherence properties – the ability of waves to interfere – of electromagnetic radiation, like optical light. Higher order coherence or ''n''-th order coherence (for any positive integer ''n''>1) extends the concept of coherence to quantum optics and coincidence experiments. It is used to differentiate between optics experiments that require a Quantum electrodynamics, quantum mechanical description from those for which classical fields suffice. Classical optical experiments like Young's interference experiment, Young's double slit experiment and Mach–Zehnder interferometer, Mach-Zehnder interferometry are characterized only by the first order coherence. The 1956 Hanbury Brown and Twiss effect, Hanbury Brown and Twiss experiment brought to light a different kind of correlation between fields, namely the correlation of intensities, which correspond to second order coheren ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Optics
Quantum optics is a branch of atomic, molecular, and optical physics and quantum chemistry that studies the behavior of photons (individual quanta of light). It includes the study of the particle-like properties of photons and their interaction with, for instance, atoms and molecules. Photons have been used to test many of the counter-intuitive predictions of quantum mechanics, such as entanglement and teleportation, and are a useful resource for quantum information processing. History Light propagating in a restricted volume of space has its energy and momentum quantized according to an integer number of particles known as photons. Quantum optics studies the nature and effects of light as quantized photons. The first major development leading to that understanding was the correct modeling of the blackbody radiation spectrum by Max Planck in 1899 under the hypothesis of light being emitted in discrete units of energy. The photoelectric effect was further evidence of thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interferometric Visibility
The interferometric visibility (also known as interference visibility and fringe visibility, or just visibility when in context) is a measure of the contrast of ''interference'' in any system subject to wave superposition. Examples include as optics, quantum mechanics, water waves, sound waves, or electrical signals. Visibility is defined as the ratio of the amplitude of the interference pattern to the sum of the powers of the individual waves. The interferometric visibility gives a practical way to measure the coherence of two waves (or one wave with itself). A theoretical definition of the coherence is given by the degree of coherence, using the notion of correlation. Generally, two or more waves are superimposed and as the phase difference between them varies, the power or intensity (probability or population in quantum mechanics) of the resulting wave oscillates, forming an interference pattern. The pointwise definition may be expanded to a visibility function varying over ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Correlation
In quantum mechanics, quantum correlation is the expected value of the product of the alternative outcomes. In other words, it is the expected change in physical characteristics as one quantum system passes through an interaction site. In John Bell's 1964 paper that inspired the Bell test, it was assumed that the outcomes A and B could each only take one of two values, -1 or +1. It followed that the product, too, could only be -1 or +1, so that the average value of the product would be :\frac where, for example, N++ is the number of simultaneous instances ("coincidences") of the outcome +1 on both sides of the experiment. However, in actual experiments, detectors are not perfect and produce many null outcomes. The correlation can still be estimated using the sum of coincidences, since clearly zeros do not contribute to the average, but in practice, instead of dividing by Ntotal, it is customary to divide by :N_ + N_+ N_ + N_ the total number of observed coincidences. The leg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
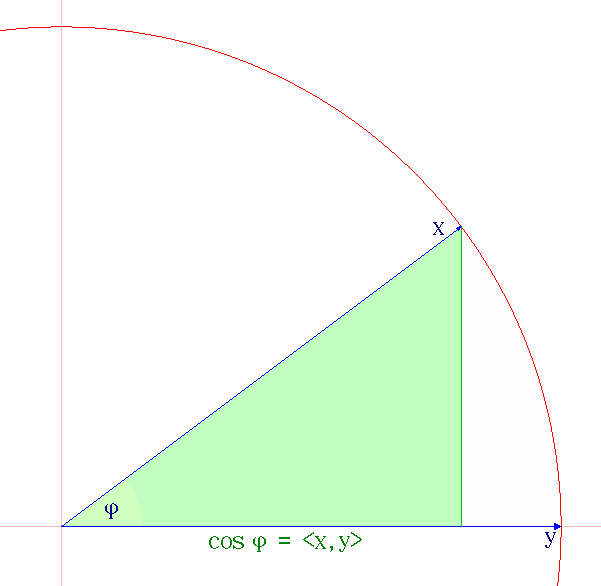
Unit Vector
In mathematics, a unit vector in a normed vector space is a Vector (mathematics and physics), vector (often a vector (geometry), spatial vector) of Norm (mathematics), length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in \hat (pronounced "v-hat"). The term ''normalized vector'' is sometimes used as a synonym for ''unit vector''. The normalized vector û of a non-zero vector u is the unit vector in the direction of u, i.e., :\mathbf = \frac=(\frac, \frac, ... , \frac) where ‖u‖ is the Norm (mathematics), norm (or length) of u and \, \mathbf\, = (u_1, u_2, ..., u_n). The proof is the following: \, \mathbf\, =\sqrt=\sqrt=\sqrt=1 A unit vector is often used to represent direction (geometry), directions, such as normal directions. Unit vectors are often chosen to form the basis (linear algebra), basis of a vector space, and every vector in the space may be written as a linear combination form of unit vectors. Orthogonal coordinates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Vector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength), and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation. A closely related vector is the angular wave vector (or angular wavevector), with a typical unit being radian per metre. The wave vector and angular wave vector are related by a fixed constant of proportionality, 2 radians per cycle. It is common in several fields of physics to refer to the angular wave vector simply as the ''wave vector'', in contrast to, for example, crystallography. It is also common to use the symbol for whichever is in use. In the context of special relativity, a '' wave four-vector'' can be defined, combining the (angular) wave vector and (angular) frequency. Definition The terms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heisenberg Picture
In physics, the Heisenberg picture or Heisenberg representation is a Dynamical pictures, formulation (largely due to Werner Heisenberg in 1925) of quantum mechanics in which observables incorporate a dependency on time, but the quantum state, states are time-independent. It stands in contrast to the Schrödinger picture in which observables are constant and the states evolve in time. It further serves to define a third, hybrid, picture, the interaction picture. Mathematical details In the Heisenberg picture of quantum mechanics the state vectors do not change with time, while observables satisfy where "H" and "S" label observables in Heisenberg and Schrödinger picture respectively, is the Hamiltonian (quantum mechanics), Hamiltonian and denotes the commutator of two operators (in this case and ). Taking expectation values automatically yields the Ehrenfest theorem, featured in the correspondence principle. By the Stone–von Neumann theorem, the Heisenberg picture and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operator (physics)
An operator is a function over a space of physical states onto another space of states. The simplest example of the utility of operators is the study of symmetry (which makes the concept of a group useful in this context). Because of this, they are useful tools in classical mechanics. Operators are even more important in quantum mechanics, where they form an intrinsic part of the formulation of the theory. They play a central role in describing observables (measurable quantities like energy, momentum, etc.). Operators in classical mechanics In classical mechanics, the movement of a particle (or system of particles) is completely determined by the Lagrangian L(q, \dot, t) or equivalently the Hamiltonian H(q, p, t), a function of the generalized coordinates ''q'', generalized velocities \dot = \mathrm q / \mathrm t and its conjugate momenta: :p = \frac If either ''L'' or ''H'' is independent of a generalized coordinate ''q'', meaning the ''L'' and ''H'' do not change when ''q' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Photon Antibunching
Photon antibunching generally refers to a light field with photons more equally spaced than a coherent laser field, a signature being a measured two-time correlation suppressed below that of a coherent laser field. More specifically, it can refer to sub-Poissonian photon statistics, that is a photon number distribution for which the variance is less than the mean. A coherent state, as output by a laser far above threshold, has Poissonian statistics yielding random photon spacing; while a thermal light field has super-Poissonian statistics and yields bunched photon spacing. In the thermal (bunched) case, the number of fluctuations is larger than a coherent state; for an antibunched source they are smaller. Explanation The variance of the photon number distribution is : V_n=\langle \Delta n^2\rangle=\langle n^2\rangle-\langle n\rangle^2= \left\langle \left(a^a\right)^2\right\rangle-\langle a^a\rangle ^2. Using commutation relations, this can be written as : V_n=\langle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Siegert Relation
Siegert () is a German surname derived from the given name Sieghart. Notable people with the name include: * Andrew Siegert (born 1982), Australian footballer * Benjamin Siegert (born 1981), German footballer * Bernhard Siegert Bernhard Siegert (born 1959) is a German media theorist and media historian. Siegert was born in Bremen. He graduated in 1987 in Germanic Studies, Philosophy and History at the Albert-Ludwigs-Universität Freiburg/Germany. He followed Friedrich K ... (born 1959), German media theorist and media historian * Daniel Siegert (born 1991), German singer * Ferdinand Siegert (1865–1946), German paediatrician * Hans Siegert (1914–1966), East German footballer and manager * Herb Siegert (1924–2008), American footballer * Herbert Siegert (1920–2008), German football manager * Larry Siegert (1923–2007), Royal New Zealand Air Force officer * Martin Siegert, British geographer * Tobias Siegert (born 1991), German Grand Prix motorcycle racer See als ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is an upper bound on the absolute value of the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered one of the most important and widely used inequalities in mathematics. Inner products of vectors can describe finite sums (via finite-dimensional vector spaces), infinite series (via vectors in sequence spaces), and integrals (via vectors in Hilbert spaces). The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coherence G2
Coherence is, in general, a state or situation in which all the parts or ideas fit together well so that they form a united whole. More specifically, coherence, coherency, or coherent may refer to the following: Physics * Coherence (physics), an ideal property of waves that enables stationary (i.e. temporally and spatially constant) interference * Coherence (units of measurement), a derived unit that, for a given system of quantities and for a chosen set of base units, is a product of powers of base units with no other proportionality factor than one * Coherence time, the time over which a propagating wave (especially a laser or maser beam) may be considered coherent; the time interval within which its phase is, on average, predictable Mathematics * Coherence (philosophical gambling strategy), a concept in Bayesian statistics * Coherence (signal processing), a statistic that can be used to examine the relation between two signals or data sets * Coherence (statistics), a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |