|
Darken's Equations
In metallurgy, the Darken equations are used to describe the solid-state diffusion of materials in binary solutions. They were first described by Lawrence Stamper Darken in 1948.Darken, L. S. "Diffusion, mobility and their interrelation through free energy in binary metallic systems". Trans. AIME 175.1 (1948): 184–194. The equations apply to cases where a solid solution's two components do not have the same coefficient of diffusion. The equations Darken's first equation is: : \nu = (D_1 - D_2) \frac = (D_2 - D_1) \frac. where: * \nu is the ''marker velocity'' of inert markers showing the diffusive flux. * D_1 and D_2 are the diffusion coefficients of the two components. * N_1 and N_2 are the atomic fractions of the two components. * x represents the direction in which the diffusion is measured. It is important to note that this equation only holds in situations where the total concentration remains constant. Darken's second equation is: :\tilde = (N_1 D_2 + N_2 D_1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metallurgy
Metallurgy is a domain of materials science and engineering that studies the physical and chemical behavior of metallic elements, their inter-metallic compounds, and their mixtures, which are known as alloys. Metallurgy encompasses both the science and the technology of metals, including the production of metals and the engineering of metal components used in products for both consumers and manufacturers. Metallurgy is distinct from the craft of metalworking. Metalworking relies on metallurgy in a similar manner to how medicine relies on medical science for technical advancement. A specialist practitioner of metallurgy is known as a metallurgist. The science of metallurgy is further subdivided into two broad categories: chemical metallurgy and physical metallurgy. Chemical metallurgy is chiefly concerned with the reduction and oxidation of metals, and the chemical performance of metals. Subjects of study in chemical metallurgy include mineral processing, the extraction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Galilean Transformation
In physics, a Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. These transformations together with spatial rotations and translations in space and time form the inhomogeneous Galilean group (assumed throughout below). Without the translations in space and time the group is the homogeneous Galilean group. The Galilean group is the group of motions of Galilean relativity acting on the four dimensions of space and time, forming the Galilean geometry. This is the passive transformation point of view. In special relativity the homogeneous and inhomogeneous Galilean transformations are, respectively, replaced by the Lorentz transformations and Poincaré transformations; conversely, the group contraction in the classical limit of Poincaré transformations yields Galilean transformations. The equations below are only physically valid in a Newtonian fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Bonding
Diffusion bonding or diffusion welding is a solid-state welding technique used in metalworking, capable of joining similar and dissimilar metals. It operates on the principle of solid-state diffusion, wherein the atoms of two solid, metallic surfaces intersperse themselves over time. This is typically accomplished at an elevated temperature, approximately 50-75% of the absolute melting temperature of the materials. A weak bond can also be achieved at room temperature. Diffusion bonding is usually implemented by applying high pressure, in conjunction with necessarily high temperature, to the materials to be welded; the technique is most commonly used to weld "sandwiches" of alternating layers of thin metal foil, and metal wires or filaments. Currently, the diffusion bonding method is widely used in the joining of high-strength and refractory metals within the aerospace and nuclear industries. History The act of diffusion welding is centuries old. This can be found in the form of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
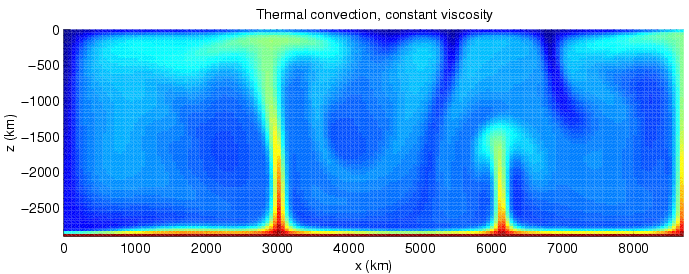
Convection
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow. Convective flow may be Transient state, transient (such as when a Multiphasic liquid, multiphase mixture of oil and water separates) or steady state (see convection cell). The convection may be due to Gravity, gravitational, Electromagnetism, electromagnetic or Fictitious force, fictitious body forces. Convection (heat transfer), Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its Earth's mantle, mantle. Discrete convective cells in the atmosphere can be identified by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gas Constant
The molar gas constant (also known as the gas constant, universal gas constant, or ideal gas constant) is denoted by the symbol or . It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per amount of substance, rather than energy per temperature increment per ''particle''. The constant is also a combination of the constants from Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. It is a physical constant that is featured in many fundamental equations in the physical sciences, such as the ideal gas law, the Arrhenius equation, and the Nernst equation. The gas constant is the constant of proportionality that relates the energy scale in physics to the temperature scale and the scale used for amount of substance. Thus, the value of the gas constant ultimately derives from historical decisions and accidents in the setting of units of energy, temperature and amount of substance. The Boltzmann constant a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Activity (chemistry)
In thermodynamics, activity (symbol ) is a measure of the "effective concentration" of a species in a mixture, in the sense that the species' chemical potential depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution. The term "activity" in this sense was coined by the American chemist Gilbert N. Lewis in 1907. By convention, activity is treated as a dimensionless quantity, although its value depends on customary choices of standard state for the species. The activity of pure substances in condensed phases (solids and liquids) is taken as = 1. Activity depends on temperature, pressure and composition of the mixture, among other things. For gases, the activity is the effective partial pressure, and is usually referred to as fugacity. The difference between activity and other measures of concentration arises because the interactions between different types of molecules in non-ideal gases or solutions are differen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Avogadro Constant
The Avogadro constant, commonly denoted or , is an SI defining constant with an exact value of when expressed in reciprocal moles. It defines the ratio of the number of constituent particles to the amount of substance in a sample, where the particles in question are any designated elementary entity, such as molecules, atoms, ions, ion pairs. The numerical value of this constant is known as the Avogadro number, commonly denoted . The Avogadro ''number'' is an exact number equal to the number of constituent particles in one mole of any substance (by definition of the mole), historically derived from the experimental determination of the number of atoms in 12 grams of carbon-12 (12C) before the 2019 revision of the SI. Both the constant and the number are named after the Italian physicist and chemist Amedeo Avogadro. The Avogadro constant is used as a proportionality factor in relating the ''amount of substance'' , in a sample of a substance , to the corresponding n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flux
Flux describes any effect that appears to pass or travel (whether it actually moves or not) through a surface or substance. Flux is a concept in applied mathematics and vector calculus which has many applications in physics. For transport phenomena, flux is a vector quantity, describing the magnitude and direction of the flow of a substance or property. In vector calculus flux is a scalar quantity, defined as the surface integral of the perpendicular component of a vector field over a surface. Terminology The word ''flux'' comes from Latin: ''fluxus'' means "flow", and ''fluere'' is "to flow". As '' fluxion'', this term was introduced into differential calculus by Isaac Newton. The concept of heat flux was a key contribution of Joseph Fourier, in the analysis of heat transfer phenomena. His seminal treatise ''Théorie analytique de la chaleur'' (''The Analytical Theory of Heat''), defines ''fluxion'' as a central quantity and proceeds to derive the now well-known expre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs–Duhem Equation
In thermodynamics, the Gibbs–Duhem equation describes the relationship between changes in chemical potential for components in a thermodynamic system: \sum_^I N_i \mathrm\mu_i = - S \mathrmT + V \mathrmp where N_i is the number of moles of component i, \mathrm\mu_i the infinitesimal increase in chemical potential for this component, S the entropy, T the absolute temperature, V volume and p the pressure. I is the number of different components in the system. This equation shows that in thermodynamics intensive properties are not independent but related, making it a mathematical statement of the state postulate. When pressure and temperature are variable, only I-1 of I components have independent values for chemical potential and Gibbs' phase rule follows. The Gibbs−Duhem equation applies to homogeneous thermodynamic systems. It does not apply to inhomogeneous systems such as small thermodynamic systems, systems subject to long-range forces like electricity and gravity, or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fick's Laws Of Diffusion
Fick's laws of diffusion describe diffusion and were first posited by Adolf Fick in 1855 on the basis of largely experimental results. They can be used to solve for the diffusion coefficient, . Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation. ''Fick's first law'': Movement of particles from high to low concentration (diffusive flux) is directly proportional to the particle's concentration gradient. ''Fick's second law'': Prediction of change in concentration gradient with time due to diffusion. A diffusion process that obeys Fick's laws is called normal or Fickian diffusion; otherwise, it is called anomalous diffusion or non-Fickian diffusion. History In 1855, physiologist Adolf Fick first reported* * his now well-known laws governing the transport of mass through diffusive means. Fick's work was inspired by the earlier experiments of Thomas Graham, which fell short of proposing the fundamental laws for which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lawrence Stamper Darken
Lawrence Stamper Darken (18 Sept. 1909, Brooklyn NY – 7 June 1978, State College PA) was an American physical chemist and metallurgist, known for his two equations describing solid-state diffusion in binary solutions. He earned his bachelor's degree in mathematics and chemistry from Hamilton College and attained his doctoral degree in physical chemistry at Yale in 1933,Dr. Lawrence S. Darken, 68, Ex.Professor of Mineral Science New York Times, 12 June 1978 followed by two postdoctoral years. From 1935 to 1971 Darken was employed at Corporation Research Laboratory where he was director of the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |