|
Closure Problem
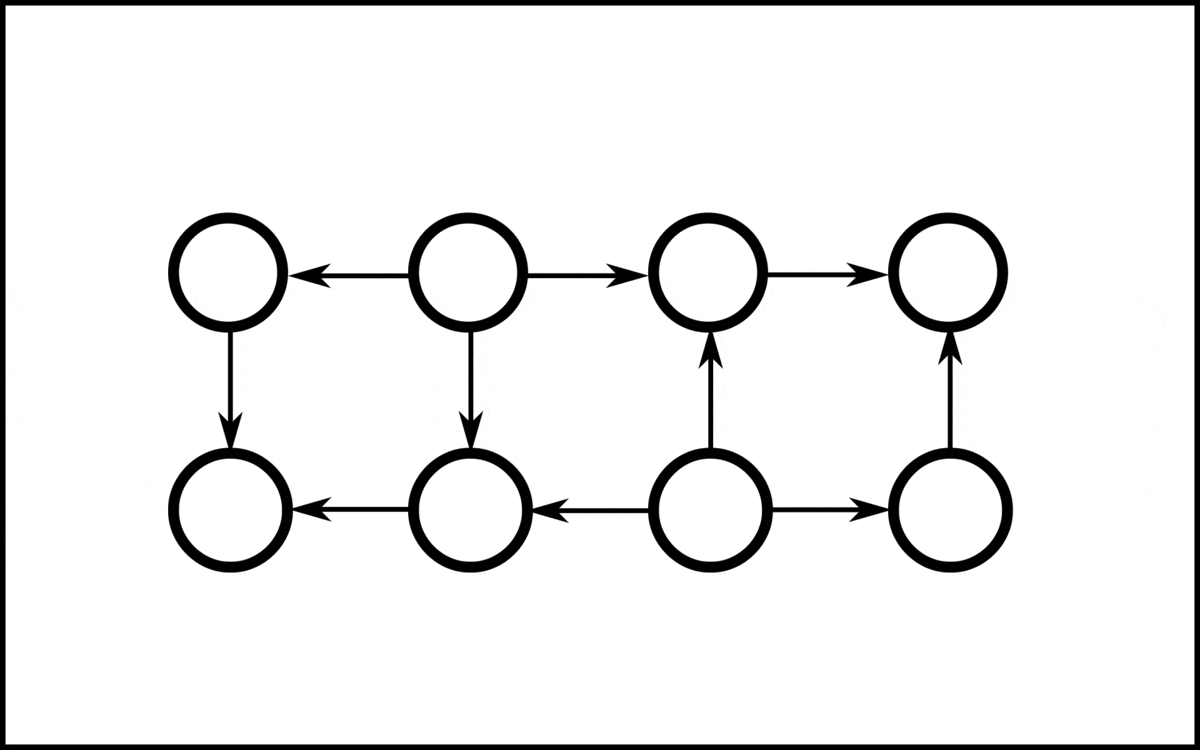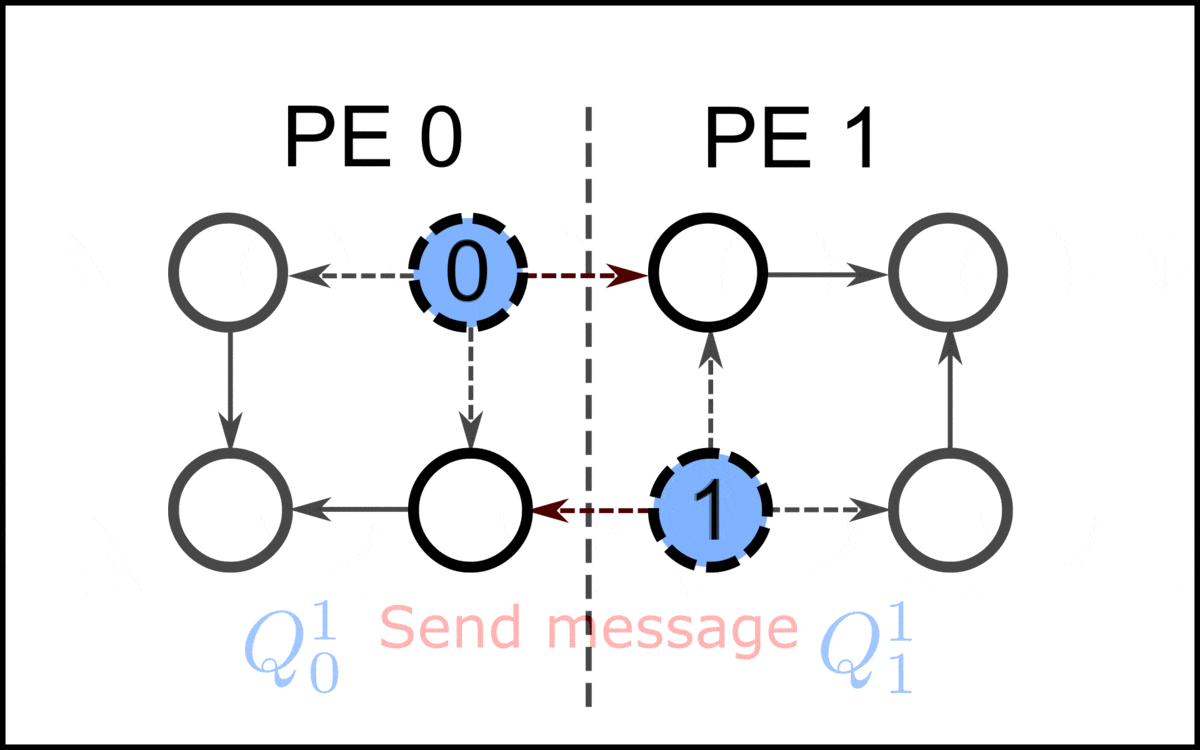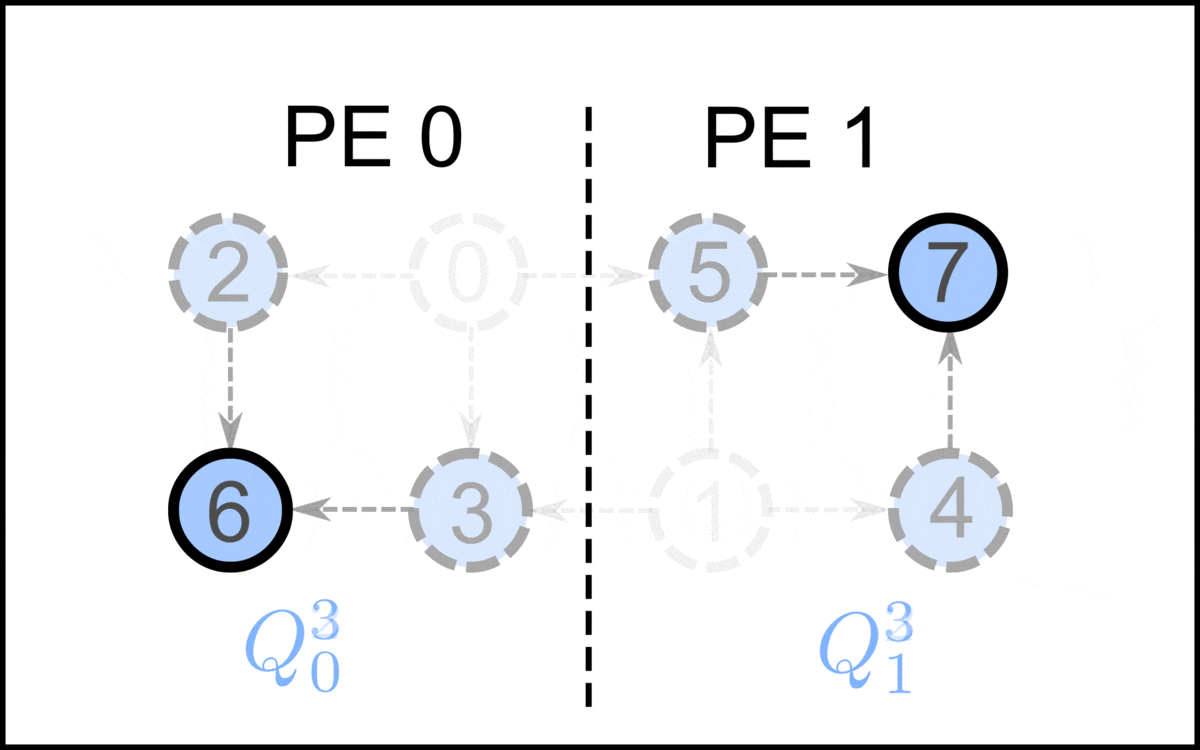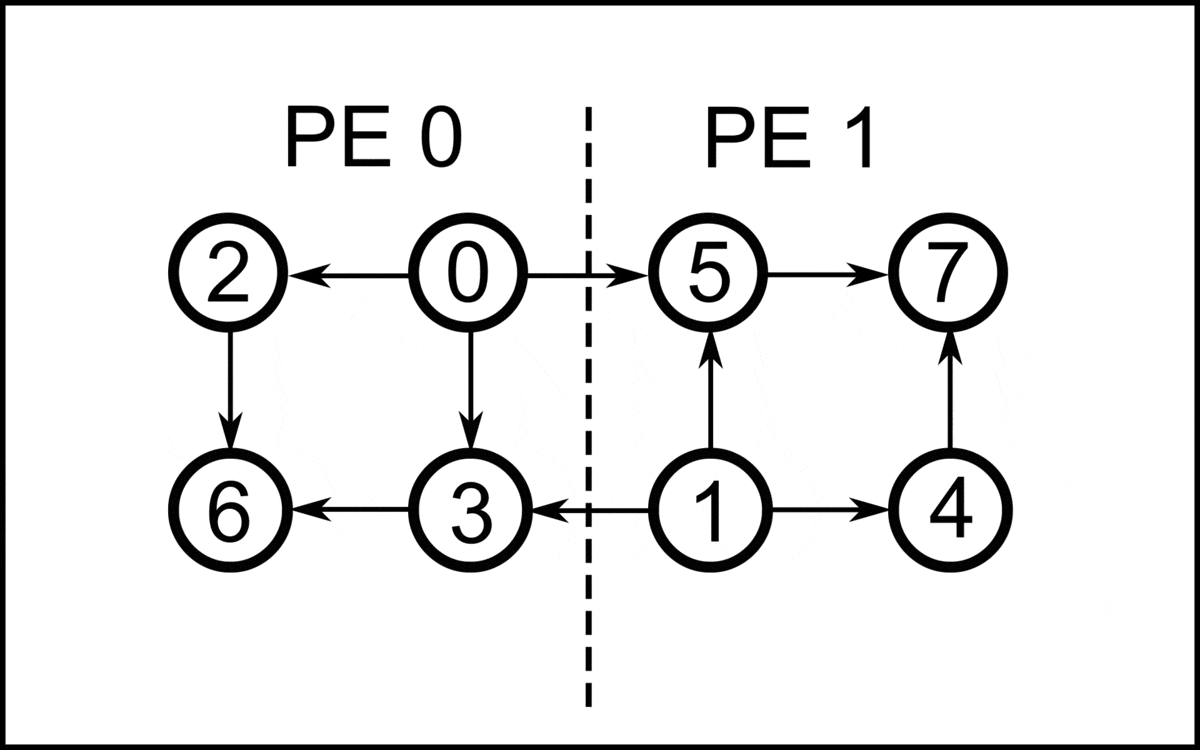
In graph theory and combinatorial optimization, a closure of a directed graph is a set of vertices ''C'', such that no edges leave ''C''. The closure problem is the task of finding the maximum-weight or minimum-weight closure in a vertex-weighted directed graph... It may be solved in polynomial time using a reduction to the maximum flow problem. It may be used to model various application problems of choosing an optimal subset of tasks to perform, with dependencies between pairs of tasks, one example being in open pit mining. Algorithms Condensation The maximum-weight closure of a given graph ''G'' is the same as the complement of the minimum-weight closure on the transpose graph of ''G'', so the two problems are equivalent in computational complexity. If two vertices of the graph belong to the same strongly connected component, they must behave the same as each other with respect to all closures: it is not possible for a closure to contain one vertex without containing the other. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph theory), vertices'' (also called ''nodes'' or ''points'') which are connected by ''Glossary of graph theory terms#edge, edges'' (also called ''arcs'', ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a Set (mathematics), set of vertices (also called nodes or points); * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimum Cut
In graph theory, a minimum cut or min-cut of a graph is a cut (a partition of the vertices of a graph into two disjoint subsets) that is minimal in some metric. Variations of the minimum cut problem consider weighted graphs, directed graphs, terminals, and partitioning the vertices into more than two sets. The weighted min-cut problem allowing both positive and negative weights can be trivially transformed into a weighted maximum cut problem by flipping the sign in all weights. __TOC__ Without terminal nodes The minimum cut problem in undirected, weighted graphs limited to non-negative weights can be solved in polynomial time by the Stoer-Wagner algorithm. In the special case when the graph is unweighted, Karger's algorithm provides an efficient randomized method for finding the cut. In this case, the minimum cut equals the edge connectivity of the graph. A generalization of the minimum cut problem without terminals is the minimum -cut, in which the goal is to partition th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mineral Economics
Mineral economics is the academic discipline that investigates and promotes understanding of economic and policy issues associated with the production and use of mineral commodities. Mineral economics ��min·rəl ‚ek·ə′näm·iksis specially concerned with the analysis and understanding of mineral distribution as well as the ‘discovery, exploitation, and marketing of minerals’. Mineral economics is an academic discipline which constructs policies regarding mineral commodities and their global distribution. The discipline of mineral economics examines the success and the implications associated with the mining industry and the impact the industry has on the economy socially and regarding the climate. Mineral economics is a continuing, evolving field which originally started after the Second World War and has continued to expand in today's modern climate. The identification of mineral sectors and their associated total revenue from specific commodities and how this varies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Search
In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array. Binary search runs in Time complexity#Logarithmic time, logarithmic time in the Best, worst and average case, worst case, making O(\log n) comparisons, where n is the number of elements in the array. Binary search is faster than linear search except for small arrays. However, the array must be sorted first to be able to apply binary search. There are specialized data structures designed fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
NP-complete
In computational complexity theory, NP-complete problems are the hardest of the problems to which ''solutions'' can be verified ''quickly''. Somewhat more precisely, a problem is NP-complete when: # It is a decision problem, meaning that for any input to the problem, the output is either "yes" or "no". # When the answer is "yes", this can be demonstrated through the existence of a short (polynomial length) ''solution''. # The correctness of each solution can be verified quickly (namely, in polynomial time) and a brute-force search algorithm can find a solution by trying all possible solutions. # The problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. Hence, if we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified. The name "NP-complete" is short for "nondeterministic polynomial-time complete". In this name, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operations Research (journal)
''Operations Research'' is a bimonthly peer-reviewed academic journal covering operations research that is published by the Institute for Operations Research and the Management Sciences. It was established in 1952 as the ''Journal of the Operations Research Society of America'' and obtained its current name in 1955. The editor-in-chief is Amy Ward (University of Chicago). Abstracting and indexing The journal is abstracted and indexed by ''Mathematical Reviews'', MathSciNet, Science Citation Index Expanded, Scopus, Social Sciences Citation Index, and ''Zentralblatt MATH''. According to the ''Journal Citation Reports'', the journal has a 2018 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with higher impact factor values are considered more prestigious or important within their field. The Impact Factor of a journa ... of 2.604. References External links * Operations research journals Academ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Job Shop Scheduling
Job-shop scheduling, the job-shop problem (JSP) or job-shop scheduling problem (JSSP) is an optimization problem in computer science and operations research. It is a variant of optimal job scheduling. In a general job scheduling problem, we are given ''n'' jobs ''J''1, ''J''2, ..., ''Jn'' of varying processing times, which need to be scheduled on ''m'' machines with varying processing power, while trying to minimize the makespan – the total length of the schedule (that is, when all the jobs have finished processing). In the specific variant known as ''job-shop scheduling'', each job consists of a set of ''operations'' ''O''1, ''O''2, ..., ''On'' which need to be processed in a specific order (known as ''precedence constraints''). Each operation has a ''specific machine'' that it needs to be processed on and only one operation in a job can be processed at a given time. A common relaxation is the flexible job shop, where each operation can be processed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Michel Balinski
Michel Louis Balinski (born Michał Ludwik Baliński; October 6, 1933 – February 4, 2019) was an American and French applied mathematician, economist, operations research analyst and political scientist. Educated in the United States, from 1980 he lived and worked in France. He was known for his work in optimisation (combinatorial, linear, nonlinear), convex polyhedra, stable matching, and the theory and practice of electoral systems, jury decision, and social choice. He was Directeur de Recherche de classe exceptionnelle (emeritus) of the C.N.R.S. at the École Polytechnique (Paris). He was awarded the John von Neumann Theory Prize by INFORMS in 2013. Michel Louis Balinski died in Bayonne, France. He maintained an active involvement in research and public appearances, his last public engagement took place in January 2019. Early life Michel Balinski was born in Geneva, Switzerland, the grandson of the Polish bacteriologist and founder of UNICEF, Ludwik Rajchman. Brought up ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Ordering
In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge ''(u,v)'' from vertex ''u'' to vertex ''v'', ''u'' comes before ''v'' in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node ''v'' is visited only after all its dependencies are visited''.'' A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and there are linear time algorithms for constructing it. Topological sorting has many applications, especially in ranking problems such as feedback arc set. Topological sorting is also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Max-flow Min-cut Theorem
In computer science and optimization theory, the max-flow min-cut theorem states that in a flow network, the maximum amount of flow passing from the ''source'' to the ''sink'' is equal to the total weight of the edges in a minimum cut, i.e., the smallest total weight of the edges which if removed would disconnect the source from the sink. For example, imagine a network of pipes carrying water from a reservoir (the source) to a city (the sink). Each pipe has a capacity representing the maximum amount of water that can flow through it per unit of time. The max-flow min-cut theorem tells us that the maximum amount of water that can reach the city is limited by the smallest total capacity of any set of pipes that, if cut, would completely isolate the reservoir from the city. This smallest total capacity is the min-cut. So, if there's a bottleneck in the pipe network, represented by a small min-cut, that bottleneck will determine the overall maximum flow of water to the city. This is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Management Science (journal)
''Management Science'' is a peer-reviewed academic journal that covers research on all aspects of management related to strategy, entrepreneurship, innovation, information technology, and organizations as well as all functional areas of business, such as accounting, finance, marketing, and operations. It is published by the Institute for Operations Research and the Management Sciences and was established in 1954 by the institute's precursor, the Institute of Management Sciences. C. West Churchman was the founding editor-in-chief. According to the ''Journal Citation Reports'', the journal has a 2022 impact factor of 5.4. Editors-in-chief The following persons are, or have been, editors-in-chief: *2018–2023: David Simchi-Levi *2014–2018: Teck-Hua Ho *2009–2014: Gérard Cachon *2003–2008: Wallace Hopp *1997–2002: Hau L. Lee *1993–1997: Gabriel R. Bitran *1983–1990: Donald G. Morrison *1968–1983: Martin K. Starr *1960–1967: Robert M. Thrall *1954–1960: C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorial Optimization
Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combinatorial optimization problems are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem. In many such problems, such as the ones previously mentioned, exhaustive search is not tractable, and so specialized algorithms that quickly rule out large parts of the search space or approximation algorithms must be resorted to instead. Combinatorial optimization is related to operations research, algorithm theory, and computational complexity theory. It has important applications in several fields, including artificial intelligence, machine learning, auction theory, software engineering, VLSI, applied mathematics and theoretical computer science. Applications Basic applications of combina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |