|
Square Enix People
In geometry, a square is a regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal sides. As with all rectangles, a square's angles are right angles (90 degrees, or /2 radians), making adjacent sides perpendicular. The area of a square is the side length multiplied by itself, and so in algebra, multiplying a number by itself is called squaring. Equal squares can tile the plane edge-to-edge in the square tiling. Square tilings are ubiquitous in tiled floors and walls, graph paper, image pixels, and game boards. Square shapes are also often seen in building floor plans, origami paper, food servings, in graphic design and heraldry, and in instant photos and fine art. The formula for the area of a square forms the basis of the calculation of area and motivates the search for methods for squaring the circle by compass and straightedge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrilateral
In Euclidean geometry, geometry a quadrilateral is a four-sided polygon, having four Edge (geometry), edges (sides) and four Vertex (geometry), corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons (e.g. pentagon). Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices A, B, C and D is sometimes denoted as \square ABCD. Quadrilaterals are either simple polygon, simple (not self-intersecting), or complex polygon, complex (self-intersecting, or crossed). Simple quadrilaterals are either convex polygon, convex or concave polygon, concave. The Internal and external angle, interior angles of a simple (and Plane (geometry), planar) quadrilateral ''ABCD'' add up to 360 Degree (angle), degrees, that is :\angle A+\angle B+\angle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tile
Tiles are usually thin, square or rectangular coverings manufactured from hard-wearing material such as ceramic, Rock (geology), stone, metal, baked clay, or even glass. They are generally fixed in place in an array to cover roofs, floors, walls, edges, or other objects such as tabletops. Alternatively, tile can sometimes refer to similar units made from lightweight materials such as perlite, wood, and mineral wool, typically used for wall and ceiling applications. In another sense, a tile is a construction tile or similar object, such as rectangular counters used in playing games (see tile-based game). The word is derived from the French Language, French word ''tuile'', which is, in turn, from the Latin Language, Latin word ''tegula'', meaning a roof tile composed of fired clay. Tiles are often used to form wall and floor coverings, and can range from simple square tiles to complex or mosaics. Tiles are most often made of pottery, ceramic, typically Ceramic glaze, glazed for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular oriented lines, called '' coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the '' origin'' and has as coordinates. The axes directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any dimension . These coordinates are the signed distances from the point to mutually perpendicular fixed h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
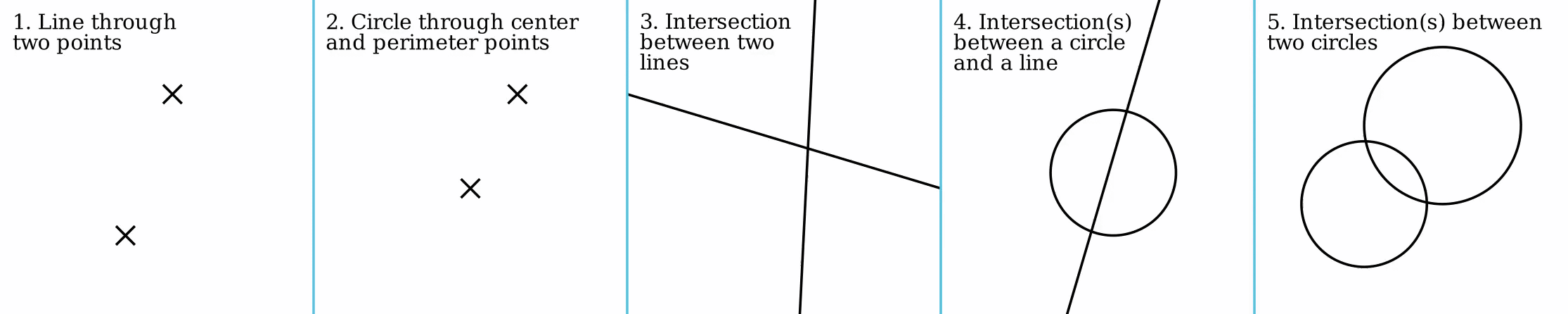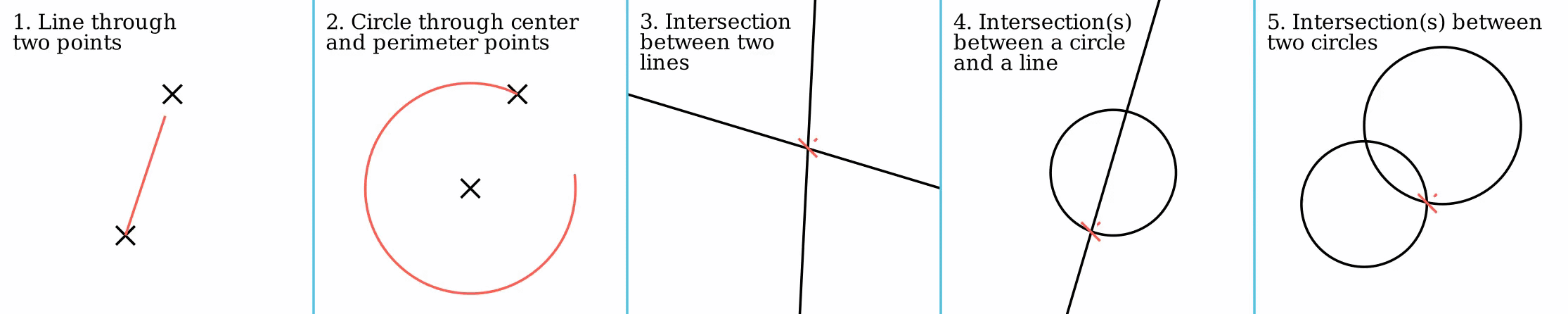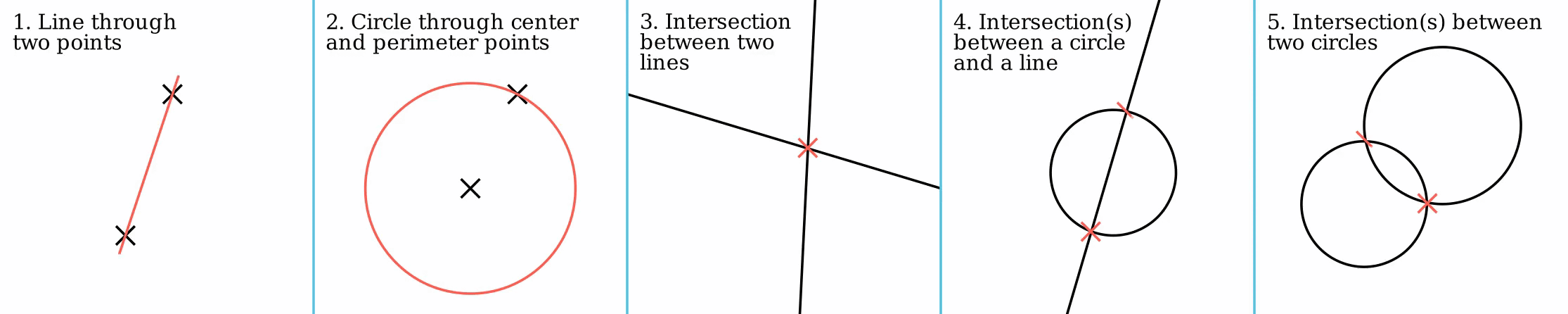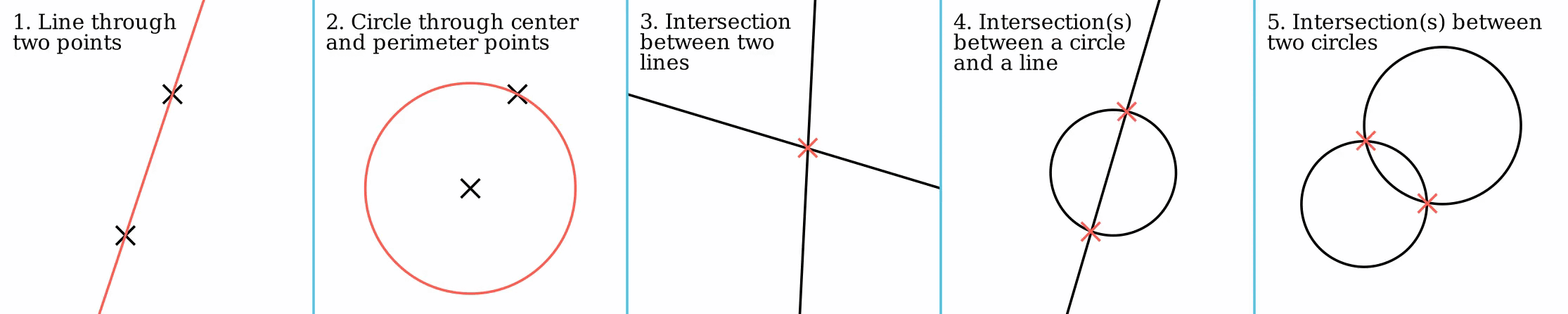
Straightedge And Compass
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a compass. The idealized ruler, known as a straightedge, is assumed to be infinite in length, have only one edge, and no markings on it. The compass is assumed to have no maximum or minimum radius, and is assumed to "collapse" when lifted from the page, so it may not be directly used to transfer distances. (This is an unimportant restriction since, using a multi-step procedure, a distance can be transferred even with a collapsing compass; see compass equivalence theorem. Note however that whilst a non-collapsing compass held against a straightedge might seem to be equivalent to marking it, the neusis construction is still impermissible and this is what unmarked really means: see Markable rulers below.) More formally, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Squaring The Square
Squaring the square is the problem of tessellation, tiling an integral square using only other integral squares. (An integral square is a square (geometry), square whose sides have integer length.) The name was coined in a humorous analogy with squaring the circle. Squaring the square is an easy task unless additional conditions are set. The most studied restriction is that the squaring be perfect, meaning the sizes of the smaller squares are all different. A related problem is squaring the plane, which can be done even with the restriction that each natural number occurs exactly once as a size of a square in the tiling. The order of a squared square is its number of constituent squares. Perfect squared squares A "perfect" squared square is a square such that each of the smaller squares has a different size. Perfect squared squares were studied by R. Leonard Brooks, R. L. Brooks, Cedric Smith (statistician), C. A. B. Smith, Arthur Harold Stone, A. H. Stone and W. T. Tutte (wr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inscribed Square Problem
The inscribed square problem, also known as the square peg problem or the Toeplitz conjecture, is an unsolved question in geometry: ''Does every plane simple closed curve contain all four vertices of some square?'' This is true if the curve is convex or piecewise smooth and in other special cases. The problem was proposed by Otto Toeplitz in 1911. Some early positive results were obtained by Arnold Emch and Lev Schnirelmann. The general case remains open. Problem statement Let C be a Jordan curve. A polygon P is inscribed in C if all vertices of P belong to C. The inscribed square problem asks: : ''Does every Jordan curve admit an inscribed square?'' It is ''not'' required that the vertices of the square appear along the curve in any particular order. Examples Some figures, such as circles and squares, admit infinitely many inscribed squares. There is one inscribed square in a triangle for any obtuse triangle, two squares for any right triangle, and three squares ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compass And Straightedge
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an Idealization (science philosophy), idealized ruler and a Compass (drawing tool), compass. The idealized ruler, known as a straightedge, is assumed to be infinite in length, have only one edge, and no markings on it. The compass is assumed to have no maximum or minimum radius, and is assumed to "collapse" when lifted from the page, so it may not be directly used to transfer distances. (This is an unimportant restriction since, using a multi-step procedure, a distance can be transferred even with a collapsing compass; see compass equivalence theorem. Note however that whilst a non-collapsing compass held against a straightedge might seem to be equivalent to marking it, the neusis construction is still impermissible and this is what unmarked really ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Squaring The Circle
Squaring the circle is a problem in geometry first proposed in Greek mathematics. It is the challenge of constructing a square (geometry), square with the area of a circle, area of a given circle by using only a finite number of steps with a compass and straightedge. The difficulty of the problem raised the question of whether specified axioms of Euclidean geometry concerning the existence of Line (geometry), lines and circles implied the existence of such a square. In 1882, the task was proven to be impossible, as a consequence of the Lindemann–Weierstrass theorem, which proves that pi (\pi) is a transcendental number. That is, \pi is not the zero of a function, root of any polynomial with Rational number, rational coefficients. It had been known for decades that the construction would be impossible if \pi were transcendental, but that fact was not proven until 1882. Approximate constructions with any given non-perfect accuracy exist, and many such constructions have been f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heraldry
Heraldry is a discipline relating to the design, display and study of armorial bearings (known as armory), as well as related disciplines, such as vexillology, together with the study of ceremony, Imperial, royal and noble ranks, rank and genealogy, pedigree. Armory, the best-known branch of heraldry, concerns the design and transmission of the Achievement (heraldry), heraldic achievement. The achievement, or armorial bearings usually includes a coat of arms on a escutcheon (heraldry), shield, helmet (heraldry), helmet and Crest (heraldry), crest, together with any accompanying devices, such as supporters, Heraldic badge, badges, Heraldic flag, heraldic banners and mottoes. Although the use of various devices to signify individuals and groups goes back to Ancient history, antiquity, both the form and use of such devices varied widely, as the concept of regular, hereditary designs, constituting the distinguishing feature of heraldry, did not develop until the High Middle Ages. It i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graphic Design
Graphic design is a profession, academic discipline and applied art that involves creating visual communications intended to transmit specific messages to social groups, with specific objectives. Graphic design is an interdisciplinary branch of design and of the fine arts. Its practice involves creativity, innovation and lateral thinking using manual or Computer-aided design, digital tools, where it is usual to use text and graphics to communicate visually. The role of the graphic designer in the communication process is that of the encoder or interpreter of the message. They work on the interpretation, ordering, and presentation of visual messages. In its nature, design pieces can be philosophical, aesthetic, emotional and political. Usually, graphic design uses the aesthetics of typography and the compositional arrangement of the text, ornamentation, and imagery to convey ideas, feelings, and attitudes beyond what language alone expresses. The design work can be based on a cust ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Origami Paper
Origami paper is the paper used for ''origami'', the art of Japanese paper folding. The only real requirement of the folding medium is that it must be able to hold a crease, but should ideally also be thinner than regular paper for convenience when multiple folds over the same small paper area are required (e.g. such as would be the case if creating an origami bird's "legs", "feet", and "beak"). Kami Kami, or koiy paper, is the cheapest paper made specifically for origami, and the most widely available. It was developed for use in schools. The word ''kami'' is simply Japanese for ''paper'', but it has acquired this specific meaning. Kami is thin and easy to fold. It is usually printed only on one side, with a solid color or pattern. These patterns can be as simple as a gradation from red to blue, or as complex as a multi-colored kimono pattern of flowers and cranes with gold foil embellishments. Kami comes in several sizes, but standard sizes include 75 × 75 mm ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
