|
Prismatoid Polyhedra
In geometry, a prismatoid is a polyhedron whose vertex (geometry), vertices all lie in two parallel Plane (geometry), planes. Its lateral faces can be trapezoids or triangles. If both planes have the same number of vertices, and the lateral faces are either parallelograms or trapezoids, it is called a prismoid. Volume If the areas of the two parallel faces are and , the cross-sectional area of the intersection of the prismatoid with a plane midway between the two parallel faces is , and the height (the distance between the two parallel faces) is , then the volume of the prismatoid is given by V = \frac. This formula follows immediately by integral, integrating the area parallel to the two planes of vertices by Simpson's rule, since that rule is exact for integration of polynomials of degree up to 3, and in this case the area is at most a quadratic function in the height. Prismatoid families Families of prismatoids include: *Pyramid (geometry), Pyramids, in which one plane con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
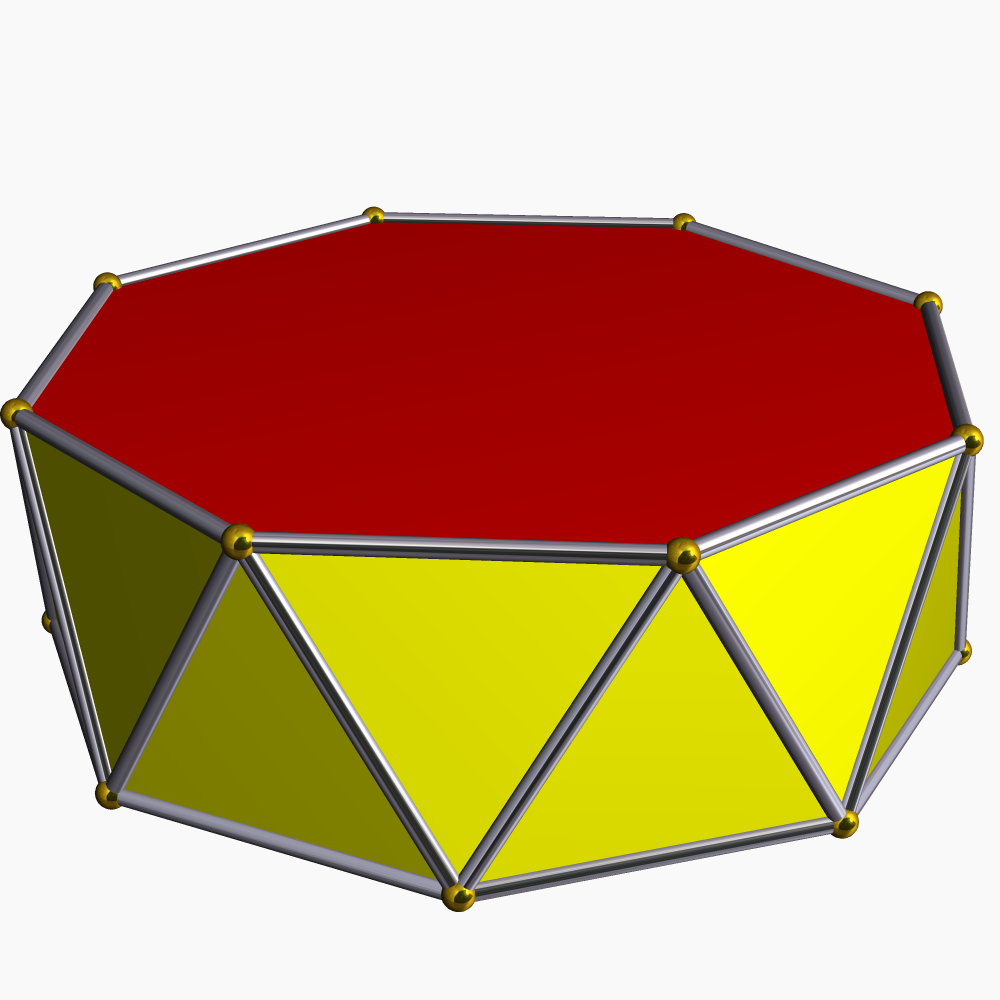
Antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway polyhedron notation, Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to Prism (geometry), prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History In his 1619 book ''Harmonices Mundi'', Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net (geometry), net of a hexagonal antiprism has been attributed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cupola (geometry)
In geometry, a cupola is a Polyhedron, solid formed by joining two polygons, one (the base) with twice as many Edge (geometry), edges as the other, by an alternating band of isosceles triangles and rectangles. If the triangles are equilateral triangle, equilateral and the rectangles are Square (geometry), squares, while the base and its opposite face are regular polygons, the triangular cupola, triangular, square cupola, square, and pentagonal cupola, pentagonal cupolae all count among the Johnson solids, and can be formed by taking sections of the cuboctahedron, rhombicuboctahedron, and rhombicosidodecahedron, respectively. A cupola can be seen as a prism (geometry), prism where one of the polygons has been collapsed in half by merging alternate vertices. A cupola can be given an extended Schläfli symbol representing a regular polygon joined by a parallel of its Truncation (geometry)#Truncation of polygons, truncation, or Cupolae are a subclass of the prismatoids. Its d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Star Antiprism
In geometry, an antiprism or is a polyhedron composed of two parallel direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History In his 1619 book ''Harmonices Mundi'', Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net of a hexagonal antiprism has been attributed to Hieronymus Andreae, who died in 1556. The German form of the word "antiprism" was used for th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Frustum
In geometry, a pentagon () is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°. A pentagon may be simple or self-intersecting. A self-intersecting ''regular pentagon'' (or ''star pentagon'') is called a pentagram. Regular pentagons A '' regular pentagon'' has Schläfli symbol and interior angles of 108°. A '' regular pentagon'' has five lines of reflectional symmetry, and rotational symmetry of order 5 (through 72°, 144°, 216° and 288°). The diagonals of a convex regular pentagon are in the golden ratio to its sides. Given its side length t, its height H (distance from one side to the opposite vertex), width W (distance between two farthest separated points, which equals the diagonal length D) and circumradius R are given by: :\begin H &= \frac~t \approx 1.539~t, \\ W= D &= \frac~t\approx 1.618~t, \\ W &= \sqrt \cdot H\approx 1.051~H, \\ R &= \sqrt t\approx 0.8507~t, \\ D &= R\ = 2R\cos 18^\circ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Cupola
Properties The pentagonal cupola (geometry), cupola's faces are five equilateral triangles, five squares, one regular pentagon, and one regular decagon. It has the property of Convex set, convexity and regular polygonal faces, from which it is classified as the fifth Johnson solid. This cupola produces two or more regular polyhedrons by slicing it with a plane, an elementary polyhedron's example. The following formulae for circumscribed sphere, circumradius R , and height h , surface area A , and volume V may be applied if all face (geometry), faces are regular polygon, regular with edge length a : \begin h &= \sqrta &\approx 0.526a, \\ R &= \fraca &\approx 2.233a, \\ A &= \fraca^2 &\approx 16.580a^2, \\ V &= \fraca^3 &\approx 2.324a^3. \end It has an axis of symmetry passing through the center of both top and base, which is symmetrical by rotating around it at one-, two-, three-, and four-fifth of a full-turn angle. It is also mirror-symmetric relative to any per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagrammic Crossed Antiprism
In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams. It differs from the pentagrammic antiprism by having opposite orientations on the two pentagrams. This polyhedron is identified with the indexed name U80 as a uniform polyhedron. The pentagrammic crossed-antiprism may be inscribed within an icosahedron, and has ten triangular faces in common with the great icosahedron. It has the same vertex arrangement as the pentagonal antiprism. In fact, it may be considered as a parabidiminished great icosahedron. See also * Prismatic uniform polyhedron External links * *http://www.mathconsult.ch/showroom/unipoly/80.html * http://bulatov.org/polyhedra/uniform/u05.html * https://web.archive.org/web/20050313234519/http://www.math.technion.ac.il/~rl/kaleido/data/05.html Prismatoid polyhedra {{Polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Antiprism
In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of ten triangles for a total of twelve faces. Hence, it is a non-regular dodecahedron. Geometry If the faces of the pentagonal antiprism are all regular, it is a semiregular polyhedron. It can also be considered as a parabidiminished icosahedron, a shape formed by removing two pentagonal pyramids from a regular icosahedron leaving two nonadjacent pentagonal faces; a related shape, the metabidiminished icosahedron (one of the Johnson solids), is likewise form from the icosahedron by removing two pyramids, but its pentagonal faces are adjacent to each other. The two pentagonal faces of either shape can be augmented with pyramids to form the icosahedron. The semiregular pentagonal antiprism is inscribed in a cylinder whose bases are the disks in which the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Antiprism
In geometry, the square antiprism is the second in an infinite family of antiprisms formed by an even number, even-numbered sequence of triangle sides closed by two polygon caps. It is also known as an ''anticube''. If all its faces are regular polygon, regular, it is a semiregular polyhedron or uniform polyhedron. A nonuniform ''D''4-symmetric variant is the cell of the Noble polyhedron, noble square antiprismatic 72-cell. Points on a sphere When eight points are distributed on the surface of a sphere with the aim of maximising the distance between them in some sense, the resulting shape corresponds to a square antiprism rather than a cube (geometry), cube. Specific methods of distributing the points include, for example, the Thomson problem (minimizing the sum of all the reciprocal (mathematics), reciprocals of distances between points), maximising the distance of each point to the nearest point, or minimising the sum of all reciprocals of squares of distances between points ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Prism
In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with seven faces, fifteen edges, and ten vertices. As a semiregular (or uniform) polyhedron If faces are all regular, the pentagonal prism is a semiregular polyhedron, more generally, a uniform polyhedron, and the third in an infinite set of prisms formed by square sides and two regular polygon caps. It can be seen as a '' truncated pentagonal hosohedron'', represented by Schläfli symbol t. Alternately it can be seen as the Cartesian product of a regular pentagon and a line segment, and represented by the product ×. The dual of a pentagonal prism is a pentagonal bipyramid. The symmetry group of a right pentagonal prism is ''D5h'' of order 20. The rotation group is ''D5'' of order 10. Volume The volume, as for all prisms, is the product of the area of the pentagonal base times the height or distance along any edge perpendicular to the base. For a uniform pentagonal prism ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelepiped 2013-11-29
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term ''rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square. Three equivalent definitions of ''parallelepiped'' are *a hexahedron with three pairs of parallel faces, *a polyhedron with six faces (hexahedron), each of which is a parallelogram, and *a prism of which the base is a parallelogram. The rectangular cuboid (six rectangular faces), cube (six square faces), and the rhombohedron (six rhombus faces) are all special cases of parallelepiped. "Parallelepiped" is now usually pronounced or ; traditionally it was because of its etymology in Greek παραλληλεπίπεδον ''parallelepipedon'' (with short -i-), a body "having parallel planes". Parallelepipeds are a subclass of the prismatoids. Properties Any of the three pairs of parallel faces can be viewed as the base planes of the prism. A parall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Wedge
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |