|
Periodic Phenomena
Periodicity or periodic may refer to: Mathematics * Bott periodicity theorem, addresses Bott periodicity: a modulo-8 recurrence relation in the homotopy groups of classical groups * Periodic function, a function whose output contains values that repeat periodically * Periodic mapping Physical sciences * Periodic table of chemical elements * Periodic trends, relative characteristics of chemical elements observed * Redshift periodicity, astronomical term for redshift quantization Other uses * Fokker periodicity blocks, which mathematically relate musical intervals * Periodic acid, a compound of iodine * Principle of periodicity, a concept in generally accepted accounting principles * Quasiperiodicity, property of a system that displays irregular periodicity See also * Aperiodic (other) * Cycle (other) * Frequency (other) * Period (other) * Periodical * Seasonality, periodic variation, or periodic fluctuations {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bott Periodicity Theorem
In mathematics, the Bott periodicity theorem describes a periodicity in the homotopy groups of classical groups, discovered by , which proved to be of foundational significance for much further research, in particular in K-theory of stable complex vector bundles, as well as the stable homotopy groups of spheres. Bott periodicity can be formulated in numerous ways, with the periodicity in question always appearing as a period-2 phenomenon, with respect to dimension, for the theory associated to the unitary group. See for example topological K-theory. There are corresponding period-8 phenomena for the matching theories, (real number, real) KO-theory and (quaternionic) KSp-theory, associated to the real orthogonal group and the quaternionic symplectic group, respectively. The J-homomorphism is a homomorphism from the homotopy groups of orthogonal groups to stable homotopy groups of spheres, which causes the period 8 Bott periodicity to be visible in the stable homotopy groups of sph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Function
A periodic function, also called a periodic waveform (or simply periodic wave), is a function that repeats its values at regular intervals or periods. The repeatable part of the function or waveform is called a ''cycle''. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function that is not periodic is called ''aperiodic''. Definition A function is said to be periodic if, for some nonzero constant , it is the case that :f(x+P) = f(x) for all values of in the domain. A nonzero constant for which this is the case is called a period of the function. If there exists a least positive constant with this property, it is called the fundamental period (also primitive period, basic period, or prime period.) Often, "the" period of a function is used to mean its fundamental period. A funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Mapping
In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time. Iterated functions Given a mapping from a set into itself, :f: X \to X, a point in is called periodic point if there exists an >0 so that :\ f_n(x) = x where is the th iterate of . The smallest positive integer satisfying the above is called the ''prime period'' or ''least period'' of the point . If every point in is a periodic point with the same period , then is called ''periodic'' with period (this is not to be confused with the notion of a periodic function). If there exist distinct and such that :f_n(x) = f_m(x) then is called a preperiodic point. All periodic points are preperiodic. If is a diffeomorphism of a differentiable manifold In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
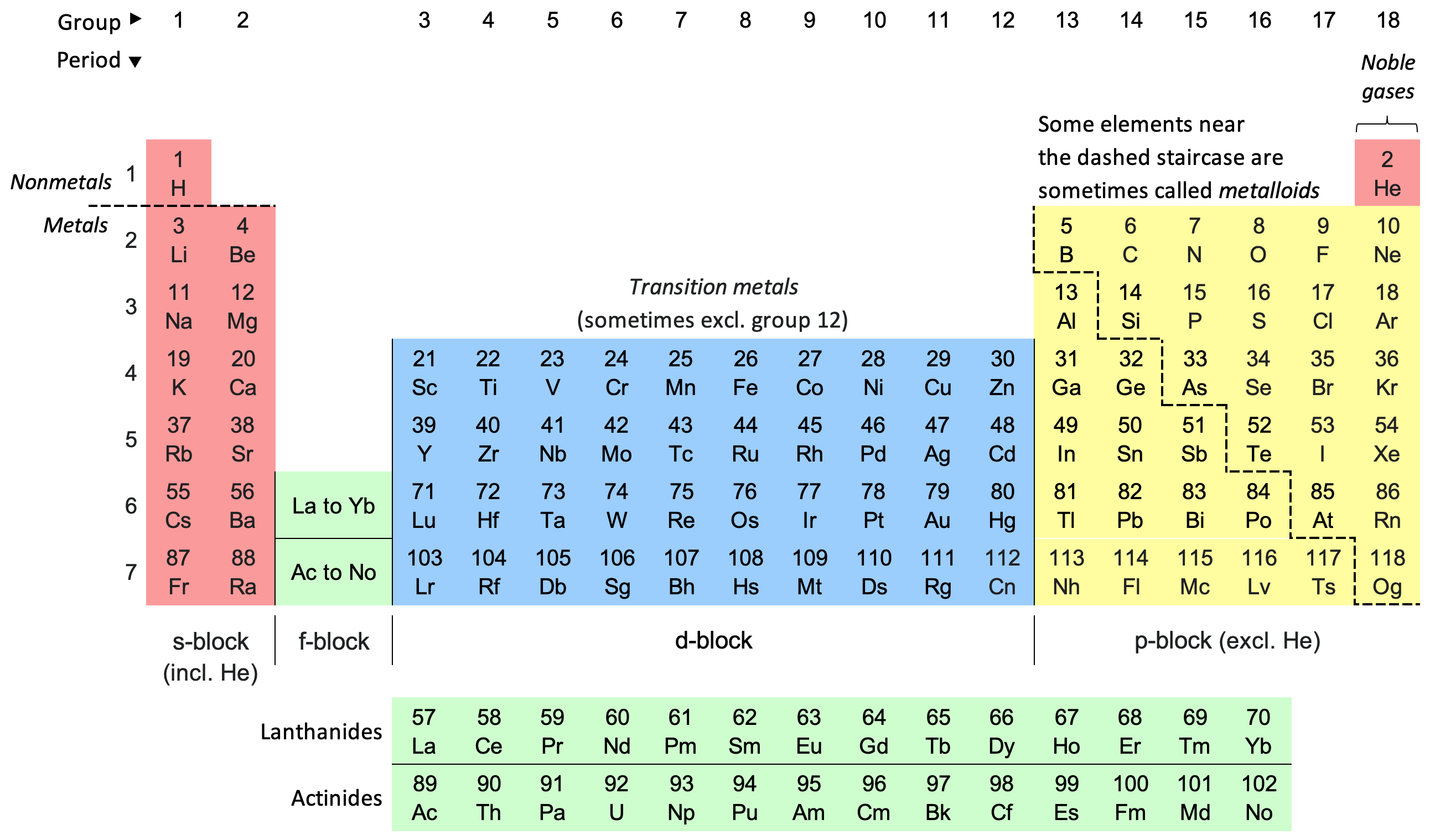
Periodic Table
The periodic table, also known as the periodic table of the elements, is an ordered arrangement of the chemical elements into rows (" periods") and columns (" groups"). It is an icon of chemistry and is widely used in physics and other sciences. It is a depiction of the periodic law, which states that when the elements are arranged in order of their atomic numbers an approximate recurrence of their properties is evident. The table is divided into four roughly rectangular areas called blocks. Elements in the same group tend to show similar chemical characteristics. Vertical, horizontal and diagonal trends characterize the periodic table. Metallic character increases going down a group and from right to left across a period. Nonmetallic character increases going from the bottom left of the periodic table to the top right. The first periodic table to become generally accepted was that of the Russian chemist Dmitri Mendeleev in 1869; he formulated the periodic law as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Trends
In chemistry, periodic trends are specific patterns present in the periodic table that illustrate different aspects of certain Chemical element, elements when grouped by period (periodic table), period and/or Group (periodic table), group. They were discovered by the Russian chemist Dmitri Mendeleev in 1863. Major periodic trends include atomic radius, ionization energy, electron affinity, electronegativity, nucleophilicity, electrophilicity, Valence (chemistry), valency, nuclear charge, and metal#Chemical, metallic character. Dmitri Mendeleev, Mendeleev built the foundation of the periodic table. Mendeleev organized the elements based on atomic weight, leaving empty spaces where he believed undiscovered elements would take their places. Mendeleev's discovery of this trend allowed him to predict the existence and properties of three unknown elements, which were later discovered by other chemists and named gallium, scandium, and germanium. English physicist Henry Moseley discovered ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Redshift Quantization
Redshift quantization, also referred to as redshift periodicity, redshift discretization, preferred redshifts and redshift-magnitude bands, is the hypothesis that the redshifts of cosmologically distant objects (in particular galaxies and quasars) tend to cluster around multiples of some particular value. In standard inflationary cosmological models, the redshift of cosmological bodies is ascribed to the expansion of the universe, with greater redshift indicating greater cosmic distance from the Earth (see Hubble's law). This is referred to as cosmological redshift and is one of the main pieces of evidence for the Big Bang. Quantized redshifts of objects would indicate, under Hubble's law, that astronomical objects are arranged in a quantized pattern around the Earth. It is more widely posited that the redshift is unrelated to cosmic expansion and is the outcome of some other physical mechanism, referred to as "intrinsic redshift" or "non-cosmological redshift". In 1973, as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fokker Periodicity Blocks
Fokker periodicity blocks are a concept in tuning theory used to mathematically relate musical intervals in just intonation to those in equal tuning. They are named after Adriaan Daniël Fokker. These are included as the primary subset of what Erv Wilson refers to as constant structures, where "each interval occurs always subtended by the same number of steps". The basic idea of Fokker's periodicity blocks is to represent just ratios as points on a lattice, and to find vectors in the lattice which represent very small intervals, known as commas. Treating pitches separated by a comma as equivalent "folds" the lattice, effectively reducing its dimension by one; mathematically, this corresponds to finding the quotient group of the original lattice by the sublattice generated by the commas. For an ''n''-dimensional lattice, identifying ''n'' linearly independent commas reduces the dimension of the lattice to zero, meaning that the number of pitches in the lattice is finite ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Acid
Periodic acid ( ) is an oxoacid of iodine. It can exist in two forms: orthoperiodic acid, with the chemical formula , and metaperiodic acid, which has the formula . Periodic acids are colourless crystals. Periodic acid features iodine in the highest oxidation state of +7. Periodic acid was discovered by Heinrich Gustav Magnus and C. F. Ammermüller in 1833. Synthesis Modern industrial scale production involves the oxidation of a solution of sodium iodate under Alkali, alkaline conditions, either electrochemically on a Lead dioxide, anode, or by treatment with chlorine: : (counter ions omitted for clarity) Standard electrode potential, ''E''° = −1.6 V : A standard laboratory preparation involves treating a mixture of tribarium dihydrogen orthoperiodate with nitric acid. Upon concentrating the mixture, the barium nitrate, which is less soluble, is separated from periodic acid: : Properties Orthoperiodic acid has a number of acid dissociation constants. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |