|
Linear Filters
Linear filters process time-varying input signals to produce output signals, subject to the constraint of linearity. In most cases these linear filters are also time invariant (or shift invariance, shift invariant) in which case they can be analyzed exactly using LTI system theory, LTI ("linear time-invariant") system theory revealing their transfer function#Linear time-invariant systems, transfer functions in the frequency domain and their impulse responses in the time domain. Real-time implementations of such linear signal processing filters in the time domain are inevitably causal, an additional constraint on their transfer functions. An analog electronic circuit consisting only of linear components (resistors, capacitors, inductors, and linear amplifiers) will necessarily fall in this category, as will comparable mechanical systems or digital signal processing systems containing only linear elements. Since linear time-invariant filters can be completely characterized by their r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linearity
In mathematics, the term ''linear'' is used in two distinct senses for two different properties: * linearity of a '' function'' (or '' mapping''); * linearity of a '' polynomial''. An example of a linear function is the function defined by f(x)=(ax,bx) that maps the real line to a line in the Euclidean plane R2 that passes through the origin. An example of a linear polynomial in the variables X, Y and Z is aX+bY+cZ+d. Linearity of a mapping is closely related to '' proportionality''. Examples in physics include the linear relationship of voltage and current in an electrical conductor ( Ohm's law), and the relationship of mass and weight. By contrast, more complicated relationships, such as between velocity and kinetic energy, are '' nonlinear''. Generalized for functions in more than one dimension, linearity means the property of a function of being compatible with addition and scaling, also known as the superposition principle. Linearity of a polynomial means that it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal (information Theory)
A signal is both the process and the result of Signal transmission, transmission of data over some transmission media, media accomplished by embedding some variation. Signals are important in multiple subject fields including signal processing, information theory and biology. In signal processing, a signal is a function that conveys information about a phenomenon. Any quantity that can vary over space or time can be used as a signal to share messages between observers. The ''IEEE Transactions on Signal Processing'' includes audio signal, audio, video, speech, image, sonar, and radar as examples of signals. A signal may also be defined as observable change in a quantity over space or time (a time series), even if it does not carry information. In nature, signals can be actions done by an organism to alert other organisms, ranging from the release of plant chemicals to warn nearby plants of a predator, to sounds or motions made by animals to alert other animals of food. Signa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electronic Filter
Electronic filters are a type of signal processing filter in the form of electrical circuits. This article covers those filters consisting of lumped-element model, lumped electronic components, as opposed to distributed-element filters. That is, using components and interconnections that, in analysis, can be considered to exist at a single point. These components can be in discrete packages or part of an integrated circuit. Electronic filters remove unwanted frequency components from the applied signal, enhance wanted ones, or both. They can be: *Passive filter, passive or active filter, active *analogue filter, analog or digital filter, digital *high-pass filter, high-pass, low-pass filter, low-pass, band-pass filter, band-pass, band-stop filter, band-stop (band-rejection; notch), or all-pass filter, all-pass. *discrete-time (sampled) or Continuous signal, continuous-time *linear filter, linear or non-linear filter, non-linear *infinite impulse response (IIR type) or finite ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bucket-brigade Device
A bucket brigade or bucket-brigade device (BBD) is a discrete-time analogue delay line, developed in 1969 by F. Sangster and K. Teer of the Philips Research Labs in the Netherlands. It consists of a series of capacitance sections C0 to Cn. The stored analogue signal is moved along the line of capacitors, one step at each clock cycle. The name comes from analogy with the term bucket brigade, used for a line of people passing buckets of water. In most signal processing applications, bucket brigades have been replaced by devices that use digital signal processing, manipulating samples in digital form. Bucket brigades still see use in specialty applications, such as guitar effects. A well-known integrated circuit device around 1976, the Reticon SAD-1024 implemented two 512-stage analog delay lines in a 16-pin DIP. It allowed clock frequencies ranging from 1.5 kHz to more than 1.5 MHz. The SAD-512 was a single delay line version. The Philips Semiconductors ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analog Sampled Filter
An analog sampled filter an electronic filter that is a hybrid between an analog and a digital filter. The input is an analog signal, and usually stored in capacitors. The time domain is discrete, however. Distinct analog samples are shifted through an array of holding capacitors as in a bucket brigade. Analog adders and amplifiers do the arithmetic in the signal domain, just as in an analog computer. Note that these filters are subject to aliasing phenomena just like a digital filter, and anti-aliasing filters will usually be required. See . Companies such as Linear Technology and Maxim produce integrated circuits that implement this functionality. Filters up to the 8th order may be implemented using a single chip. Some are fully configurable; some are pre-configured, usually as low-pass filters. Due to the high filter order that can be achieved in an easy and stable manner, single chip analog sampled filters are often used for implementing anti-aliasing filters for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Functions
In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be rational numbers; they may be taken in any field . In this case, one speaks of a rational function and a rational fraction ''over ''. The values of the variables may be taken in any field containing . Then the domain of the function is the set of the values of the variables for which the denominator is not zero, and the codomain is . The set of rational functions over a field is a field, the field of fractions of the ring of the polynomial functions over . Definitions A function f is called a rational function if it can be written in the form : f(x) = \frac where P and Q are polynomial functions of x and Q is not the zero function. The domain of f is the set of all values of x for which the denominator Q(x) is not zero. However, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Impulse Response
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response (or response to any finite length input) is of ''finite'' duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely (usually decaying). The impulse response (that is, the output in response to a Kronecker delta input) of an Nth-order discrete-time FIR filter lasts exactly N+1 samples (from first nonzero element through last nonzero element) before it then settles to zero. FIR filters can be discrete-time or continuous-time, and digital or analog. Definition For a causal discrete-time FIR filter of order ''N'', each value of the output sequence is a weighted sum of the most recent input values: :\begin y &= b_0 x + b_1 x -1+ \cdots + b_N x -N\\ &= \sum_^N b_i\cdot x -i \end where: * x /math> is the input signal, * y /math> is the outpu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
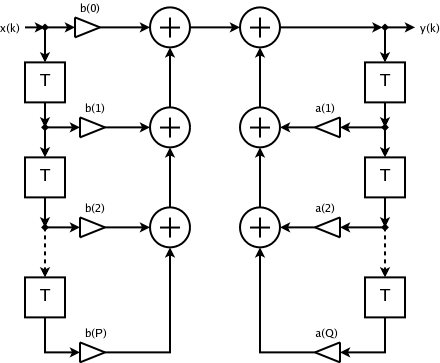
Infinite Impulse Response
Infinite impulse response (IIR) is a property applying to many linear time-invariant systems that are distinguished by having an impulse response h(t) that does not become exactly zero past a certain point but continues indefinitely. This is in contrast to a finite impulse response (FIR) system, in which the impulse response ''does'' become exactly zero at times t>T for some finite T, thus being of finite duration. Common examples of linear time-invariant systems are most electronic and digital filters. Systems with this property are known as ''IIR systems'' or ''IIR filters''. In practice, the impulse response, even of IIR systems, usually approaches zero and can be neglected past a certain point. However the physical systems which give rise to IIR or FIR responses are dissimilar, and therein lies the importance of the distinction. For instance, analog electronic filters composed of resistors, capacitors, and/or inductors (and perhaps linear amplifiers) are generally IIR filte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Of A Polynomial
In mathematics, the degree of a polynomial is the highest of the degrees of the polynomial's monomials (individual terms) with non-zero coefficients. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer. For a univariate polynomial, the degree of the polynomial is simply the highest exponent occurring in the polynomial. The term order has been used as a synonym of ''degree'' but, nowadays, may refer to several other concepts (see Order of a polynomial (other)). For example, the polynomial 7x^2y^3 + 4x - 9, which can also be written as 7x^2y^3 + 4x^1y^0 - 9x^0y^0, has three terms. The first term has a degree of 5 (the sum of the powers 2 and 3), the second term has a degree of 1, and the last term has a degree of 0. Therefore, the polynomial has a degree of 5, which is the highest degree of any term. To determine the degree of a polynomial that is not in standard form, such as (x+1)^2 - (x-1)^2, one c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sampling Period
In signal processing, sampling is the reduction of a continuous-time signal to a discrete-time signal. A common example is the conversion of a sound wave to a sequence of "samples". A sample is a value of the signal at a point in time and/or space; this definition differs from the term's usage in statistics, which refers to a set of such values. A sampler is a subsystem or operation that extracts samples from a continuous signal. A theoretical ideal sampler produces samples equivalent to the instantaneous value of the continuous signal at the desired points. The original signal can be reconstructed from a sequence of samples, up to the Nyquist limit, by passing the sequence of samples through a reconstruction filter. Theory Functions of space, time, or any other dimension can be sampled, and similarly in two or more dimensions. For functions that vary with time, let s(t) be a continuous function (or "signal") to be sampled, and let sampling be performed by measuring the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolved
In mathematics (in particular, functional analysis), convolution is a mathematical operation on two functions f and g that produces a third function f*g, as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The term ''convolution'' refers to both the resulting function and to the process of computing it. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result (see commutativity). Graphically, it expresses how the 'shape' of one function is modified by the other. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution f*g differs from cross-correlation f \star g only in that either f(x) or g(x) is reflected about the y-axis in convolution; thus it is a cross-correlation of g(-x) and f(x), or f(-x) and g(x). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superposition Principle
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So that if input ''A'' produces response ''X'', and input ''B'' produces response ''Y'', then input (''A'' + ''B'') produces response (''X'' + ''Y''). A function F(x) that satisfies the superposition principle is called a linear function. Superposition can be defined by two simpler properties: additivity F(x_1 + x_2) = F(x_1) + F(x_2) and homogeneity F(ax) = a F(x) for scalar . This principle has many applications in physics and engineering because many physical systems can be modeled as linear systems. For example, a beam can be modeled as a linear system where the input stimulus is the load on the beam and the output response is the deflection of the beam. The importance of linear systems is that they are easier to analyze mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |