|
Geometrical Optics
Geometrical optics, or ray optics, is a model of optics that describes light Wave propagation, propagation in terms of ''ray (optics), rays''. The ray in geometrical optics is an abstract object, abstraction useful for approximating the paths along which light propagates under certain circumstances. The simplifying assumptions of geometrical optics include that light rays: * propagate in straight-line paths as they travel in a Homogeneity (physics), homogeneous medium * bend, and in particular circumstances may split in two, at the Interface (matter), interface between two dissimilar optical medium, media * follow curved paths in a medium in which the refractive index changes * may be absorbed or reflected. Geometrical optics does not account for certain optical effects such as diffraction and Interference (wave propagation), interference, which are considered in physical optics. This simplification is useful in practice; it is an excellent approximation when the wavelength is smal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes the behaviour of visible light, visible, ultraviolet, and infrared light. Light is a type of electromagnetic radiation, and other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties. Most optical phenomena can be accounted for by using the Classical electromagnetism, classical electromagnetic description of light, however complete electromagnetic descriptions of light are often difficult to apply in practice. Practical optics is usually done using simplified models. The most common of these, geometric optics, treats light as a collection of Ray (optics), rays that travel in straight lines and bend when they pass through or reflect from surfaces. Physical optics is a more comprehensive mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perpendicular
In geometry, two geometric objects are perpendicular if they intersect at right angles, i.e. at an angle of 90 degrees or π/2 radians. The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', ⟂. Perpendicular intersections can happen between two lines (or two line segments), between a line and a plane, and between two planes. ''Perpendicular'' is also used as a noun: a perpendicular is a line which is perpendicular to a given line or plane. Perpendicularity is one particular instance of the more general mathematical concept of '' orthogonality''; perpendicularity is the orthogonality of classical geometric objects. Thus, in advanced mathematics, the word "perpendicular" is sometimes used to describe much more complicated geometric orthogonality conditions, such as that between a surface and its '' normal vector''. A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reflection Angles
Reflection or reflexion may refer to: Science and technology * Reflection (physics), a common wave phenomenon ** Specular reflection, mirror-like reflection of waves from a surface *** Mirror image, a reflection in a mirror or in water ** Diffuse reflection, where ray incident on the surface is scattered ** Retroreflection, technology for returning light in the direction from which it came ** Signal reflection, in signal transmission * Elastic scattering, a process in nuclear and particle physics * Reflection nebula, a nebula that is extended and has no boundaries * Reflection seismology or seismic reflection, a method of exploration geophysics Mathematics * Reflection principle, in set theory * Point reflection, a reflection across a point * Reflection (mathematics), a transformation of a space * Reflection formula, a relation in a function * Reflective subcategory, in category theory * Reflection symmetry, the property of being unchanged by a reflection Computing * Ref ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SPIE
SPIE (formerly the Society of Photographic Instrumentation Engineers, later the Society of Photo-Optical Instrumentation Engineers) is an international not-for-profit professional society for optics and photonics technology, founded in 1955. It organizes technical conferences, trade exhibitions, and continuing education programs for researchers and developers in the light-based fields of physics, including: optics, photonics, and imaging engineering. The society publishes peer-reviewed scientific journals, conference proceedings, monographs, tutorial texts, field guides, and reference volumes in print and online. SPIE is especially well-known for Photonics West, one of the laser and photonics industry's largest combined conferences and tradeshows which is held annually in San Francisco. SPIE also participates as partners in leading educational initiatives, and in 2020, for example, provided more than $5.8 million in support of optics education and outreach programs around the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnification
Magnification is the process of enlarging the apparent size, not physical size, of something. This enlargement is quantified by a size ratio called optical magnification. When this number is less than one, it refers to a reduction in size, sometimes called ''de-magnification''. Typically, magnification is related to scaling up visuals or images to be able to see more detail, increasing resolution, using microscope, printing techniques, or digital processing. In all cases, the magnification of the image does not change the perspective of the image. Examples of magnification Some optical instruments provide visual aid by magnifying small or distant subjects. * A magnifying glass, which uses a positive (convex) lens to make things look bigger by allowing the user to hold them closer to their eye. * A telescope, which uses its large objective lens or primary mirror to create an image of a distant object and then allows the user to examine the image closely with a smaller ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Image
An image or picture is a visual representation. An image can be Two-dimensional space, two-dimensional, such as a drawing, painting, or photograph, or Three-dimensional space, three-dimensional, such as a carving or sculpture. Images may be displayed through other media, including a Projector, projection on a surface, activation of electronic signals, or Display device, digital displays; they can also be reproduced through mechanical means, such as photography, printmaking, or Photocopier, photocopying. Images can also be Animation, animated through digital or physical processes. In the context of signal processing, an image is a distributed amplitude of color(s). In optics, the term ''image'' (or ''optical image'') refers specifically to the reproduction of an object formed by light waves coming from the object. A ''volatile image'' exists or is perceived only for a short period. This may be a reflection of an object by a mirror, a projection of a camera obscura, or a scene d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ray Tracing (physics)
In physics, ray tracing is a method for calculating the path of waves or Subatomic particle, particles through a system with regions of varying propagation velocity, absorption characteristics, and reflecting surfaces. Under these circumstances, wavefronts may bend, change direction, or reflection (physics), reflect off surfaces, complicating analysis. Historically, ray tracing involved analytic solutions to the ray's trajectories. In modern applied physics and engineering physics, the term also encompasses numerical solutions to the Eikonal equation. For example, Ray marching, ray-marching involves repeatedly advancing idealized narrow beams called ''ray (optics), rays'' through the medium (optics), medium by discrete amounts. Simple problems can be analyzed by propagating a few rays using simple mathematics. More detailed analysis can be performed by using a computer to propagate many rays. When applied to problems of electromagnetic radiation, ray tracing often relies on appr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Optics
Gaussian optics is a technique in geometrical optics that describes the behaviour of light rays in optical systems by using the paraxial approximation, in which only rays which make small angles with the optical axis of the system are considered. In this approximation, trigonometric functions can be expressed as linear functions of the angles. Gaussian optics applies to systems in which all the optical surfaces are either flat or are portions of a sphere. In this case, simple explicit formulae can be given for parameters of an imaging system such as focal length, magnification and brightness, in terms of the geometrical shapes and material properties of the constituent elements. Gaussian optics is named after mathematician and physicist Carl Friedrich Gauss, who showed that an optical system can be characterized by a series of Cardinal point (optics), cardinal points, which allow one to calculate its optical properties.W.J. Smith''Modern Optical Engineering'' 2007, McGraw-Hil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
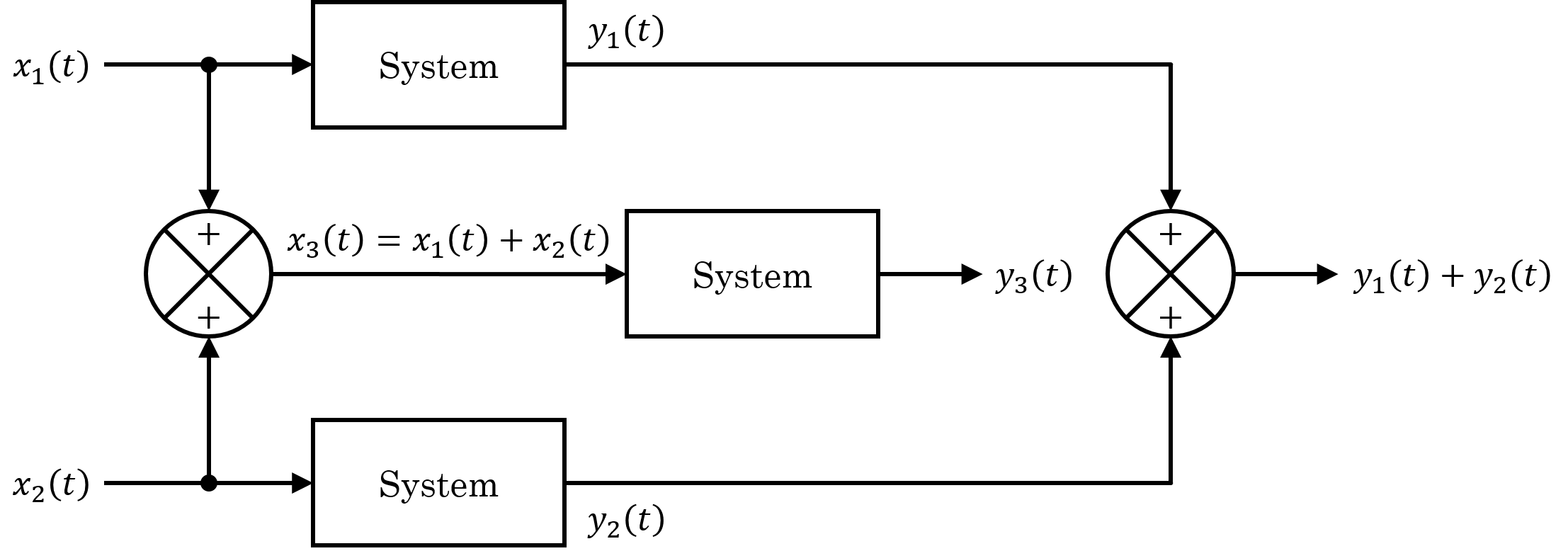
Linear System
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems. Definition A general deterministic system can be described by an operator, , that maps an input, , as a function of to an output, , a type of black box description. A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.) The superposition principle means that a linear combination of inputs to the system produces a linear com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paraxial Approximation
In geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system (such as a lens). A paraxial ray is a ray that makes a small angle (''θ'') to the optical axis of the system, and lies close to the axis throughout the system. Generally, this allows three important approximations (for ''θ'' in radians) for calculation of the ray's path, namely: : \sin \theta \approx \theta,\quad \tan \theta \approx \theta \quad \text\quad\cos \theta \approx 1. The paraxial approximation is used in Gaussian optics and ''first-order'' ray tracing. Ray transfer matrix analysis is one method that uses the approximation. In some cases, the second-order approximation is also called "paraxial". The approximations above for sine and tangent do not change for the "second-order" paraxial approximation (the second term in their Taylor series expansion is zero), while for cosine the second order approximation is : \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arthur Schuster
Sir Franz Arthur Friedrich Schuster (12 September 1851 – 14 October 1934) was a German-born British physicist known for his work in spectroscopy, electrochemistry, optics, X-radiography and the application of harmonic analysis to physics. Schuster's integral is named after him. He contributed to making the University of Manchester a centre for the study of physics. Early years Arthur Schuster was born in Frankfurt am Main, Germany the son of Francis Joseph Schuster, a cotton merchant and banker, and his wife Marie Pfeiffer. Schuster's parents were married in 1849, converted from Judaism to Christianity, and brought up their children in that faith. In 1869, his father moved to Manchester where the family textile business was based. Arthur, who had been to school in Frankfurt and was studying in Geneva, joined his parents in 1870 and he and the other children became British citizens in 1875. From his childhood, Schuster had been interested in science and after working for a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermat's Principle
Fermat's principle, also known as the principle of least time, is the link between geometrical optics, ray optics and physical optics, wave optics. Fermat's principle states that the path taken by a Ray (optics), ray between two given points is the path that can be traveled in the least time. First proposed by the French mathematician Pierre de Fermat in 1662, as a means of explaining the Snell's law, ordinary law of refraction of light (Fig.1), Fermat's principle was initially controversial because it seemed to ascribe knowledge and intent to nature. Not until the 19th century was it understood that nature's ability to test alternative paths is merely a fundamental property of waves. If points ''A'' and ''B'' are given, a wavefront expanding from ''A'' sweeps all possible ray paths radiating from ''A'', whether they pass through ''B'' or not. If the wavefront reaches point ''B'', it sweeps not only the ''ray'' path(s) from ''A'' to ''B'', but also an infinitude of near ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |