|
Dual Uniform Polyhedra
A dual uniform polyhedron is the dual polyhedron, dual of a uniform polyhedron. Where a uniform polyhedron is vertex-transitive, a dual uniform polyhedron is face-transitive. Enumeration The face-transitive polyhedra comprise a set of 9 regular polyhedra, two finite sets comprising 66 non-regular polyhedra, and two infinite sets: * 5 regular convex Platonic solids: regular tetrahedron, cube, regular octahedron, regular dodecahedron, and regular icosahedron. The regular octahedron is dual to the cube, and the regular icosahedron is dual to the regular dodecahedron. The regular tetrahedron is Self-dual polyhedron, self-dual, meaning its dual is the regular tetrahedron itself. * 4 regular star Kepler–Poinsot solids: great dodecahedron, small stellated dodecahedron, great icosahedron, and great stellated dodecahedron. The great dodecahedron is dual to the small stellated dodecahedron, and the great icosahedron is dual to the great stellated dodecahedron. * 13 convex Catalan soli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron. Duality preserves the symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solids and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron is self-dual. The dual of an isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the polyhedron) is an isohedral polyhedron (one in which any two faces are equivalent .., and vice ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Stellated Dodecahedron
In geometry, the great stellated dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol . It is one of four nonconvex regular polyhedra. It is composed of 12 intersecting pentagrammic faces, with three pentagrams meeting at each vertex. It shares its vertex arrangement, although not its vertex figure or vertex configuration, with the regular dodecahedron, as well as being a stellation of a (smaller) dodecahedron. It is the only dodecahedral stellation with this property, apart from the dodecahedron itself. Its dual, the great icosahedron, is related in a similar fashion to the icosahedron. Shaving the triangular pyramids off results in an icosahedron. If the pentagrammic faces are broken into triangles, it is topologically related to the triakis icosahedron, with the same face connectivity, but much taller isosceles In geometry, an isosceles triangle () is a triangle that has two sides of equal length and two angles of equal measure. Sometimes it is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Polyhedron
In geometry, a uniform polyhedron has regular polygons as Face (geometry), faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruence (geometry), congruent. Uniform polyhedra may be Regular polyhedron, regular (if also Isohedral figure, face- and Isotoxal figure, edge-transitive), Quasiregular polyhedron, quasi-regular (if also edge-transitive but not face-transitive), or Semiregular polyhedron, semi-regular (if neither edge- nor face-transitive). The faces and vertices don't need to be Convex polyhedron, convex, so many of the uniform polyhedra are also Star polyhedron, star polyhedra. There are two infinite classes of uniform polyhedra, together with 75 other polyhedra. They are 2 infinite classes of Prism (geometry), prisms and antiprisms, the convex polyhedrons as in 5 Platonic solids and 13 Archimedean solids—2 Quasiregular polyhedron, quasiregular and 11 Semiregular polyhedron, semiregular&m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intersphere
In geometry, the midsphere or intersphere of a convex polyhedron is a sphere which is tangent to every edge of the polyhedron. Not every polyhedron has a midsphere, but the uniform polyhedra, including the regular, quasiregular and semiregular polyhedra and their duals (Catalan solids) all have midspheres. The radius of the midsphere is called the midradius. A polyhedron that has a midsphere is said to be midscribed about this sphere. When a polyhedron has a midsphere, one can form two perpendicular circle packings on the midsphere, one corresponding to the adjacencies between vertices of the polyhedron, and the other corresponding in the same way to its polar polyhedron, which has the same midsphere. The length of each polyhedron edge is the sum of the distances from its two endpoints to their corresponding circles in this circle packing. Every convex polyhedron has a combinatorially equivalent polyhedron, the canonical polyhedron, that does have a midsphere, centered at th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off. Definitions Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines across the connected faces, joining adjacent points around the face. When done, these lines form a complete circuit, i.e. a polygon, around the vertex. This polygon is the vertex figure. More precise formal definitions can vary quite widely, according to circumstance. For example Coxeter (e.g. 1948, 1954) varies his definition as convenient for the current area of discussion. Most of the following definitions of a vertex figure apply equally well to infinite tessellation, tilings or, by extension, to Honeycomb (geometry), space-filling tessellation with polytope Cell (geometry), cells and other higher-dimensional polytopes. As a flat slice Make a slice through the corner of the polyhedron, cutting through all the edges conn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
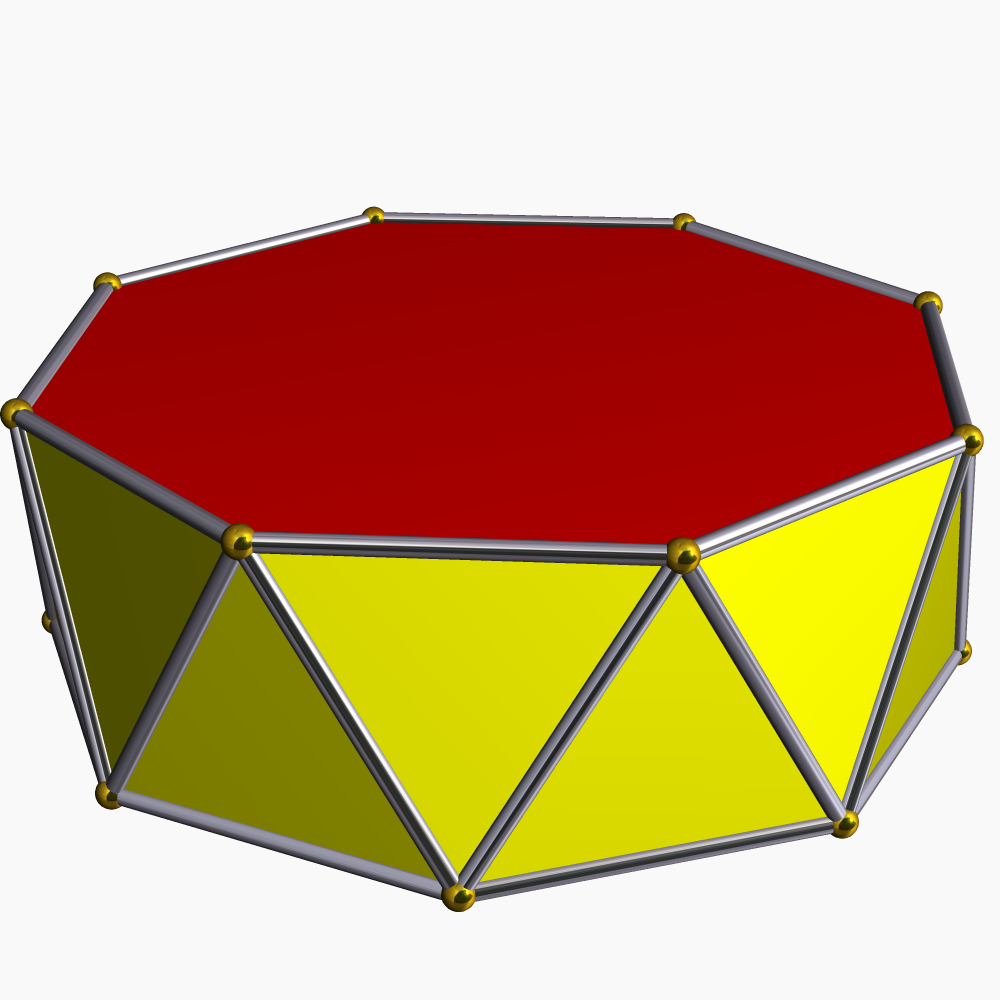
Antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway polyhedron notation, Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to Prism (geometry), prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History In his 1619 book ''Harmonices Mundi'', Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net (geometry), net of a hexagonal antiprism has been attributed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trapezohedra
In geometry, an trapezohedron, -trapezohedron, -antidipyramid, -antibipyramid, or -deltohedron Remarks: the faces of a deltohedron are deltoids; a (non-twisted) kite or deltoid can be dissected into two isosceles triangles or "deltas" (Δ), base-to-base. is the dual polyhedron of an antiprism. The faces of an are congruent and symmetrically staggered; they are called ''twisted kites''. With a higher symmetry, its faces are ''kites'' (sometimes also called ''trapezoids'', or ''deltoids''). The "" part of the name does not refer to faces here, but to two arrangements of each vertices around an axis of symmetry. The dual antiprism has two actual faces. An trapezohedron can be dissected into two equal pyramids and an antiprism. Terminology These figures, sometimes called deltohedra, are not to be confused with deltahedra, whose faces are equilateral triangles. ''Twisted'' ''trigonal'', ''tetragonal'', and ''hexagonal trapezohedra'' (with six, eight, and twelve ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prism (geometry)
In geometry, a prism is a polyhedron comprising an polygon Base (geometry), base, a second base which is a Translation (geometry), translated copy (rigidly moved without rotation) of the first, and other Face (geometry), faces, necessarily all parallelograms, joining corresponding sides of the two bases. All Cross section (geometry), cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids. Like many basic geometric terms, the word ''prism'' () was first used in Euclid's Elements, Euclid's ''Elements''. Euclid defined the term in Book XI as "a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms". However, this definition has been criticized for not being specific enough in regard to the nature of the bases (a cause of some confusion amongst generations of later geometry writers). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bipyramid
In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two Pyramid (geometry), pyramids together base (geometry), base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise specified the base Vertex (geometry), vertices are usually coplanar and a bipyramid is usually ''symmetric'', meaning the two pyramids are mirror images across their common base plane. When each apex (geometry), apex (, the off-base vertices) of the bipyramid is on a line perpendicular to the base and passing through its center, it is a ''right'' bipyramid; otherwise it is ''oblique''. When the base is a regular polygon, the bipyramid is also called ''regular''. Definition and properties A bipyramid is a polyhedron constructed by fusing two Pyramid (geometry), pyramids which share the same polygonal base (geometry), base; a pyramid is in turn constructed by connecting each vertex of its base to a single new vertex (geometry), vertex (th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Star Polyhedra
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both. The complete set of 57 nonprismatic uniform star polyhedra includes the 4 regular ones, called the Kepler–Poinsot polyhedra, 14 quasiregular ones, and 39 semiregular ones. There are also two infinite sets of ''uniform star prisms'' and ''uniform star antiprisms''. Just as (nondegenerate) star polygons (which have polygon density greater than 1) correspond to circular polygons with overlapping tiles, star polyhedra that do not pass through the center have polytope density greater than 1, and correspond to spherical polyhedra with overlapping tiles; there are 47 nonprismatic such uniform star polyhedra. The remaining 10 nonprismatic uniform star polyhedra, those that pass through the center, are the hemipolyhedra as well ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedean Solids
The Archimedean solids are a set of thirteen convex polyhedra whose faces are regular polygon and are vertex-transitive, although they aren't face-transitive. The solids were named after Archimedes, although he did not claim credit for them. They belong to the class of uniform polyhedra, the polyhedra with regular faces and symmetric vertices. Some Archimedean solids were portrayed in the works of artists and mathematicians during the Renaissance. The elongated square gyrobicupola or ' is an extra polyhedron with regular faces and congruent vertices, but it is not generally counted as an Archimedean solid because it is not vertex-transitive. The solids The Archimedean solids have a single vertex configuration and highly symmetric properties. A vertex configuration indicates which regular polygons meet at each vertex. For instance, the configuration 3 \cdot 5 \cdot 3 \cdot 5 indicates a polyhedron in which each vertex is met by alternating two triangles and two pentagons. Highl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |