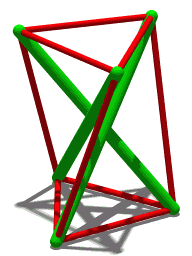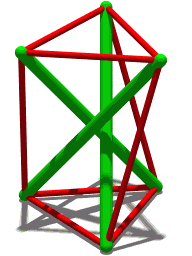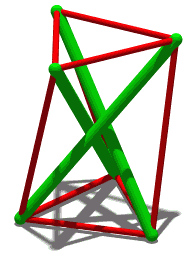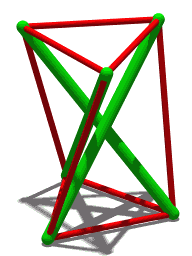
|
Császár Polyhedron
In geometry, the Császár polyhedron () is a nonconvex toroidal polyhedron with 14 triangular faces. This polyhedron has no diagonals; every pair of vertices is connected by an edge. The seven vertices and 21 edges of the Császár polyhedron form an embedding of the complete graph onto a topological torus. Of the 35 possible triangles from vertices of the polyhedron, only 14 are faces. Complete graph The tetrahedron and the Császár polyhedron are the only two known polyhedra (having a manifold boundary) without any diagonals: every two vertices of the polygon are connected by an edge, so there is no line segment between two vertices that does not lie on the polyhedron boundary. That is, the vertices and edges of the Császár polyhedron form a complete graph. The combinatorial description of this polyhedron has been described earlier by Möbius. Three additional different polyhedra of this type can be found in a paper by . If the boundary of a polyhedron with ''v'' ve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toroidal Polyhedron
In geometry, a toroidal polyhedron is a polyhedron which is also a toroid (a -holed torus), having a topology (Mathematics), topological Genus (mathematics), genus () of 1 or greater. Notable examples include the Császár polyhedron, Császár and Szilassi polyhedron, Szilassi polyhedra. Variations in definition Toroidal polyhedra are defined as collections of polygons that meet at their edges and vertices, forming a manifold as they do. That is, each edge should be shared by exactly two polygons, and at each vertex the edges and faces that meet at the vertex should be linked together in a single cycle of alternating edges and faces, the link (geometry), link of the vertex. For toroidal polyhedra, this manifold is an orientability, orientable surface. Some authors restrict the phrase "toroidal polyhedra" to mean more specifically polyhedra topologically equivalent to the (genus 1) torus. In this area, it is important to distinguish embedding, embedded toroidal polyhedra, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tetrahedron is the simplest of all the ordinary convex polytope, convex polyhedra. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean geometry, Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid (geometry), pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron, the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such net (polyhedron), nets. For any tetrahedron there exists a sphere (called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonconvex Polyhedra
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both. The complete set of 57 nonprismatic uniform star polyhedra includes the 4 regular ones, called the Kepler–Poinsot polyhedron, Kepler–Poinsot polyhedra, 14 Quasiregular polyhedron#Nonconvex examples, quasiregular ones, and 39 semiregular ones. There are also two infinite sets of Uniform_polyhedron#.28p_2_2.29_Prismatic_.5Bp.2C2.5D.2C_I2.28p.29_family_.28Dph_dihedral_symmetry.29, ''uniform star prisms'' and ''uniform star antiprisms''. Just as (nondegenerate) star polygons (which have density (polytope), polygon density greater than 1) correspond to circular polygons with overlapping Tessellation, tiles, star polyhedra that do not pass through the center have polytope density greater than 1, and correspond to spherical polyhe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schönhardt Polyhedron
In geometry, a Schönhardt polyhedron is a polyhedron with the same combinatorial structure as a regular octahedron, but with dihedral angles that are non-convex along three disjoint edges. Because it has no interior diagonals, it cannot be triangulated into tetrahedra without adding new vertices. It has the fewest vertices of any polyhedron that cannot be triangulated. It is named after the German mathematician Erich Schönhardt, who described it in 1928, although the artist Karlis Johansons had exhibited a related structure in 1921. One construction for the Schönhardt polyhedron starts with a triangular prism and twists the two equilateral triangle faces of the prism relative to each other, breaking each square face into two triangles separated by a non-convex edge. Some twist angles produce a ''jumping polyhedron'' whose two solid forms share the same face shapes. A 30° twist instead produces a ''shaky polyhedron'', rigid but not infinitesimally rigid, whose edges fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagon
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°. Regular hexagon A regular hexagon is defined as a hexagon that is both equilateral and equiangular. In other words, a hexagon is said to be regular if the edges are all equal in length, and each of its internal angle is equal to 120°. The Schläfli symbol denotes this polygon as \ . However, the regular hexagon can also be considered as the cutting off the vertices of an equilateral triangle, which can also be denoted as \mathrm\ . A regular hexagon is bicentric, meaning that it is both cyclic (has a circumscribed circle) and tangential (has an inscribed circle). The common length of the sides equals the radius of the circumscribed circle or circumcircle, which equals \tfrac times the apothem (radius of the inscribed circle). Measurement The longest diagonals of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lajos Szilassi
Lajos Szilassi (born in 1942 in Szentes, Hungary) was a professor of mathematics at the University of Szeged who worked in projective geometry, projective and non-Euclidean geometry, applying his research to computer generated solutions to geometric problems.Lajos Szilassi is 70 Department of Geometry, Bolyai Institute, Faculty of Science, University of Szeged Biography Szilassi obtained his undergraduate degree in 1966 at the Bolyai Institute of the József Attila University, majoring in mathematical representation geometry. He taught for six years in a secondary school before joining the Department of Mathematics at Gyula Juhász Teacher Training College. In 1981, he received a bachelor's associate degree. He then received his Doctor rerum naturalium, ''Doctor rerum naturalium'' d ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
