|
Consumer-resource Model
In theoretical ecology and nonlinear dynamics, consumer-resource models (CRMs) are a class of ecological models in which a community of consumer species compete for a common pool of resources. Instead of species interacting directly, all species-species interactions are mediated through resource dynamics. Consumer-resource models have served as fundamental tools in the quantitative development of theories of niche construction, coexistence, and biological diversity. These models can be interpreted as a quantitative description of a single trophic level. A general consumer-resource model consists of ' resources whose abundances are R_1,\dots,R_M and ' consumer species whose populations are N_1,\dots,N_S. A general consumer-resource model is described by the system of coupled ordinary differential equations, \begin \frac &= N_i g_i(R_1,\dots,R_M), &&\qquad i =1 ,\dots,S, \\ \frac &= f_\alpha(R_1,\dots,R_M,N_1,\dots,N_S), &&\qquad \alpha = 1,\dots,M \end where g_i, depending only o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Ecology
Theoretical ecology is the scientific discipline devoted to the study of ecosystem, ecological systems using theoretical methods such as simple conceptual models, mathematical models, computer simulation, computational simulations, and advanced data analysis. Effective models improve understanding of the natural world by revealing how the dynamics of species populations are often based on fundamental biological conditions and processes. Further, the field aims to unify a diverse range of empirical observations by assuming that common, mechanistic processes generate observable phenomena across species and ecological environments. Based on biologically realistic assumptions, theoretical ecologists are able to uncover novel, non-intuitive insights about natural processes. Theoretical results are often verified by empirical and observational studies, revealing the power of theoretical methods in both predicting and understanding the noisy, diverse biological world. The field is broad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constrained Optimization Problem
In mathematical optimization, constrained optimization (in some contexts called constraint optimization) is the process of optimizing an objective function with respect to some variables in the presence of constraints on those variables. The objective function is either a cost function or energy function, which is to be minimized, or a reward function or utility function, which is to be maximized. Constraints can be either hard constraints, which set conditions for the variables that are required to be satisfied, or soft constraints, which have some variable values that are penalized in the objective function if, and based on the extent that, the conditions on the variables are not satisfied. Relation to constraint-satisfaction problems The constrained-optimization problem (COP) is a significant generalization of the classic constraint-satisfaction problem (CSP) model. COP is a CSP that includes an ''objective function'' to be optimized. Many algorithms are used to handle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
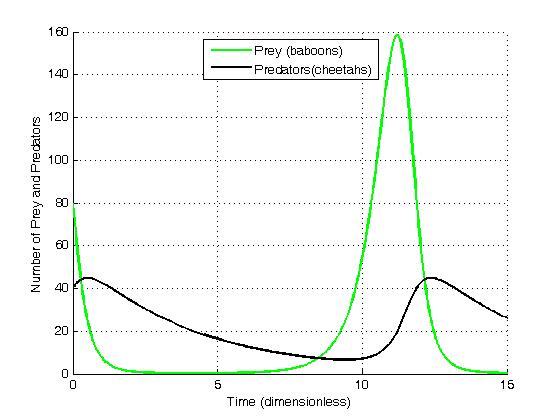
Competitive Lotka–Volterra Equations
The competitive Lotka–Volterra equations are a simple model of the population dynamics of species competing for some common resource. They can be further generalised to the generalized Lotka–Volterra equation to include trophic interactions. Overview The form is similar to the Lotka–Volterra equations for predation in that the equation for each species has one term for self-interaction and one term for the interaction with other species. In the equations for predation, the base population model is exponential. For the competition equations, the logistic equation is the basis. The logistic population model, when used by ecologists often takes the following form: = rx\left(1-\right). Here is the size of the population at a given time, is inherent per-capita growth rate, and is the carrying capacity. Two species Given two populations, and , with logistic dynamics, the Lotka–Volterra formulation adds an additional term to account for the species' interactions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Competition (biology)
Competition is an Biological interaction, interaction between organisms or species in which both require one or more Resource (biological), resources that are in Limiting factor, limited supply (such as food, water, or Territory (animal), territory). Competition lowers the Fitness (biology), fitness of both organisms involved since the presence of one of the organisms always reduces the amount of the resource available to the other. In the study of community ecology, competition within and between members of a species is an important biological interaction. Competition is one of many interacting Biotic component, biotic and Abiotic component, abiotic factors that affect Community (ecology), community structure, species diversity, and population dynamics (shifts in a population over time). There are three major Mechanism (biology), mechanisms of competition: interference, exploitation, and apparent competition (in order from most direct to least direct). Interference and exploitat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Ecology
Theoretical ecology is the scientific discipline devoted to the study of ecosystem, ecological systems using theoretical methods such as simple conceptual models, mathematical models, computer simulation, computational simulations, and advanced data analysis. Effective models improve understanding of the natural world by revealing how the dynamics of species populations are often based on fundamental biological conditions and processes. Further, the field aims to unify a diverse range of empirical observations by assuming that common, mechanistic processes generate observable phenomena across species and ecological environments. Based on biologically realistic assumptions, theoretical ecologists are able to uncover novel, non-intuitive insights about natural processes. Theoretical results are often verified by empirical and observational studies, revealing the power of theoretical methods in both predicting and understanding the noisy, diverse biological world. The field is broad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
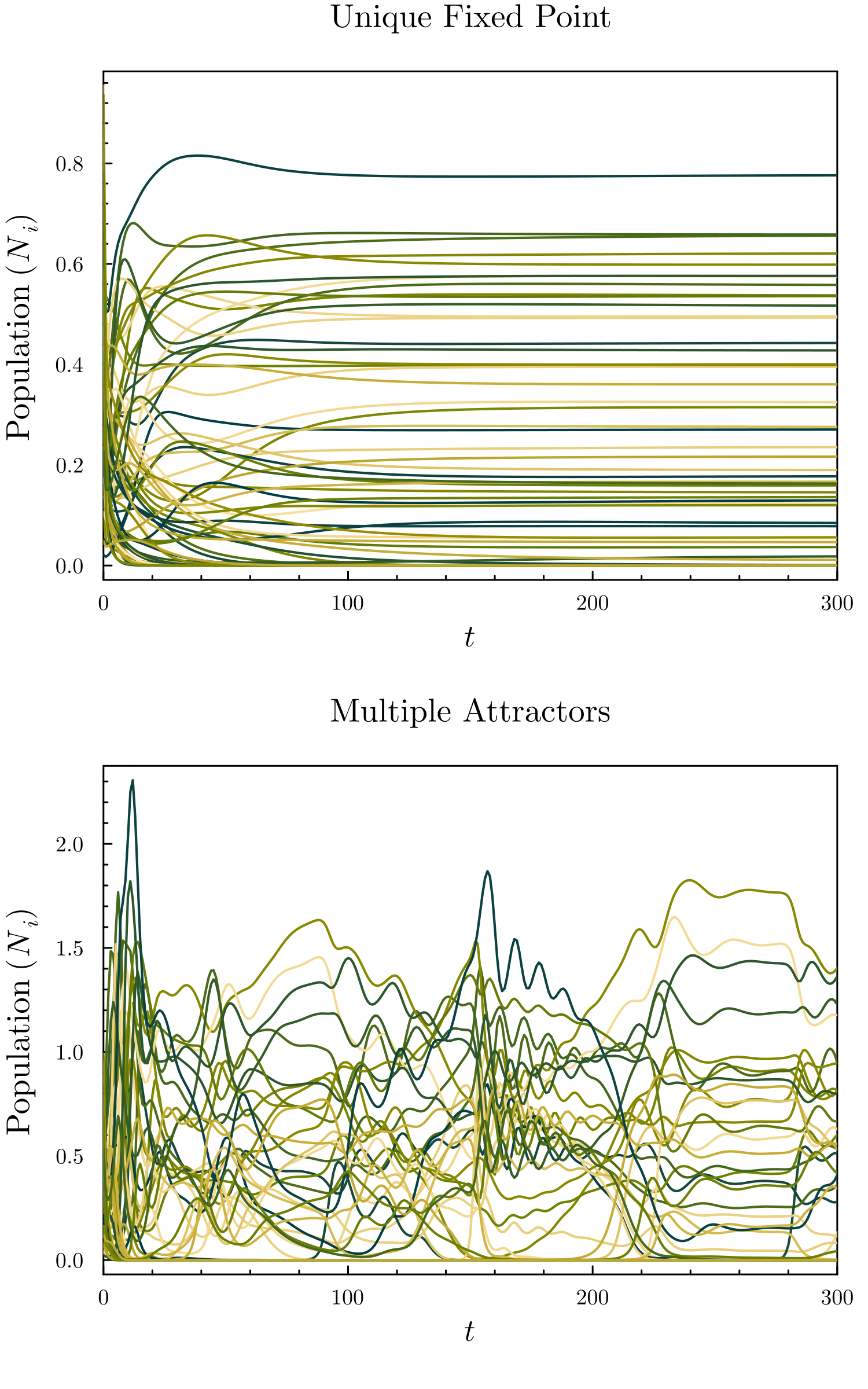
Random Generalized Lotka–Volterra Model
The random generalized Lotka–Volterra model (rGLV) is an ecological model and Random dynamical system, random set of coupled ordinary differential equations where the parameters of the generalized Lotka–Volterra equation are sampled from a probability distribution, analogously to quenched disorder. The rGLV models dynamics of a community of species in which each species' abundance grows towards a carrying capacity but is depleted due to Competition (biology), competition from the presence of other species. It is often analyzed in the Thermodynamic limit, many-species limit using tools from statistical physics, in particular from spin glass theory. The rGLV has been used as a tool to analyze Emergence, emergent macroscopic behavior in microbial communities with dense, strong interspecies interactions. The model has served as a context for theoretical investigations studying Diversity (ecology), diversity-Stability (ecology), stability relations in community ecology and proper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Normal
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is f(x) = \frac e^\,. The parameter is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma^2 is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution conver ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cavity Method
The cavity method is a mathematical method presented by Marc Mézard, Giorgio Parisi and Miguel Angel Virasoro in 1987 to derive and solve some mean field-type models in statistical physics, specially adapted to disordered systems. The method has been used to compute properties of ground states in many condensed matter and optimization problems. Initially invented to deal with the Sherrington–Kirkpatrick model of spin glasses, the cavity method has shown wider applicability. It can be regarded as a generalization of the Bethe– Peierls iterative method in tree-like graphs, to the case of a graph with loops that are not too short. The cavity method can solve many problems also solvable using the replica trick but has the advantage of being more intuitive and less mathematically subtle than replica-based methods. The cavity method proceeds by perturbing a large system with the addition of a non-thermodynamic number of additional constituents and approximating the response of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean-field Theory
In physics and probability theory, Mean-field theory (MFT) or Self-consistent field theory studies the behavior of high-dimensional random (stochastic) models by studying a simpler model that approximates the original by averaging over Degrees of freedom (statistics), degrees of freedom (the number of values in the final calculation of a statistic that are free to vary). Such models consider many individual components that interact with each other. The main idea of MFT is to replace all fundamental interaction, interactions to any one body with an average or effective interaction, sometimes called a ''molecular field''. This reduces any many-body problem into an effective one-body problem. The ease of solving MFT problems means that some insight into the behavior of the system can be obtained at a lower computational cost. MFT has since been applied to a wide range of fields outside of physics, including statistical inference, graphical models, neuroscience, artificial intelligenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Cone
In linear algebra, a cone—sometimes called a linear cone to distinguish it from other sorts of cones—is a subset of a real vector space that is closed under positive scalar multiplication; that is, C is a cone if x\in C implies sx\in C for every . This is a broad generalization of the standard cone in Euclidean space. A convex cone is a cone that is also closed under addition, or, equivalently, a subset of a vector space that is closed under linear combinations with positive coefficients. It follows that convex cones are convex sets. The definition of a convex cone makes sense in a vector space over any ordered field, although the field of real numbers is used most often. Definition A subset C of a vector space is a cone if x\in C implies sx\in C for every s>0. Here s>0 refers to (strict) positivity in the scalar field. Competing definitions Some other authors require ,\infty)C\subset C or even 0\in C. Some require a cone to be convex and/or satisfy C\cap-C\subset\. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isocline
300px, Fig. 1: Isoclines (blue), slope field (black), and some solution curves (red) of ''y = ''xy''. The solution curves are y = C e^. Given a family of curves, assumed to be differentiable, an isocline for that family is formed by the set of points at which some member of the family attains a given slope. The word comes from the Greek words ἴσος (isos), meaning "same", and the κλίνειν (klenein), meaning "make to slope". Generally, an isocline will itself have the shape of a curve or the union of a small number of curves. Isoclines are often used as a graphical method of solving ordinary differential equations In mathematics, an ordinary differential equation (ODE) is a differential equation (DE) dependent on only a single independent variable. As with any other DE, its unknown(s) consists of one (or more) function(s) and involves the derivatives .... In an equation of the form ''y' = f''(''x'', ''y''), the isoclines are lines in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |