|
Condorcet Method
A Condorcet method (; ) is an election method that elects the candidate who wins a majority of the vote in every head-to-head election against each of the other candidates, whenever there is such a candidate. A candidate with this property, the ''pairwise champion'' or ''beats-all winner'', is formally called the ''Condorcet winner'' or ''Pairwise Majority Rule Winner'' (PMRW). The head-to-head elections need not be done separately; a voter's choice within any given pair can be determined from the ranking. Some elections may not yield a Condorcet winner because voter preferences may be cyclic—that is, it is possible that every candidate has an opponent that defeats them in a two-candidate contest. The possibility of such cyclic preferences is known as the Condorcet paradox. However, a smallest group of candidates that beat all candidates not in the group, known as the Smith set, always exists. The Smith set is guaranteed to have the Condorcet winner in it should one exist. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Preferential Ballot
Ranked voting is any voting system that uses voters' Ordinal utility, rankings of candidates to choose a single winner or multiple winners. More formally, a ranked vote system depends only on voters' total order, order of preference of the candidates. Ranked voting systems vary dramatically in how preferences are tabulated and counted, which gives them Comparison of voting rules, very different properties. In instant-runoff voting (IRV) and the single transferable vote system (STV), lower preferences are used as contingencies (back-up preferences) and are only applied when all higher-ranked preferences on a ballot have been eliminated or when the vote has been cast for a candidate who has been elected and surplus votes need to be transferred. Ranked votes of this type do not suffer the problem that a marked lower preference may be used against a voter's higher marked preference. Some ranked vote systems use ranks as weights; these systems are called positional voting. In the B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
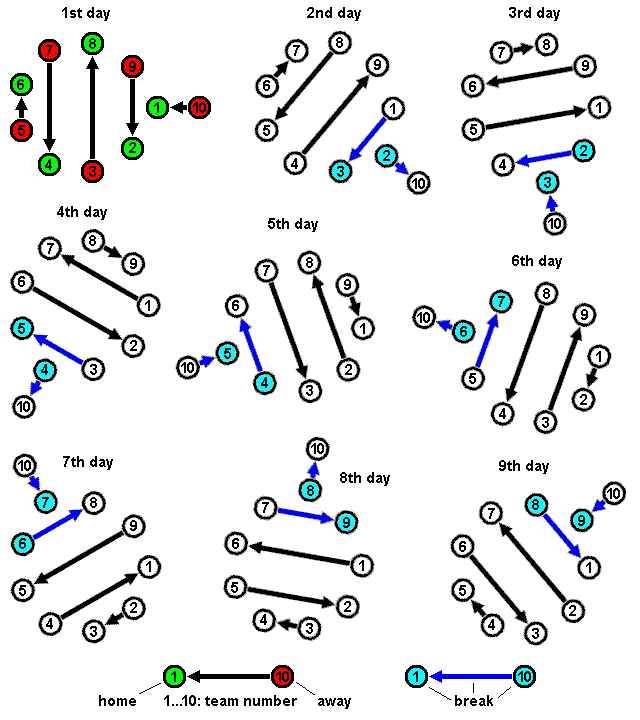
Round-robin Tournament
A round-robin tournament or all-play-all tournament is a competition format in which each contestant meets every other participant, usually in turn.''Webster's Third New International Dictionary of the English Language, Unabridged'' (1971, G. & C. Merriam Co), p.1980. A round-robin contrasts with an elimination tournament, wherein participants are eliminated after a certain number of wins or losses. Terminology The term ''round-robin'' is derived from the French term ('ribbon'). Over time, the term became idiomized to ''robin''. In a ''single round-robin'' schedule, each participant plays every other participant once. If each participant plays all others twice, this is frequently called a ''double round-robin''. The term is rarely used when all participants play one another more than twice, and is never used when one participant plays others an unequal number of times, as is the case in almost all of the major North American professional sports leagues. In the United Kingdom, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Majority Loser Criterion
The majority loser criterion is a criterion to evaluate single-winner voting systems. The criterion states that if a majority of voters give a candidate no support, i.e. do not list that candidate on their ballot, that candidate must lose (unless no candidate is accepted by a majority of voters). Either of the Condorcet loser criterion or the mutual majority criterion implies the majority loser criterion. However, the Condorcet criterion does not imply the majority loser criterion, since the minimax method satisfies the Condorcet but not the majority loser criterion. Also, the majority criterion is logically independent from the majority loser criterion, since the plurality rule satisfies the majority but not the majority loser criterion, and the anti-plurality rule satisfies the majority loser but not the majority criterion. There is no positional scoring rule which satisfies both the majority and the majority loser criterion, but several non-positional rules, including ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutual Majority Criterion
The mutual majority criterion is a criterion for evaluating electoral systems. It is also known as the majority criterion for solid coalitions and the generalized majority criterion. This criterion requires that whenever a majority of voters prefer a group of candidates above all others, then the winner must be a candidate from that group. The mutual majority criterion may also be thought of as the single-winner case of Droop- Proportionality for Solid Coalitions. Formal definition Let L be a subset of candidates. A solid coalition in support of L is a group of voters who strictly prefer all members of L to all candidates outside of L. In other words, each member of the solid coalition ranks their least-favorite member of L higher than their favorite member outside L. Note that the members of the solid coalition may rank the members of L differently. The mutual majority criterion says that if there is a solid coalition of voters in support of L, and this solid coalition consist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plurality (voting)
A plurality vote (in North American English) or relative majority (in British English) describes the circumstance when a party, candidate, or proposition polls more votes than any other but does not receive more than half of all votes cast. For example, if from 100 votes that were cast, 45 were for ''candidate A'', 30 were for ''candidate B'' and 25 were for ''candidate C'', then ''candidate A'' received a plurality of votes but not a majority. In some election contests, the winning candidate or proposition may need only a plurality, depending on the rules of the organization holding the vote. Versus majority In international institutional law, a ''simple majority'' (also a ''plurality'') is the largest number of votes cast (disregarding abstentions) ''among'' alternatives, always true when only two are in the competition. In some circles, a majority means more than half of the total including abstentions. However, in many jurisdictions, a simple majority is defined as more vo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
First-past-the-post
First-past-the-post (FPTP)—also called choose-one, first-preference plurality (FPP), or simply plurality—is a single-winner voting rule. Voters mark one candidate as their favorite, or First-preference votes, first-preference, and the candidate with more first-preference votes than any other candidate (a Plurality (voting), ''plurality'') is elected, even if they do not have more than half of votes (a ''majority''). FPP has been used to elect part of the House of Commons of the United Kingdom, British House of Commons since the Middle Ages before spreading throughout the British Empire. Throughout the 20th century, many countries that previously used FPP have abandoned it in favor of other electoral systems, including the former British colonies of Australia and New Zealand. FPP is still De jure, officially used in the majority of U.S. state, US states for most elections. However, the combination of Partisan primary, partisan primaries and a two-party system in these jurisd ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Addition
In mathematics, matrix addition is the operation of adding two matrices by adding the corresponding entries together. For a vector, \vec\!, adding two matrices would have the geometric effect of applying each matrix transformation separately onto \vec\!, then adding the transformed vectors. :\mathbf\vec + \mathbf\vec = (\mathbf + \mathbf)\vec\! Definition Two matrices must have an equal number of rows and columns to be added. In which case, the sum of two matrices A and B will be a matrix which has the same number of rows and columns as A and B. The sum of A and B, denoted , is computed by adding corresponding elements of A and B: :\begin \mathbf+\mathbf & = \begin a_ & a_ & \cdots & a_ \\ a_ & a_ & \cdots & a_ \\ \vdots & \vdots & \ddots & \vdots \\ a_ & a_ & \cdots & a_ \\ \end + \begin b_ & b_ & \cdots & b_ \\ b_ & b_ & \cdots & b_ \\ \vdots & \vdots & \ddots & \vdots \\ b_ & b_ & \cdots & b_ \\ \end \\ & = \begin a_ + b_ & a_ + b_ & \cdots & a_ + b_ \\ a_ + b_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (: matrices) is a rectangle, rectangular array or table of numbers, symbol (formal), symbols, or expression (mathematics), expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a " matrix", or a matrix of dimension . Matrices are commonly used in linear algebra, where they represent linear maps. In geometry, matrices are widely used for specifying and representing geometric transformations (for example rotation (mathematics), rotations) and coordinate changes. In numerical analysis, many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions. Matrices are used in most areas of mathematics and scientific fields, either directly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independence Of Smith-dominated Alternatives
Independence of Smith-dominated alternatives (ISDA, also known as Smith- IIA) is a voting system criterion which says that the winner of an election should not be affected by candidates who are not in the Smith set. Another way of defining ISDA is to say that adding a new candidate should not change the winner of an election, ''unless'' that new candidate would beat the original winner, either directly or indirectly. Complying methods Schulze and Ranked Pairs are independent of Smith-dominated alternatives. Any voting system can be forced to satisfy ISDA by first eliminating all candidates outside the Smith set, then running the full algorithm. Ambiguity Smith- IIA can sometimes be taken to mean independence of non-Smith ''irrelevant'' alternatives, i.e. that no ''losing'' candidate outside the Smith set can affect the result. This differs slightly from the above definition, in that methods passing independence of irrelevant alternatives (but not the Smith criterion) also sa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Write-in Candidate
A write-in candidate is a candidate whose name does not appear on the ballot but seeks election by asking voters to cast a vote for the candidate by physically writing in the person's name on the ballot. Depending on electoral law it may be possible to win an election by winning a sufficient number of such write-in votes, which count equally as if the person were formally listed on the ballot. Writing in a name that is not already on the election ballot is a permitted practice in the United States. However, some other jurisdictions have allowed this practice. In the United States, there are variations in laws governing write-in candidates, depending on the office (federal or local) and whether the election is a primary election or the general election; general practice is an empty field close by annotated to explain its purpose on the ballot if it applies. In five U.S. states there are no elections to which it can apply, under their present laws. Election laws are enacted by each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Score Voting
Score voting, sometimes called range voting, is an electoral system for single-seat elections. Voters give each candidate a numerical score, and the candidate with the highest average score is elected. Score voting includes the well-known approval voting (used to calculate approval ratings), but also lets voters give partial (in-between) approval ratings to candidates. Usage Political use Historical A crude form of score voting was used in some elections in ancient Sparta, by measuring how loudly the crowd shouted for different candidates. This has a modern-day analog of using clapometers in some television shows and the judging processes of some athletic competitions. Beginning in the 13th century, the Republic of Venice elected the Doge of Venice using a multi-stage process with multiple rounds of score voting. This may have contributed to the Republic's longevity, being partly responsible for its status as the longest-lived democracy in world history. Score voting w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Borda Count
The Borda method or order of merit is a positional voting rule that gives each candidate a number of points equal to the number of candidates ranked below them: the lowest-ranked candidate gets 0 points, the second-lowest gets 1 point, and so on. The candidate with the most points wins. The Borda count has been independently reinvented several times, with the first recorded proposal in 1435 being by Nicholas of Cusa (see History below), but is named after the 18th-century French mathematician and naval engineer Jean-Charles de Borda, who re-devised the system in 1770. The Borda count is well-known in social choice theory both for its pleasant theoretical properties and its ease of manipulation. In the absence of strategic voting and strategic nomination, the Borda count tends to elect broadly-acceptable options or candidates (rather than consistently following the preferences of a majority); when both voting and nomination patterns are completely random, the Borda count gener ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |