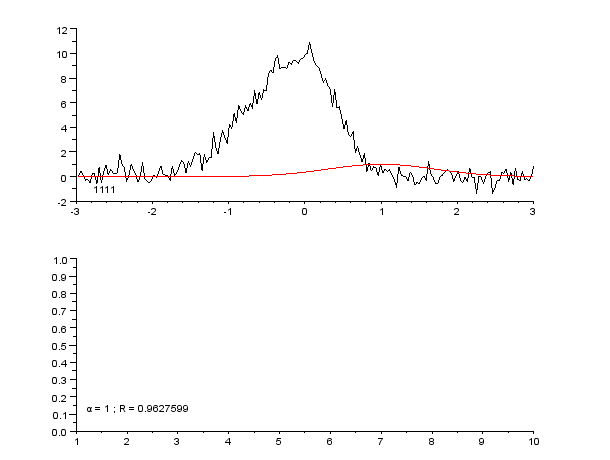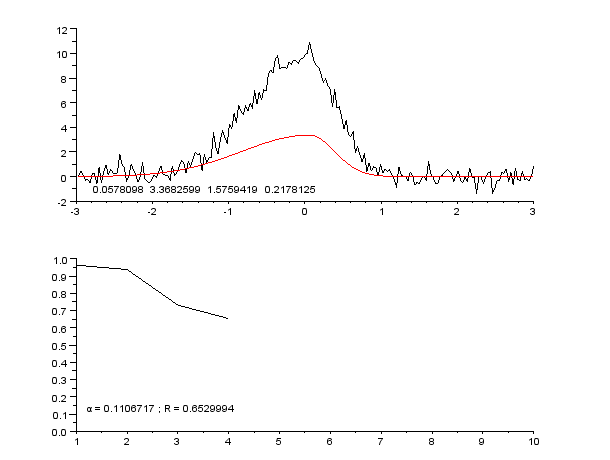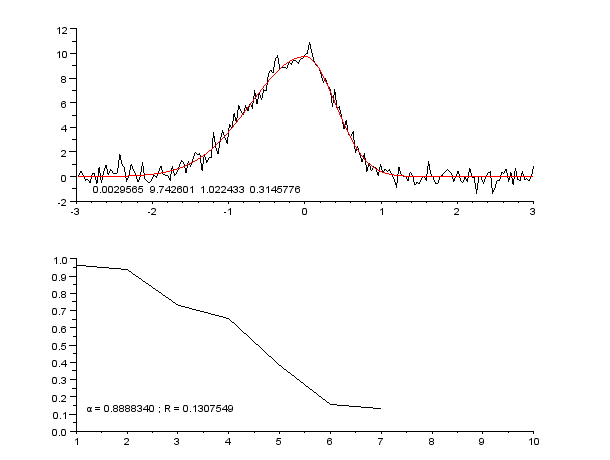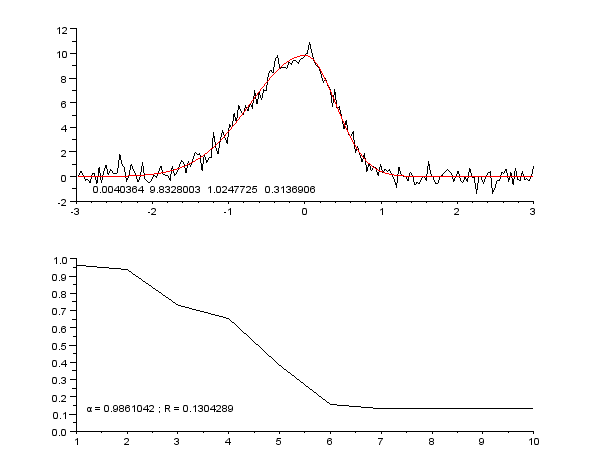
|
Colebrook–White Equation
In fluid dynamics, the Darcy friction factor formulae are equations that allow the calculation of the ''Darcy friction factor'', a dimensionless quantity used in the Darcy–Weisbach equation, for the description of friction losses in pipe flow as well as open-channel flow. The Darcy friction factor is also known as the ''Darcy–Weisbach friction factor'', ''resistance coefficient'' or simply ''friction factor''; by definition it is four times larger than the Fanning friction factor. Notation In this article, the following conventions and definitions are to be understood: * The Reynolds number Re is taken to be Re = ''V'' ''D'' / ν, where ''V'' is the mean velocity of fluid flow, ''D'' is the pipe diameter, and where ν is the kinematic viscosity μ / ρ, with μ the fluid's Dynamic viscosity, and ρ the fluid's density. * The pipe's relative roughness ε / ''D'', where ε is the pipe's effective roughness height and ''D'' the pipe (inside) diameter. * ''f'' stands for the D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion) and (the study of water and other liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moment (physics), moments on aircraft, determining the mass flow rate of petroleum through pipeline transport, pipelines, weather forecasting, predicting weather patterns, understanding nebulae in interstellar space, understanding large scale Geophysical fluid dynamics, geophysical flows involving oceans/atmosphere and Nuclear weapon design, modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydraulic Radius
The Manning formula or Manning's equation is an empirical formula estimating the average velocity of a liquid in an open channel flow (flowing in a conduit that does not completely enclose the liquid). However, this equation is also used for calculation of flow variables in case of flow in partially full conduits, as they also possess a free surface like that of open channel flow. All flow in so-called open channels is driven by gravity. It was first presented by the French engineer in 1867, and later re-developed by the Irish engineer Robert Manning in 1890. Thus, the formula is also known in Europe as the Gauckler–Manning formula or Gauckler–Manning–Strickler formula (after Albert Strickler). The Gauckler–Manning formula is used to estimate the average velocity of water flowing in an open channel in locations where it is not practical to construct a weir or flume to measure flow with greater accuracy. Manning's equation is also commonly used as part of a numeric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equations Of Fluid Dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion) and (the study of water and other liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moment (physics), moments on aircraft, determining the mass flow rate of petroleum through pipeline transport, pipelines, weather forecasting, predicting weather patterns, understanding nebulae in interstellar space, understanding large scale Geophysical fluid dynamics, geophysical flows involving oceans/atmosphere and Nuclear weapon design, modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Colebrook Equation
In fluid dynamics, the Darcy friction factor formulae are equations that allow the calculation of the ''Darcy friction factor'', a dimensionless quantity used in the Darcy–Weisbach equation, for the description of friction losses in pipe flow as well as open-channel flow. The Darcy friction factor is also known as the ''Darcy–Weisbach friction factor'', ''resistance coefficient'' or simply ''friction factor''; by definition it is four times larger than the Fanning friction factor. Notation In this article, the following conventions and definitions are to be understood: * The Reynolds number Re is taken to be Re = ''V'' ''D'' / ν, where ''V'' is the mean velocity of fluid flow, ''D'' is the pipe diameter, and where ν is the kinematic viscosity μ / ρ, with μ the fluid's Dynamic viscosity, and ρ the fluid's density. * The pipe's relative roughness ε / ''D'', where ε is the pipe's effective roughness height and ''D'' the pipe (inside) diameter. * ''f'' stands for the D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hagen–Poiseuille Equation
In fluid dynamics, the Hagen–Poiseuille equation, also known as the Hagen–Poiseuille law, Poiseuille law or Poiseuille equation, is a physical law that gives the pressure drop in an incompressible and Newtonian fluid in laminar flow flowing through a long cylindrical pipe of constant cross section. It can be successfully applied to air flow in lung alveoli, or the flow through a drinking straw or through a hypodermic needle. It was experimentally derived independently by Jean Léonard Marie Poiseuille in 1838 and Gotthilf Heinrich Ludwig Hagen, and published by Hagen in 1839 and then by Poiseuille in 1840–41 and 1846. The theoretical justification of the Poiseuille law was given by George Stokes in 1845. The assumptions of the equation are that the fluid is incompressible and Newtonian; the flow is laminar through a pipe of constant circular cross-section that is substantially longer than its diameter; and there is no acceleration of fluid in the pipe. For velocities a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Law
In statistics, a power law is a Function (mathematics), functional relationship between two quantities, where a Relative change and difference, relative change in one quantity results in a relative change in the other quantity proportional to the change raised to a constant exponent: one quantity varies as a power of another. The change is independent of the initial size of those quantities. For instance, the area of a square has a power law relationship with the length of its side, since if the length is doubled, the area is multiplied by 2, while if the length is tripled, the area is multiplied by 3, and so on. Empirical examples The distributions of a wide variety of physical, biological, and human-made phenomena approximately follow a power law over a wide range of magnitudes: these include the sizes of craters on the moon and of solar flares, cloud sizes, the foraging pattern of various species, the sizes of activity patterns of neuronal populations, the frequencies of words ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Johann Nikuradse
Johann Nikuradse ( ka, ივანე ნიკურაძე, ''Ivane Nikuradze'') (November 20, 1894 – July 18, 1979) was a Georgia-born German engineer and physicist. His brother, Alexander Nikuradse, was also a Germany-based physicist and geopolitician known for his ties with Alfred Rosenberg and for his role in saving many Georgians during World War II. He was born in Samtredia, Georgia (then part of the Kutais Governorate, Imperial Russia) and studied at Kutaisi. In 1919, through the recommendations of the conspicuous Georgian scholar Petre Melikishvili, he went abroad for further studies. The 1921 Sovietization of Georgia precluded his return to homeland and Nikuradse naturalized as a German citizen. As PhD student of Ludwig Prandtl in 1920, he later worked as a researcher at the Kaiser Wilhelm Institute for Flow Research (now the Max Planck Institute for Dynamics and Self-Organization). He succeeded in putting himself in Prandtl's favour and thus advanced to the posi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paul Richard Heinrich Blasius
Paul Richard Heinrich Blasius (9 August 1883 – 24 April 1970) was a German fluid dynamics physicist. He was one of the first students of Prandtl Ludwig Prandtl (4 February 1875 – 15 August 1953) was a German Fluid mechanics, fluid dynamicist, physicist and aerospace scientist. He was a pioneer in the development of rigorous systematic mathematical analyses which he used for underlyin .... Blasius provided a mathematical basis for boundary-layer drag but also showed as early as 1911 that the resistance to flow through smooth pipes could be expressed in terms of the Reynolds number for both laminar and turbulent flow. After six years in science he changed to ''Ingenieurschule Hamburg'' (today: University of Applied Sciences Hamburg) and became a Professor. On 1 April 1962 Heinrich Blasius celebrated his 50th anniversary in teaching. He was active in his field until he died on 24 April 1970. One of his most notable contributions involves a description of the steady two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steffensen's Method
In numerical analysis, Steffensen's method is an iterative method for numerical root-finding named after Johan Frederik Steffensen that is similar to the secant method and to Newton's method. Steffensen's method achieves a quadratic order of convergence without using derivatives, whereas the more familiar Newton's method also converges quadratically, but requires derivatives and the secant method does not require derivatives but also converges less quickly than quadratically. Steffensen's method has the drawback that it requires two function evaluations per step, whereas the secant method requires only one evaluation per step, so it is not necessarily most efficient in terms of computational cost, depending on the number of iterations each requires. Newton's method also requires evaluating two functions per step – for the function and for its derivative – and its computational cost varies between being the same as Steffensen's method (for most functions, where calculation of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norwegian University Of Science And Technology
The Norwegian University of Science and Technology (NTNU; ) is a public university, public research university in Norway and the largest in terms of enrollment. The university's headquarters is located in Trondheim (city), Trondheim, with regional campuses in Gjøvik (town), Gjøvik and Ålesund (town), Ålesund. NTNU was inaugurated by the King-in-Council in 1996 as a result of the merger of the former University of Trondheim and other university-level institutions, with roots dating back to 1760. Later, some former university colleges were also incorporated. Depending on the ranking publication, the university typically ranks within a range of 101 and 400 globally. As of November 2022, the university boasts an approximate 9,000 employees and 42,000 students. NTNU has the main national responsibility for education and research in engineering and technology. This is likely attributable to the fact that it is the successor of Norway's pre-eminent engineering university, the Norwe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curve Fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function is constructed that approximately fits the data. A related topic is regression analysis, which focuses more on questions of statistical inference such as how much uncertainty is present in a curve that is fitted to data observed with random errors. Fitted curves can be used as an aid for data visualization, to infer values of a function where no data are available, and to summarize the relationships among two or more variables. Extrapolation refers to the use of a fitted curve beyond the range of the observed data, and is subject to a degree of uncertainty since it may reflect the method used to construct the curve as much as it reflects the observed data. For linear-algebraic ana ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert W Function
In mathematics, the Lambert function, also called the omega function or product logarithm, is a multivalued function, namely the Branch point, branches of the converse relation of the function , where is any complex number and is the exponential function. The function is named after Johann Heinrich Lambert, Johann Lambert, who considered a related problem in 1758. Building on Lambert's work, Leonhard Euler described the function per se in 1783. For each integer there is one branch, denoted by , which is a complex-valued function of one complex argument. is known as the principal branch. These functions have the following property: if and are any complex numbers, then : w e^ = z holds if and only if : w=W_k(z) \ \ \text k. When dealing with real numbers only, the two branches and suffice: for real numbers and the equation : y e^ = x can be solved for only if ; yields if and the two values and if . The Lambert function's branches cannot be expressed in terms o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |