|
Centered Trochoid
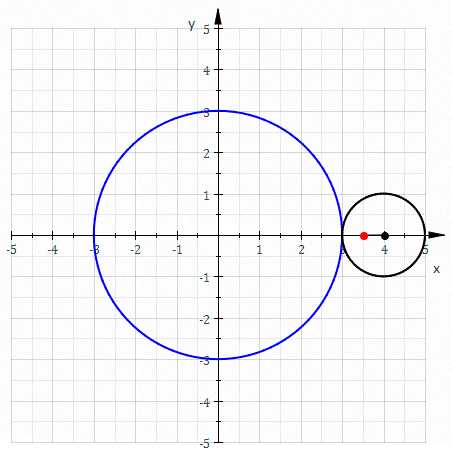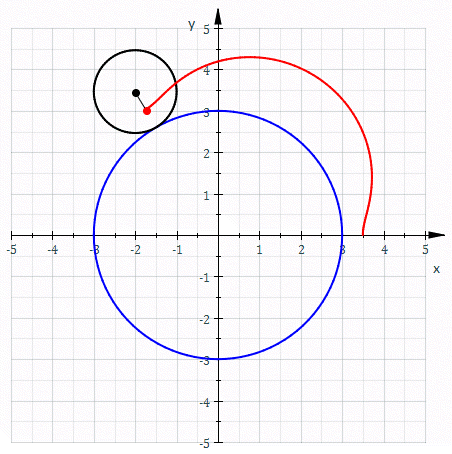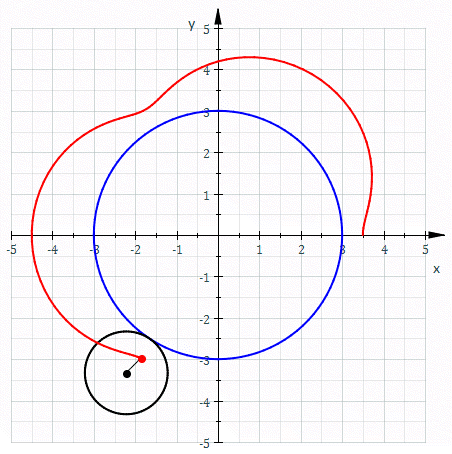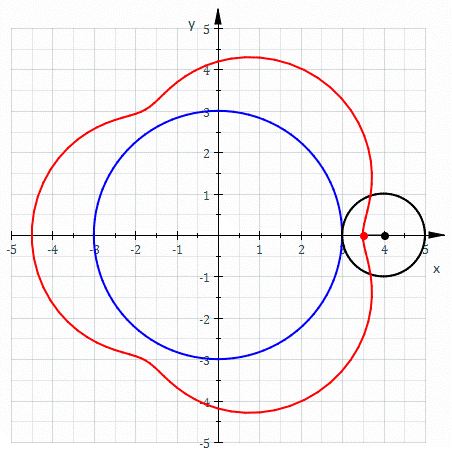
In geometry, a centered trochoid is the roulette formed by a circle rolling along another circle. That is, it is the path traced by a point attached to a circle as the circle rolls without slipping along a fixed circle. The term encompasses both epitrochoid and hypotrochoid. The center of this curve is defined to be the center of the fixed circle. Alternatively, a centered trochoid can be defined as the path traced by the sum of two vectors, each moving at a uniform speed in a circle. Specifically, a centered trochoid is a curve that can be parameterized in the complex plane by : z = r_1 e^ + r_2 e^,\, or in the Cartesian plane by : x = r_1 \cos(\omega_1 t) + r_2 \cos(\omega_2 t), :y = r_1 \sin(\omega_1 t) + r_2 \sin(\omega_2 t),\, where : r_1, r_2, \omega_1, \omega_2 \ne 0, \quad \omega_1 \ne \omega_2.\, If \omega_1/\omega_2 is rational then the curve is closed and algebraic. Otherwise the curve winds around the origin an infinite number of times, and is dense in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. On a basic level, it is the path traced by a curve while rolling on another curve without slipping. Definition Informal definition Roughly speaking, a roulette is the curve described by a point (called the ''generator'' or ''pole'') attached to a given curve as that curve rolls without slipping, along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls, without slipping, along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve, in the fixed plane called a roulette. Special cases and related concepts In the case where the rolling curve is a line and the generator is a point on the line, the roulette is called an involute of the fixed curve. If the rol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
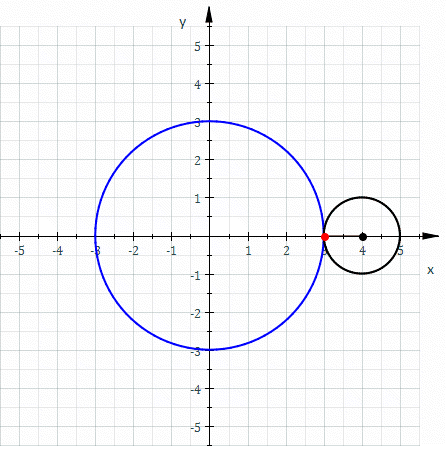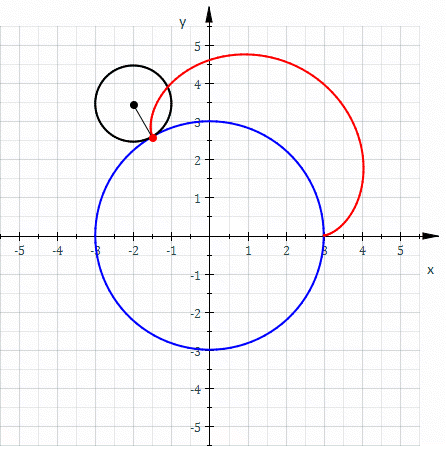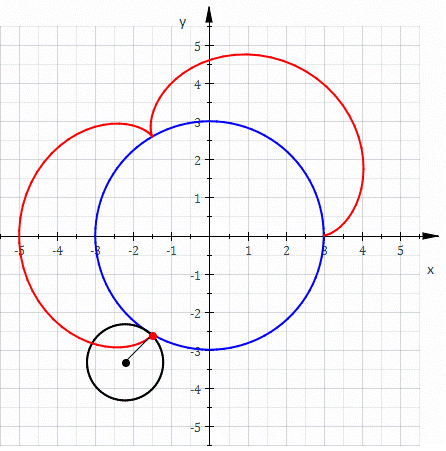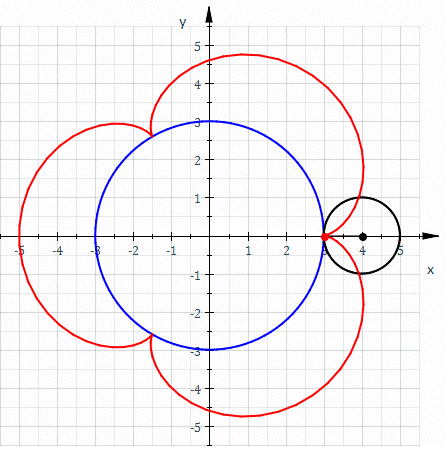
Epitrochoid
In geometry, an epitrochoid ( or ) is a roulette traced by a point attached to a circle of radius rolling around the outside of a fixed circle of radius , where the point is at a distance from the center of the exterior circle. The parametric equations for an epitrochoid are: :\begin & x (\theta) = (R + r)\cos\theta - d\cos\left(\theta\right) \\ & y (\theta) = (R + r)\sin\theta - d\sin\left(\theta\right) \end The parameter is geometrically the polar angle of the center of the exterior circle. (However, is not the polar angle of the point (x(\theta),y(\theta)) on the epitrochoid.) Special cases include the limaçon with and the epicycloid with . The classic Spirograph toy traces out epitrochoid and hypotrochoid curves. The paths of planets in the once popular geocentric system of deferents and epicycles are epitrochoids with d>r, for both the outer planets and the inner planets. The orbit of the Moon, when centered around the Sun, approximates an epitrochoid. The com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypotrochoid
In geometry, a hypotrochoid is a roulette (curve), roulette traced by a point attached to a circle of radius rolling around the inside of a fixed circle of radius , where the point is a distance from the center of the interior circle. The parametric equations for a hypotrochoid are: :\begin & x (\theta) = (R - r)\cos\theta + d\cos\left(\theta\right) \\ & y (\theta) = (R - r)\sin\theta - d\sin\left(\theta\right) \end where is the angle formed by the horizontal and the center of the rolling circle (these are not polar equations because is not the polar angle). When measured in radian, takes values from 0 to 2 \pi \times \tfrac (where is least common multiple). Special cases include the hypocycloid with and the ellipse with and . The eccentricity of the ellipse is :e=\frac becoming 1 when d=r (see Tusi couple). The classic Spirograph toy traces out hypotrochoid and epitrochoid curves. Hypotrochoids describe the support of the eigenvalues of some random matrices with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, called the imaginary axis, is formed by the imaginary numbers. The complex plane allows for a geometric interpretation of complex numbers. Under addition, they add like vector (geometry), vectors. The multiplication of two complex numbers can be expressed more easily in polar coordinates: the magnitude or ' of the product is the product of the two absolute values, or moduli, and the angle or ' of the product is the sum of the two angles, or arguments. In particular, multiplication by a complex number of modulus 1 acts as a rotation. The complex plane is sometimes called the Argand plane or Gauss plane. Notational conventions Complex numbers In complex analysis, the complex numbers are customarily represented by the symbol , which can be sepa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annulus (mathematics)
In mathematics, an annulus (: annuli or annuluses) is the region between two concentric circles. Informally, it is shaped like a ring or a hardware washer. The word "annulus" is borrowed from the Latin word ''anulus'' or ''annulus'' meaning 'little ring'. The adjectival form is ''annular'' (as in annular eclipse). The open annulus is topologically equivalent to both the open cylinder and the punctured plane. Area The area of an annulus is the difference in the areas of the larger circle of radius and the smaller one of radius : :A = \pi R^2 - \pi r^2 = \pi\left(R^2 - r^2\right) = \pi (R+r)(R-r) . The area of an annulus is determined by the length of the longest line segment within the annulus, which is the chord tangent to the inner circle, in the accompanying diagram. That can be shown using the Pythagorean theorem since this line is tangent to the smaller circle and perpendicular to its radius at that point, so and are sides of a right-angled triangle with hyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frank Morley
Frank Morley (September 9, 1860 – October 17, 1937) was a leading mathematician, known mostly for his teaching and research in the fields of algebra and geometry. Among his mathematical accomplishments was the discovery and proof of the celebrated Morley's trisector theorem in elementary plane geometry. He led 50 Ph.D. students, including Clara Latimer Bacon, to their degrees, and was said to be :... one of the more striking figures of the relatively small group of men who initiated that development which, within his own lifetime, brought Mathematics in America from a minor position to its present place in the sun. Life Morley was born in the town of Woodbridge in Suffolk, England. His parents were Elizabeth Muskett and Joseph Roberts Morley, Quakers who ran a china shop. After being educated at Woodbridge School, Morley went on to King's College, Cambridge (B.A., 1884). In 1887, Morley moved to Pennsylvania. He taught at Haverford College until 1900, when he became ch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. On a basic level, it is the path traced by a curve while rolling on another curve without slipping. Definition Informal definition Roughly speaking, a roulette is the curve described by a point (called the ''generator'' or ''pole'') attached to a given curve as that curve rolls without slipping, along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls, without slipping, along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve, in the fixed plane called a roulette. Special cases and related concepts In the case where the rolling curve is a line and the generator is a point on the line, the roulette is called an involute of the fixed curve. If the roll ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardioid
In geometry, a cardioid () is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle. The name was coined by Giovanni Salvemini in 1741 but the cardioid had been the subject of study decades beforehand.Yates Although named for its heart-like form, it is shaped more like the outline of the cross-section of a round apple without the stalk. A cardioid microphone exhibits an acoustic pickup pattern that, when graphed in two dimensions, resembles a cardioid (any 2d plane containing the 3d straight line of the microphone body). In three dimensions, the cardioid is shaped like an apple centred around the mic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hula Hoop
A hula hoop is a toy hoop (rhythmic gymnastics), hoop that is twirled around the waist, limbs or neck. It can also be wheeled along the ground like a wheel with careful execution and practice. They have been used by children and adults since at least 500 BC. The modern hula hoop was inspired by Australian bamboo hoops. Common lore posits the creators of the plastic hoop witnessed Australian children playing with bamboo hoops while driving past in an automobile. The new plastic version was popularized in 1958 by the Wham-O toy company and became a fad. Hula hoops for children generally measure approximately in diameter, while those for adults measure around . Traditional materials for hula hoops include willow, rattan (a flexible and strong vine), grapevines and stiff grasses. Commercial hoops are usually made of plastic tubing. Origins Native American Hoop Dance is a form of storytelling dance incorporating hoops as props. These props are used to create both static and dyna ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |