|
Cayley–Bacharach Theorem
In mathematics, the Cayley–Bacharach theorem is a statement about cubic curves (plane curves of degree three) in the projective plane . The original form states: :Assume that two cubics and in the projective plane meet in nine (different) points, as they do in general over an algebraically closed field. Then every cubic that passes through any eight of the points also passes through the ninth point. A more intrinsic form of the Cayley–Bacharach theorem reads as follows: :Every cubic curve over an algebraically closed field that passes through a given set of eight points also passes through (counting multiplicities) a ninth point which depends only on . A related result on conics was first proved by the French geometer Michel Chasles and later generalized to cubics by Arthur Cayley and Isaak Bacharach. Details If seven of the points lie on a conic, then the ninth point can be chosen on that conic, since will always contain the whole conic on account of Bézout's the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pascal's Theorem
In projective geometry, Pascal's theorem (also known as the ''hexagrammum mysticum theorem'') states that if six arbitrary points are chosen on a conic (which may be an ellipse, parabola or hyperbola in an appropriate affine plane) and joined by line segments in any order to form a hexagon, then the three pairs of opposite sides of the hexagon ( extended if necessary) meet at three points which lie on a straight line, called the Pascal line of the hexagon. It is named after Blaise Pascal. The theorem is also valid in the Euclidean plane, but the statement needs to be adjusted to deal with the special cases when opposite sides are parallel. This theorem is a generalization of Pappus's (hexagon) theorem, which is the special case of a degenerate conic of two lines with three points on each line. Euclidean variants The most natural setting for Pascal's theorem is in a projective plane since any two lines meet and no exceptions need to be made for parallel lines. However, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press A university press is an academic publishing house specializing in monographs and scholarly journals. Most are nonprofit organizations and an integral component of a large research university. They publish work that has been reviewed by schola ... in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 Country, countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematische Annalen
''Mathematische Annalen'' (abbreviated as ''Math. Ann.'' or, formerly, ''Math. Annal.'') is a German mathematical research journal founded in 1868 by Alfred Clebsch and Carl Neumann. Subsequent managing editors were Felix Klein, David Hilbert, Otto Blumenthal, Erich Hecke, Heinrich Behnke, Hans Grauert, Heinz Bauer, Herbert Amann, Jean-Pierre Bourguignon, Wolfgang Lück, and Nigel Hitchin. Currently, the managing editor of Mathematische Annalen is Thomas Schick. Volumes 1–80 (1869–1919) were published by Teubner. Since 1920 (vol. 81), the journal has been published by Springer. In the late 1920s, under the editorship of Hilbert, the journal became embroiled in controversy over the participation of L. E. J. Brouwer on its editorial board, a spillover from the foundational Brouwer–Hilbert controversy. Between 1945 and 1947 the journal briefly ceased publication. References External links''Mathematische Annalen''homepage at Springer''Mathematische Annalen''archive (1869†... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear System Of Divisors
In algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family. These arose first in the form of a ''linear system'' of algebraic curves in the projective plane. It assumed a more general form, through gradual generalisation, so that one could speak of linear equivalence of divisors ''D'' on a general scheme or even a ringed space (''X'', ''O''''X''). Linear system of dimension 1, 2, or 3 are called a pencil, a net, or a web, respectively. A map determined by a linear system is sometimes called the Kodaira map. Definition Given the fundamental idea of a rational function on a general variety X, or in other words of a function f in the function field of X, f \in k(X), divisors D,E \in \text(X) are linearly equivalent divisors if :D = E + (f)\ where (f) denotes the divisor of zeroes and poles of the function f. Note that i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monomial
In mathematics, a monomial is, roughly speaking, a polynomial which has only one term. Two definitions of a monomial may be encountered: # A monomial, also called power product, is a product of powers of variables with nonnegative integer exponents, or, in other words, a product of variables, possibly with repetitions. For example, x^2yz^3=xxyzzz is a monomial. The constant 1 is a monomial, being equal to the empty product and to x^0 for any variable x. If only a single variable x is considered, this means that a monomial is either 1 or a power x^n of x, with n a positive integer. If several variables are considered, say, x, y, z, then each can be given an exponent, so that any monomial is of the form x^a y^b z^c with a,b,c non-negative integers (taking note that any exponent 0 makes the corresponding factor equal to 1). # A monomial is a monomial in the first sense multiplied by a nonzero constant, called the coefficient of the monomial. A monomial in the first sense is a special c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameter Space
The parameter space is the space of possible parameter values that define a particular mathematical model, often a subset of finite-dimensional Euclidean space. Often the parameters are inputs of a function, in which case the technical term for the parameter space is domain of a function. The ranges of values of the parameters may form the axes of a plot, and particular outcomes of the model may be plotted against these axes to illustrate how different regions of the parameter space produce different types of behavior in the model. In statistics, parameter spaces are particularly useful for describing parametric families of probability distributions. They also form the background for parameter estimation. In the case of extremum estimators for parametric models, a certain objective function is maximized or minimized over the parameter space. Theorems of existence and consistency of such estimators require some assumptions about the topology of the parameter space. For instance, com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
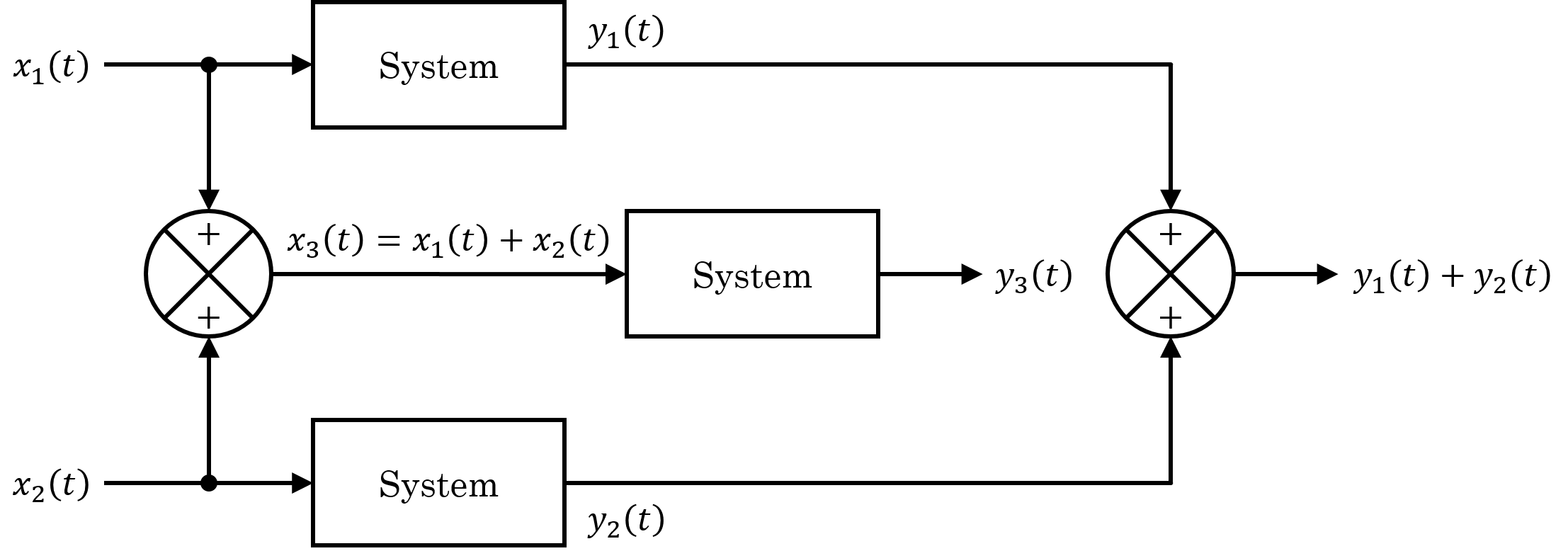
Linear System
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems. Definition A general deterministic system can be described by an operator, that maps an input, as a function of to an output, a type of black box description. A system is linear if and only if it satisfies the superposition principle, or equivalently both the additivity and homogeneity properties, without restrictions (that is, for all inputs, all scaling constants and all time.) The superposition principle means that a linear combination of inputs to the system produces a linear combination ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pencil (mathematics)
In geometry, a pencil is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a plane, or the set of circles that pass through two given points in a plane. Although the definition of a pencil is rather vague, the common characteristic is that the pencil is completely determined by any two of its members. Analogously, a set of geometric objects that are determined by any three of its members is called a bundle. Thus, the set of all lines through a point in three-space is a bundle of lines, any two of which determine a pencil of lines. To emphasize the two dimensional nature of such a pencil, it is sometimes referred to as a ''flat pencil''. Any geometric object can be used in a pencil. The common ones are lines, planes, circles, conics, spheres, and general curves. Even points can be used. A pencil of points is the set of all points on a given line. A more common term for this set is a ''range'' of points. Penci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann–Roch Theorem For Surfaces
In mathematics, the Riemann–Roch theorem for surfaces describes the dimension of linear systems on an algebraic surface. The classical form of it was first given by , after preliminary versions of it were found by and . The sheaf-theoretic version is due to Hirzebruch. Statement One form of the Riemann–Roch theorem states that if ''D'' is a divisor on a non-singular projective surface then :\chi(D) = \chi(0) +\tfrac D . (D - K) \, where χ is the holomorphic Euler characteristic, the dot . is the intersection number, and ''K'' is the canonical divisor. The constant χ(0) is the holomorphic Euler characteristic of the trivial bundle, and is equal to 1 + ''p''''a'', where ''p''''a'' is the arithmetic genus of the surface. For comparison, the Riemann–Roch theorem for a curve states that χ(''D'') = χ(0) + deg(''D''). Noether's formula Noether's formula states that :\chi = \frac = \frac where χ=χ(0) is the hol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overdetermined System
In mathematics, a system of equations is considered overdetermined if there are more equations than unknowns. An overdetermined system is almost always inconsistent (it has no solution) when constructed with random coefficients. However, an overdetermined system will have solutions in some cases, for example if some equation occurs several times in the system, or if some equations are linear combinations of the others. The terminology can be described in terms of the concept of constraint counting. Each unknown can be seen as an available degree of freedom. Each equation introduced into the system can be viewed as a constraint that restricts one degree of freedom. Therefore, the critical case occurs when the number of equations and the number of free variables are equal. For every variable giving a degree of freedom, there exists a corresponding constraint. The ''overdetermined'' case occurs when the system has been overconstrained — that is, when the equations outnumb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Position
In algebraic geometry and computational geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the ''general case'' situation, as opposed to some more special or coincidental cases that are possible, which is referred to as special position. Its precise meaning differs in different settings. For example, generically, two lines in the plane intersect in a single point (they are not parallel or coincident). One also says "two generic lines intersect in a point", which is formalized by the notion of a generic point. Similarly, three generic points in the plane are not collinear; if three points are collinear (even stronger, if two coincide), this is a degenerate case. This notion is important in mathematics and its applications, because degenerate cases may require an exceptional treatment; for example, when stating general theorems or giving precise statements thereof, and when writing computer programs (see '' generic compl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
