|
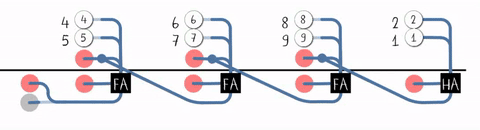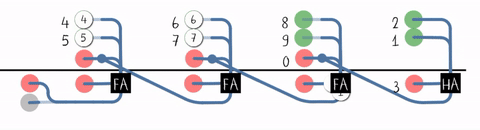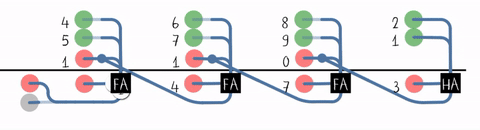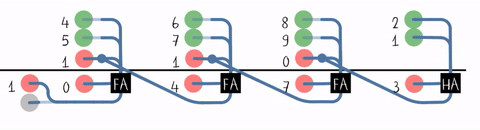
Carry-save Adder
A carry-save adder is a type of digital adder, used to efficiently compute the sum of three or more binary numbers. It differs from other digital adders in that it outputs two (or more) numbers, and the answer of the original summation can be achieved by adding these outputs together. A carry save adder is typically used in a binary multiplier, since a binary multiplier involves addition of more than two binary numbers after multiplication. A big adder implemented using this technique will usually be much faster than conventional addition of those numbers. Motivation Consider the sum: 12345678 + 87654322 = 100000000 Using basic arithmetic, we calculate right to left, "8 + 2 = 0, carry 1", "7 + 2 + 1 = 0, carry 1", "6 + 3 + 1 = 0, carry 1", and so on to the end of the sum. Although we know the last digit of the result at once, we cannot know the first digit until we have gone through every digit in the calculation, passing the carry from each digit to the one on its left. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Adder (electronics)
An adder, or summer, is a digital circuit that performs addition of numbers. In many computers and other kinds of microprocessor, processors, adders are used in the arithmetic logic units (ALUs). They are also used in other parts of the processor, where they are used to calculate address space, addresses, database index, table indices, increment and decrement operators and similar operations. Although adders can be constructed for many number representations, such as binary-coded decimal or excess-3, the most common adders operate on binary numbers. In cases where two's complement or ones' complement is being used to represent negative numbers, it is trivial to modify an adder into an adder–subtractor. Other signed number representations require more logic around the basic adder. History George Stibitz invented the 2-bit binary adder (the Model K (calculator), Model K) in 1937. Binary adders Half adder The half adder adds two single binary digits A and B. It has two outputs, s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Binary Numeral System
A binary number is a number expressed in the base-2 numeral system or binary numeral system, a method for representing numbers that uses only two symbols for the natural numbers: typically "0" ( zero) and "1" ( one). A ''binary number'' may also refer to a rational number that has a finite representation in the binary numeral system, that is, the quotient of an integer by a power of two. The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit, or binary digit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation. History The modern binary number system was studied in Europe in the 16th and 17th centuries by Thomas Harrio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Carry Look-ahead Adder
A carry-lookahead adder (CLA) or fast adder is a type of electronics adder used in digital logic. A carry-lookahead adder improves speed by reducing the amount of time required to determine carry bits. It can be contrasted with the simpler, but usually slower, ripple-carry adder (RCA), for which the carry bit is calculated alongside the sum bit, and each stage must wait until the previous carry bit has been calculated to begin calculating its own sum bit and carry bit. The carry-lookahead adder calculates one or more carry bits before the sum, which reduces the wait time to calculate the result of the larger-value bits of the adder. Already in the mid-1800s, Charles Babbage recognized the performance penalty imposed by the ripple-carry used in his Difference Engine, and subsequently designed mechanisms for ''anticipating carriage'' for his never-built Analytical Engine. Konrad Zuse is thought to have implemented the first carry-lookahead adder in his 1930s binary mechanical com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Public-key Cryptography
Public-key cryptography, or asymmetric cryptography, is the field of cryptographic systems that use pairs of related keys. Each key pair consists of a public key and a corresponding private key. Key pairs are generated with cryptographic algorithms based on mathematical problems termed one-way functions. Security of public-key cryptography depends on keeping the private key secret; the public key can be openly distributed without compromising security. There are many kinds of public-key cryptosystems, with different security goals, including digital signature, Diffie–Hellman key exchange, Key encapsulation mechanism, public-key key encapsulation, and public-key encryption. Public key algorithms are fundamental security primitives in modern cryptosystems, including applications and protocols that offer assurance of the confidentiality and authenticity of electronic communications and data storage. They underpin numerous Internet standards, such as Transport Layer Security, T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
John Von Neumann
John von Neumann ( ; ; December 28, 1903 – February 8, 1957) was a Hungarian and American mathematician, physicist, computer scientist and engineer. Von Neumann had perhaps the widest coverage of any mathematician of his time, integrating Basic research, pure and Applied science#Applied research, applied sciences and making major contributions to many fields, including mathematics, physics, economics, computing, and statistics. He was a pioneer in building the mathematical framework of quantum physics, in the development of functional analysis, and in game theory, introducing or codifying concepts including Cellular automaton, cellular automata, the Von Neumann universal constructor, universal constructor and the Computer, digital computer. His analysis of the structure of self-replication preceded the discovery of the structure of DNA. During World War II, von Neumann worked on the Manhattan Project. He developed the mathematical models behind the explosive lense ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Redundant Binary Representation
A redundant binary representation (RBR) is a numeral system that uses more bits than needed to represent a single binary digit so that most numbers have several representations. An RBR is unlike usual binary numeral systems, including two's complement, which use a single bit for each digit. Many of an RBR's properties differ from those of regular binary representation systems. Most importantly, an RBR allows addition without using a typical carry. When compared to non-redundant representation, an RBR makes bitwise logical operation slower, but arithmetic operations are faster when a greater bit width is used. Usually, each digit has its own sign that is not necessarily the same as the sign of the number represented. When digits have signs, that RBR is also a signed-digit representation. Conversion from RBR An RBR is a place-value notation system. In an RBR, digits are ''pairs'' of bits, that is, for every place, an RBR uses a pair of bits. The value represented by a redundant dig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Montgomery Multiplication
Montgomery refers to: People For people with the name Montgomery, see Montgomery (name) Places Belgium * Montgomery Square, Brussels * Montgomery metro station, Brussels Pakistan * Montgomery (town), British India, former name of Sahiwal, Punjab * Montgomery District, an administrative district in the Lahore division of former Punjab Province of British India ** Montgomery Tahsil, an administrative subdivision of Montgomery District in Punjab province of British India United Kingdom Wales * Montgomery, Powys ** Montgomery Canal ** Montgomery Castle * Montgomeryshire (other) United States * Montgomery, Alabama, state capital * Montgomery, Georgia * Montgomery, Illinois * Montgomery, Indiana * Montgomery, Iowa * Montgomery, Kentucky * Montgomery, Louisiana * Montgomery, Massachusetts * Montgomery, Michigan * Montgomery, Minnesota * Montgomery, Mississippi * Montgomery, New York (other) * Montgomery, Ohio * Montgomery, Pennsylvania * Montgomery, Tennessee * Montgo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Logical Shift
In computer science, a logical shift is a bitwise operation that shifts all the bits of its operand. The two base variants are the logical left shift and the logical right shift. This is further modulated by the number of bit positions a given value shall be shifted, such as ''shift left by 1'' or ''shift right by n''. Unlike an arithmetic shift, a logical shift does not preserve a number's sign bit or distinguish a number's exponent from its significand (mantissa); every bit in the operand is simply moved a given number of bit positions, and the vacant bit-positions are filled, usually with zeros, and possibly ones (contrast with a circular shift). A logical shift is often used when its operand is being treated as a sequence of bits instead of as a number. Logical shifts can be useful as efficient ways to perform multiplication or division of unsigned integers by powers of two. Shifting left by ''n'' bits on a signed or unsigned binary number has the effect of multiplyin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Most Significant Bit
In computing, bit numbering is the convention used to identify the bit positions in a binary numeral system, binary number. Bit significance and indexing In computing, the least significant bit (LSb) is the bit position in a Binary numeral system, binary Integer (computer science), integer representing the lowest-order place of the integer. Similarly, the most significant bit (MSb) represents the highest-order place of the binary integer. The LSb is sometimes referred to as the ''low-order bit''. Due to the convention in positional notation of writing less significant digits further to the right, the LSb also might be referred to as the ''right-most bit''. The MSb is similarly referred to as the ''high-order bit'' or ''left-most bit''. In both cases, the LSb and MSb correlate directly to the least significant Numerical digit, digit and most significant digit of a decimal integer. Bit indexing correlates to the positional notation of the value in base 2. For this reason, bit in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Adder (electronics)
An adder, or summer, is a digital circuit that performs addition of numbers. In many computers and other kinds of microprocessor, processors, adders are used in the arithmetic logic units (ALUs). They are also used in other parts of the processor, where they are used to calculate address space, addresses, database index, table indices, increment and decrement operators and similar operations. Although adders can be constructed for many number representations, such as binary-coded decimal or excess-3, the most common adders operate on binary numbers. In cases where two's complement or ones' complement is being used to represent negative numbers, it is trivial to modify an adder into an adder–subtractor. Other signed number representations require more logic around the basic adder. History George Stibitz invented the 2-bit binary adder (the Model K (calculator), Model K) in 1937. Binary adders Half adder The half adder adds two single binary digits A and B. It has two outputs, s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Wallace Tree
A Wallace multiplier is a hardware implementation of a binary multiplier, a digital circuit that multiplies two integers. It uses a selection of full and half adders (the Wallace tree or Wallace reduction) to sum partial products in stages until two numbers are left. Wallace multipliers reduce as much as possible on each layer, whereas Dadda multipliers try to minimize the required number of gates by postponing the reduction to the upper layers. Wallace multipliers were devised by the Australian computer scientist Chris Wallace in 1964. The Wallace tree has three steps: # Multiply each bit of one of the arguments, by each bit of the other. # Reduce the number of partial products to two by layers of full and half adders. # Group the wires in two numbers, and add them with a conventional adder. Compared to naively adding partial products with regular adders, the benefit of the Wallace tree is its faster speed. It has O(\log n) reduction layers, but each layer has only O(1) p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Carry-skip Adder
A carry-skip adder (also known as a carry-bypass adder) is an adder implementation that improves on the delay of a ripple-carry adder with little effort compared to other adders. The improvement of the worst-case delay is achieved by using several carry-skip adders to form a block-carry-skip adder. Unlike other fast adders, carry-skip adder performance is increased with only some of the combinations of input bits. This means, speed improvement is only probabilistic. Single carry-skip adder The worst case for a simple one level ripple-carry adder occurs, when the propagate-condition is true for each digit pair (a_i, b_i). Then the carry-in ripples through the n-bit adder and appears as the carry-out after \tau_(n) \approx n \cdot \tau_. For each operand input bit pair (a_i,b_i) the propagate-conditions p_i = a_i \oplus b_i are determined using an XOR-gate. When all propagate-conditions are ''true'', then the carry-in bit c_0 determines the carry-out bit. The ''n''-bit-carry-sk ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |