|
Algorithmic Inference
Algorithmic inference gathers new developments in the statistical inference methods made feasible by the powerful computing devices widely available to any data analyst. Cornerstones in this field are computational learning theory, granular computing, bioinformatics, and, long ago, structural probability . The main focus is on the algorithms which compute statistics rooting the study of a random phenomenon, along with the amount of data they must feed on to produce reliable results. This shifts the interest of mathematicians from the study of the distribution laws to the functional properties of the statistics, and the interest of computer scientists from the algorithms for processing data to the information they process. The Fisher parametric inference problem Concerning the identification of the parameters of a distribution law, the mature reader may recall lengthy disputes in the mid 20th century about the interpretation of their variability in terms of fiducial distribution , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Inference
Statistical inference is the process of using data analysis to infer properties of an underlying probability distribution.Upton, G., Cook, I. (2008) ''Oxford Dictionary of Statistics'', OUP. . Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population. Inferential statistics can be contrasted with descriptive statistics. Descriptive statistics is solely concerned with properties of the observed data, and it does not rest on the assumption that the data come from a larger population. In machine learning, the term ''inference'' is sometimes used instead to mean "make a prediction, by evaluating an already trained model"; in this context inferring properties of the model is referred to as ''training'' or ''learning'' (rather than ''inference''), and using a model for prediction is referred to as ''inference'' (instead of ''prediction''); se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complexity
Complexity characterizes the behavior of a system or model whose components interact in multiple ways and follow local rules, leading to non-linearity, randomness, collective dynamics, hierarchy, and emergence. The term is generally used to characterize something with many parts where those parts interact with each other in multiple ways, culminating in a higher order of emergence greater than the sum of its parts. The study of these complex linkages at various scales is the main goal of complex systems theory. The intuitive criterion of complexity can be formulated as follows: a system would be more complex if more parts could be distinguished, and if more connections between them existed. , a number of approaches to characterizing complexity have been used in science; Zayed ''et al.'' reflect many of these. Neil Johnson states that "even among scientists, there is no unique definition of complexity – and the scientific notion has traditionally been conveyed using partic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Twisting Properties
Twisting properties in general terms are associated with the properties of samples that identify with statistics that are suitable for exchange. Description Starting with a sample \ observed from a random variable ''X'' having a given distribution law with a non-set parameter, a parametric inference problem consists of computing suitable values – call them estimates – of this parameter precisely on the basis of the sample. An estimate is suitable if replacing it with the unknown parameter does not cause major damage in next computations. In algorithmic inference, suitability of an estimate reads in terms of compatibility with the observed sample. In turn, parameter compatibility is a probability measure that we derive from the probability distribution of the random variable to which the parameter refers. In this way we identify a random parameter Θ compatible with an observed sample. Given a sampling mechanism M_X=(g_\theta,Z), the rationale of this operation lies in us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bootstrapping Populations
Bootstrapping populations in statistics and mathematics starts with a Statistical sample, sample \ observed from a random variable. When ''X'' has a given cumulative distribution function, distribution law with a set of non fixed parameters, we denote with a vector \boldsymbol\theta, a Parametric statistics, parametric inference problem consists of computing suitable values – call them estimator, estimates – of these parameters precisely on the basis of the sample. An estimate is suitable if replacing it with the unknown parameter does not cause major damage in next computations. In Algorithmic inference, suitability of an estimate reads in terms of Algorithmic inference#compatible distribution, compatibility with the observed sample. In this framework, Resampling (statistics), resampling methods are aimed at generating a set of candidate values to replace the unknown parameters that we read as compatible replicas of them. They represent a population of specifications of a ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Well-behaved Statistic
Although the term well-behaved statistic often seems to be used in the scientific literature in somewhat the same way as is well-behaved in mathematics (that is, to mean "non- pathological") it can also be assigned precise mathematical meaning, and in more than one way. In the former case, the meaning of this term will vary from context to context. In the latter case, the mathematical conditions can be used to derive classes of combinations of distributions with statistics which are ''well-behaved'' in each sense. First Definition: The variance of a well-behaved statistical estimator is finite and one condition on its mean is that it is differentiable in the parameter being estimated. Second Definition: The statistic is monotonic, well-defined, and locally sufficient. Conditions for a Well-Behaved Statistic: First Definition More formally the conditions can be expressed in this way. T is a statistic for \theta that is a function of the sample, _,...,_. For T to be ''well-behaved ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sufficient Statistics
In logic and mathematics, necessity and sufficiency are terms used to describe a conditional or implicational relationship between two statements. For example, in the conditional statement: "If then ", is necessary for , because the truth of is guaranteed by the truth of . (Equivalently, it is impossible to have without , or the falsity of ensures the falsity of .) Similarly, is sufficient for , because being true always implies that is true, but not being true does not always imply that is not true. In general, a necessary condition is one (possibly one of several conditions) that must be present in order for another condition to occur, while a sufficient condition is one that produces the said condition. The assertion that a statement is a "necessary ''and'' sufficient" condition of another means that the former statement is true if and only if the latter is true. That is, the two statements must be either simultaneously true, or simultaneously false. In ordinary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pareto Distribution
The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto, is a power-law probability distribution that is used in description of social, quality control, scientific, geophysical, actuarial science, actuarial, and many other types of observable phenomena; the principle originally applied to describing the distribution of wealth in a society, fitting the trend that a large portion of wealth is held by a small fraction of the population. The ''Pareto principle'' or "80:20 rule" stating that 80% of outcomes are due to 20% of causes was named in honour of Pareto, but the concepts are distinct, and only Pareto distributions with shape value () precisely reflect it. Empirical observation has shown that this 80:20 distribution fits a wide range of cases, including natural phenomena and human activities. Definitions If ''X'' is a random variable with a Pareto (Type I) distribution, then the probability that ''X'' is greater than some nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Distribution (continuous)
In probability theory and statistics, the continuous uniform distributions or rectangular distributions are a family of symmetric probability distributions. Such a distribution describes an experiment where there is an arbitrary outcome that lies between certain bounds. The bounds are defined by the parameters, a and b, which are the minimum and maximum values. The interval can either be closed (i.e. ,b/math>) or open (i.e. (a,b)). Therefore, the distribution is often abbreviated U(a,b), where U stands for uniform distribution. The difference between the bounds defines the interval length; all intervals of the same length on the distribution's support are equally probable. It is the maximum entropy probability distribution for a random variable X under no constraint other than that it is contained in the distribution's support. Definitions Probability density function The probability density function of the continuous uniform distribution is f(x) = \begin \dfrac & ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
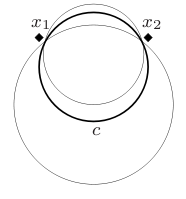
Complexity Index
In modern computer science and statistics, the complexity index of a function denotes the level of informational content, which in turn affects the difficulty of learning the function from examples. This is different from computational complexity, which is the difficulty to compute a function. Complexity indices characterize the entire class of functions to which the one we are interested in belongs. Focusing on Boolean functions, the ''detail'' of a class \mathsf C of Boolean functions ''c'' essentially denotes how deeply the class is articulated. Technical definition To identify this index we must first define a ''sentry function'' of \mathsf C. Let us focus for a moment on a single function ''c'', call it a ''concept'' defined on a set \mathcal X of elements that we may figure as points in a Euclidean space. In this framework, the above function associates to ''c'' a set of points that, since are defined to be external to the concept, prevent it from expanding into another funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
VC Dimension
VC may refer to: Military decorations * Victoria Cross, a military decoration awarded by the United Kingdom and other Commonwealth nations ** Victoria Cross for Australia ** Victoria Cross (Canada) ** Victoria Cross for New Zealand * Victorious Cross, Idi Amin's self-bestowed military decoration Organisations * Ocean Airlines (IATA airline designator 2003-2008), Italian cargo airline * Voyageur Airways (IATA airline designator since 1968), Canadian charter airline * Visual Communications, an Asian-Pacific-American media arts organization in Los Angeles, California * Viet Cong, a political and military organization during the Vietnam War (1959–1975) Education * Vanier College, Canada * Vassar College, US * Velez College, Philippines * Virginia College, US * Ventura College, US Places * Saint Vincent and the Grenadines (ISO country code) * Sri Lanka (ICAO airport prefix code) * Watsonian vice-counties, subdivisions of Great Britain or Ireland * Ventura County, in S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complexity Index
In modern computer science and statistics, the complexity index of a function denotes the level of informational content, which in turn affects the difficulty of learning the function from examples. This is different from computational complexity, which is the difficulty to compute a function. Complexity indices characterize the entire class of functions to which the one we are interested in belongs. Focusing on Boolean functions, the ''detail'' of a class \mathsf C of Boolean functions ''c'' essentially denotes how deeply the class is articulated. Technical definition To identify this index we must first define a ''sentry function'' of \mathsf C. Let us focus for a moment on a single function ''c'', call it a ''concept'' defined on a set \mathcal X of elements that we may figure as points in a Euclidean space. In this framework, the above function associates to ''c'' a set of points that, since are defined to be external to the concept, prevent it from expanding into another funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |