|
Branch And Cut
Branch and cut is a method of combinatorial optimization for solving integer linear programs (ILPs), that is, linear programming (LP) problems where some or all the unknowns are restricted to integer values. Branch and cut involves running a branch and bound algorithm and using cutting planes to tighten the linear programming relaxations. Note that if cuts are only used to tighten the initial LP relaxation, the algorithm is called branch and cut. Algorithm This description assumes the ILP is a maximization problem. The method solves the linear program without the integer constraint using the regular simplex algorithm. When an optimal solution is obtained, and this solution has a non-integer value for a variable that is supposed to be integer, a cutting plane algorithm may be used to find further linear constraints which are satisfied by all feasible integer points but violated by the current fractional solution. These inequalities may be added to the linear program, such that r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorial Optimization
Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combinatorial optimization problems are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem. In many such problems, such as the ones previously mentioned, exhaustive search is not tractable, and so specialized algorithms that quickly rule out large parts of the search space or approximation algorithms must be resorted to instead. Combinatorial optimization is related to operations research, algorithm theory, and computational complexity theory. It has important applications in several fields, including artificial intelligence, machine learning, auction theory, software engineering, VLSI, applied mathematics and theoretical computer science. Some research literature considers discrete o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Linear Program
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming (ILP), in which the objective function and the constraints (other than the integer constraints) are linear. Integer programming is NP-complete. In particular, the special case of 0-1 integer linear programming, in which unknowns are binary, and only the restrictions must be satisfied, is one of Karp's 21 NP-complete problems. If some decision variables are not discrete, the problem is known as a mixed-integer programming problem. Canonical and standard form for ILPs In integer linear programming, the ''canonical form'' is distinct from the ''standard form''. An integer linear program in canonical form is expressed thus (note that it is the \mathbf vector which is to be decided): : \begin & \text && \mathbf^\mathrm \mathbf\\ & \text && A \mathbf \le \mathbf, \\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear function#As a polynomial function, linear relationships. Linear programming is a special case of mathematical programming (also known as mathematical optimization). More formally, linear programming is a technique for the mathematical optimization, optimization of a linear objective function, subject to linear equality and linear inequality Constraint (mathematics), constraints. Its feasible region is a convex polytope, which is a set defined as the intersection (mathematics), intersection of finitely many Half-space (geometry), half spaces, each of which is defined by a linear inequality. Its objective function is a real number, real-valued affine function, affine (linear) function defined on this polyhedron. A linear programming algorithm finds a point in the polytope where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface or blackboard bold \mathbb. The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the natural numbers, \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general algebraic integers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Branch And Bound
Branch and bound (BB, B&B, or BnB) is an algorithm design paradigm for discrete and combinatorial optimization problems, as well as mathematical optimization. A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores ''branches'' of this tree, which represent subsets of the solution set. Before enumerating the candidate solutions of a branch, the branch is checked against upper and lower estimated ''bounds'' on the optimal solution, and is discarded if it cannot produce a better solution than the best one found so far by the algorithm. The algorithm depends on efficient estimation of the lower and upper bounds of regions/branches of the search space. If no bounds are available, the algorithm degenerates to an exhaustive search. The method was first proposed by Ailsa Land and Alison Doig whilst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
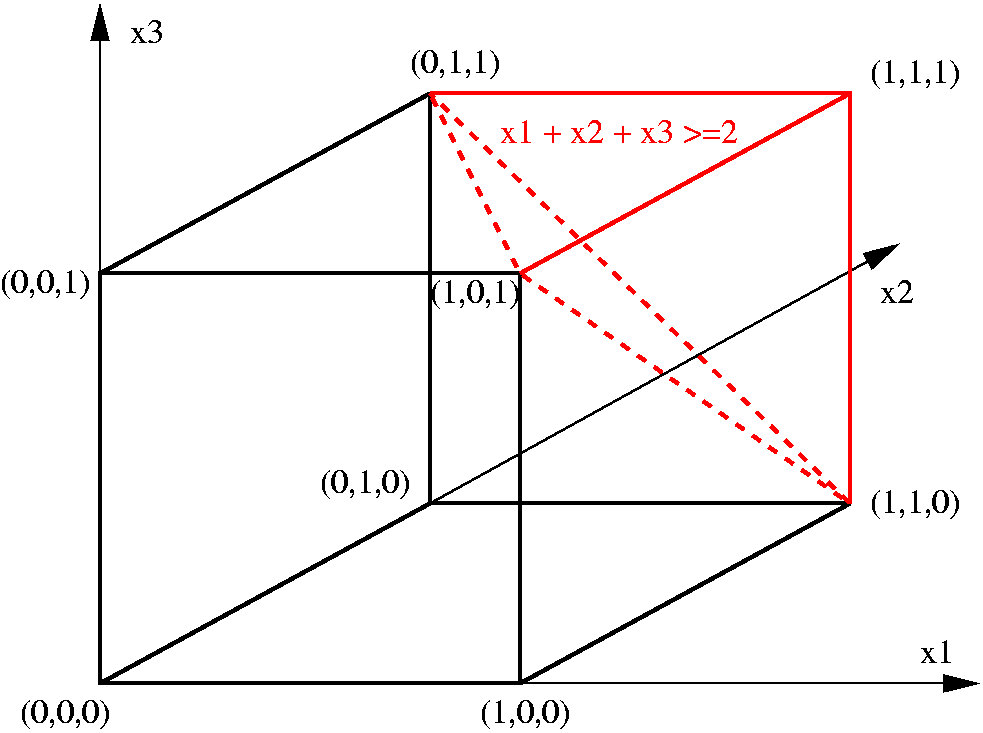
Cutting Plane
In mathematical optimization, the cutting-plane method is any of a variety of optimization methods that iteratively refine a feasible set or objective function by means of linear inequalities, termed ''cuts''. Such procedures are commonly used to find integer solutions to mixed integer linear programming (MILP) problems, as well as to solve general, not necessarily differentiable convex optimization problems. The use of cutting planes to solve MILP was introduced by Ralph E. Gomory. Cutting plane methods for MILP work by solving a non-integer linear program, the linear relaxation of the given integer program. The theory of Linear Programming dictates that under mild assumptions (if the linear program has an optimal solution, and if the feasible region does not contain a line), one can always find an extreme point or a corner point that is optimal. The obtained optimum is tested for being an integer solution. If it is not, there is guaranteed to exist a linear inequality that '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Programming Relaxation
In mathematics, the relaxation of a (mixed) integer linear program is the problem that arises by removing the integrality constraint of each variable. For example, in a 0–1 integer program, all constraints are of the form :x_i\in\. The relaxation of the original integer program instead uses a collection of linear constraints :0 \le x_i \le 1. The resulting relaxation is a linear program, hence the name. This relaxation technique transforms an NP-hard optimization problem (integer programming) into a related problem that is solvable in polynomial time (linear programming); the solution to the relaxed linear program can be used to gain information about the solution to the original integer program. Example Consider the set cover problem, the linear programming relaxation of which was first considered by . In this problem, one is given as input a family of sets ''F'' = ; the task is to find a subfamily, with as few sets as possible, having the same union as ''F''. To formulate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simplex Algorithm
In mathematical optimization, Dantzig's simplex algorithm (or simplex method) is a popular algorithm for linear programming. The name of the algorithm is derived from the concept of a simplex and was suggested by T. S. Motzkin. Simplices are not actually used in the method, but one interpretation of it is that it operates on simplicial ''cones'', and these become proper simplices with an additional constraint. The simplicial cones in question are the corners (i.e., the neighborhoods of the vertices) of a geometric object called a polytope. The shape of this polytope is defined by the constraints applied to the objective function. History George Dantzig worked on planning methods for the US Army Air Force during World War II using a desk calculator. During 1946 his colleague challenged him to mechanize the planning process to distract him from taking another job. Dantzig formulated the problem as linear inequalities inspired by the work of Wassily Leontief, however, at that t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cutting-plane Method
In mathematical optimization, the cutting-plane method is any of a variety of optimization methods that iteratively refine a feasible set or objective function by means of linear inequalities, termed ''cuts''. Such procedures are commonly used to find integer solutions to mixed integer linear programming (MILP) problems, as well as to solve general, not necessarily differentiable convex optimization problems. The use of cutting planes to solve MILP was introduced by Ralph E. Gomory. Cutting plane methods for MILP work by solving a non-integer linear program, the linear relaxation of the given integer program. The theory of Linear Programming dictates that under mild assumptions (if the linear program has an optimal solution, and if the feasible region does not contain a line), one can always find an extreme point or a corner point that is optimal. The obtained optimum is tested for being an integer solution. If it is not, there is guaranteed to exist a linear inequality that ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feasible Solution
In mathematical optimization, a feasible region, feasible set, search space, or solution space is the set of all possible points (sets of values of the choice variables) of an optimization problem that satisfy the problem's constraints, potentially including inequalities, equalities, and integer constraints. This is the initial set of candidate solutions to the problem, before the set of candidates has been narrowed down. For example, consider the problem of minimizing the function x^2+y^4 with respect to the variables x and y, subject to 1 \le x \le 10 and 5 \le y \le 12. \, Here the feasible set is the set of pairs (''x'', ''y'') in which the value of ''x'' is at least 1 and at most 10 and the value of ''y'' is at least 5 and at most 12. The feasible set of the problem is separate from the objective function, which states the criterion to be optimized and which in the above example is x^2+y^4. In many problems, the feasible set reflects a constraint that one or mor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
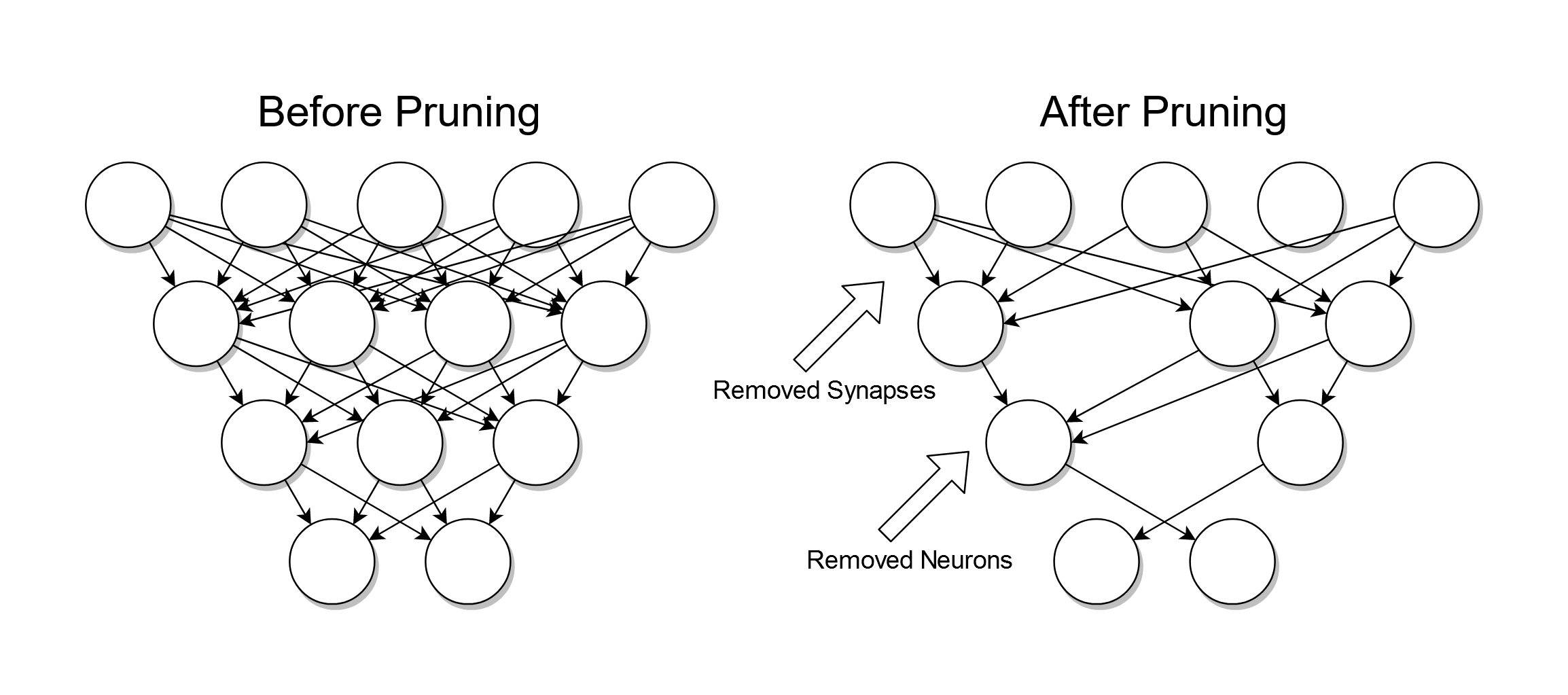
Search Tree Pruning
Pruning is a data compression technique in machine learning and search algorithms that reduces the size of decision trees by removing sections of the tree that are non-critical and redundant to classify instances. Pruning reduces the complexity of the final classifier, and hence improves predictive accuracy by the reduction of overfitting. One of the questions that arises in a decision tree algorithm is the optimal size of the final tree. A tree that is too large risks overfitting the training data and poorly generalizing to new samples. A small tree might not capture important structural information about the sample space. However, it is hard to tell when a tree algorithm should stop because it is impossible to tell if the addition of a single extra node will dramatically decrease error. This problem is known as the horizon effect. A common strategy is to grow the tree until each node contains a small number of instances then use pruning to remove nodes that do not provide ad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
While Loop
In most computer programming languages, a while loop is a control flow statement that allows code to be executed repeatedly based on a given Boolean condition. The ''while'' loop can be thought of as a repeating if statement. Overview The ''while'' construct consists of a block of code and a condition/expression. The condition/expression is evaluated, and if the condition/expression is ''true'', the code within all of their following in the block is executed. This repeats until the condition/expression becomes false. Because the ''while'' loop checks the condition/expression before the block is executed, the control structure is often also known as a pre-test loop. Compare this with the ''do while'' loop, which tests the condition/expression ''after'' the loop has executed. For example, in the C programming language (as well as Java, C#, Objective-C, and C++, which use the same syntax in this case), the code fragment int x = 0; while (x 0 loop Factorial := Fac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
