|
Bivariate (other)
{{disambiguation ...
Bivariate may refer to: Mathematics * Bivariate function, a function of two variables * Bivariate polynomial, a polynomial of two indeterminates Statistics * Bivariate data, that shows the relationship between two variables * Bivariate analysis, statistical analysis of two variables * Bivariate distribution, a joint probability distribution for two variables Other * Bivariate map, a single map that displays two variables See also * Two-dimensional curve * Multivariate (other) Multivariate may refer to: In mathematics * Multivariable calculus * Multivariate function * Multivariate polynomial In computing * Multivariate cryptography * Multivariate division algorithm * Multivariate interpolation * Multivariate optical c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bivariate Function
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the function and the set is called the codomain of the function.Codomain ''Encyclopedia of Mathematics'Codomain. ''Encyclopedia of Mathematics''/ref> The earliest known approach to the notion of function can be traced back to works of Persian mathematicians Al-Biruni and Sharaf al-Din al-Tusi. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bivariate Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. Etymology The word ''polynomial'' j ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
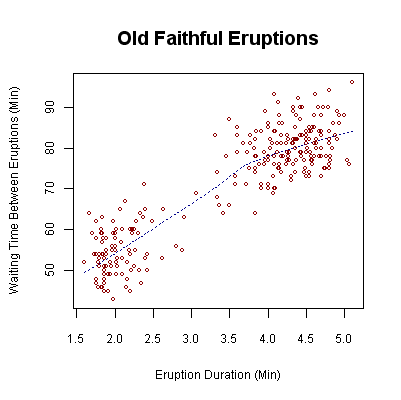
Bivariate Data
In statistics, bivariate data is data on each of two variables, where each value of one of the variables is paired with a value of the other variable. Typically it would be of interest to investigate the possible association between the two variables. The association can be studied via a tabular or graphical display, or via sample statistics which might be used for inference. The method used to investigate the association would depend on the level of measurement of the variable. This association that involves exactly two variables can be termed a bivariate correlation, or bivariate association. For two quantitative variables (interval or ratio in level of measurement) a scatterplot can be used and a correlation coefficient or regression model can be used to quantify the association. For two qualitative variables (nominal or ordinal in level of measurement) a contingency table can be used to view the data, and a measure of association or a test of independence could be used. If ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bivariate Analysis
Bivariate analysis is one of the simplest forms of quantitative (statistical) analysis.Earl R. Babbie, ''The Practice of Social Research'', 12th edition, Wadsworth Publishing, 2009, , pp. 436–440 It involves the analysis of two variables (often denoted as ''X'', ''Y''), for the purpose of determining the empirical relationship between them. Bivariate analysis can be helpful in testing simple hypotheses of association. Bivariate analysis can help determine to what extent it becomes easier to know and predict a value for one variable (possibly a dependent variable) if we know the value of the other variable (possibly the independent variable) (see also correlation and simple linear regression). Bivariate analysis can be contrasted with univariate analysis in which only one variable is analysed. Like univariate analysis, bivariate analysis can be descriptive or inferential. It is the analysis of the relationship between the two variables. Bivariate analysis is a simp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Joint Probability Distribution
Given two random variables that are defined on the same probability space, the joint probability distribution is the corresponding probability distribution on all possible pairs of outputs. The joint distribution can just as well be considered for any given number of random variables. The joint distribution encodes the marginal distributions, i.e. the distributions of each of the individual random variables. It also encodes the conditional probability distributions, which deal with how the outputs of one random variable are distributed when given information on the outputs of the other random variable(s). In the formal mathematical setup of measure theory, the joint distribution is given by the pushforward measure, by the map obtained by pairing together the given random variables, of the sample space's probability measure. In the case of real-valued random variables, the joint distribution, as a particular multivariate distribution, may be expressed by a multivariate cumulativ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bivariate Map
A bivariate map or multivariate map is a type of thematic map that displays two or more variables on a single map by combining different sets of symbols.Nelson, J. (2020)Multivariate Mapping ''The Geographic Information Science & Technology Body of Knowledge'' (1st Quarter 2020 Edition), John P. Wilson (ed.). DOI: 10.22224/gistbok/2020.1.5 Each of the variables is represented using a standard thematic map technique, such as choropleth, cartogram, or proportional symbols. They may be the same type or different types, and they may be on separate layers of the map, or they may be combined into a single multivariate symbol. The typical objective of a multivariate map is to visualize any statistical or geographic relationship between the variables. It has potential to reveal relationships between variables more effectively than a side-by-side comparison of the corresponding univariate maps, but also has the danger of Cognitive overload when the symbols and patterns are too co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-dimensional Curve
In mathematics, a plane curve is a curve in a plane that may be either a Euclidean plane, an affine plane or a projective plane. The most frequently studied cases are smooth plane curves (including piecewise smooth plane curves), and algebraic plane curves. Plane curves also include the Jordan curves (curves that enclose a region of the plane but need not be smooth) and the graphs of continuous functions. Symbolic representation A plane curve can often be represented in Cartesian coordinates by an implicit equation of the form f(x,y)=0 for some specific function ''f''. If this equation can be solved explicitly for ''y'' or ''x'' – that is, rewritten as y=g(x) or x=h(y) for specific function ''g'' or ''h'' – then this provides an alternative, explicit, form of the representation. A plane curve can also often be represented in Cartesian coordinates by a parametric equation of the form (x,y)=(x(t), y(t)) for specific functions x(t) and y(t). Plane curves can sometimes also be r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |