|
Burnside's Lemma
Burnside's lemma, sometimes also called Burnside's counting theorem, the Cauchy–Frobenius lemma, or the orbit-counting theorem, is a result in group theory that is often useful in taking account of symmetry when counting mathematical objects. It was discovered by Augustin Louis Cauchy and Ferdinand Georg Frobenius, and became well known after William Burnside quoted it. The result enumerates orbits of a symmetry group acting on some objects: that is, it counts distinct objects, considering objects symmetric to each other as the same; or counting distinct objects up to a symmetry equivalence relation; or counting only objects in canonical form. For example, in describing possible organic compounds of certain type, one considers them up to spatial rotation symmetry: different rotated drawings of a given molecule are chemically identical. (However a mirror reflection might give a different compound.) Formally, let G be a finite group that acts on a set X. For each g in G, le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field (mathematics), fields, and vector spaces, can all be seen as groups endowed with additional operation (mathematics), operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right. Various physical systems, such as crystals and the hydrogen atom, and Standard Model, three of the four known fundamental forces in the universe, may be modelled by symmetry groups. Thus group theory and the closely related representation theory have many important applications in physics, chemistry, and materials science. Group theory is also cen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit (group Theory)
In mathematics, a group action of a group G on a set S is a group homomorphism from G to some group (under function composition) of functions from S to itself. It is said that G acts on S. Many sets of transformations form a group under function composition; for example, the rotations around a point in the plane. It is often useful to consider the group as an abstract group, and to say that one has a group action of the abstract group that consists of performing the transformations of the group of transformations. The reason for distinguishing the group from the transformations is that, generally, a group of transformations of a structure acts also on various related structures; for example, the above rotation group also acts on triangles by transforming triangles into triangles. If a group acts on a structure, it will usually also act on objects built from that structure. For example, the group of Euclidean isometries acts on Euclidean space and also on the figures draw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit-stabilizer Theorem
In mathematics, a group action of a group G on a set S is a group homomorphism from G to some group (under function composition) of functions from S to itself. It is said that G acts on S. Many sets of transformations form a group under function composition; for example, the rotations around a point in the plane. It is often useful to consider the group as an abstract group, and to say that one has a group action of the abstract group that consists of performing the transformations of the group of transformations. The reason for distinguishing the group from the transformations is that, generally, a group of transformations of a structure acts also on various related structures; for example, the above rotation group also acts on triangles by transforming triangles into triangles. If a group acts on a structure, it will usually also act on objects built from that structure. For example, the group of Euclidean isometries acts on Euclidean space and also on the figures drawn i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycle Index
In combinatorial mathematics a cycle index is a polynomial in several variables which is structured in such a way that information about how a group of permutations acts on a set can be simply read off from the coefficients and exponents. This compact way of storing information in an algebraic form is frequently used in combinatorial enumeration. Each permutation π of a finite set of objects partitions that set into cycles; the cycle index monomial of π is a monomial in variables ''a''1, ''a''2, … that describes the cycle type of this partition: the exponent of ''a''''i'' is the number of cycles of π of size ''i''. The cycle index polynomial of a permutation group is the average of the cycle index monomials of its elements. The phrase cycle indicator is also sometimes used in place of ''cycle index''. Knowing the cycle index polynomial of a permutation group, one can enumerate equivalence classes due to the group's action. This is the main ingredient in the Pólya ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
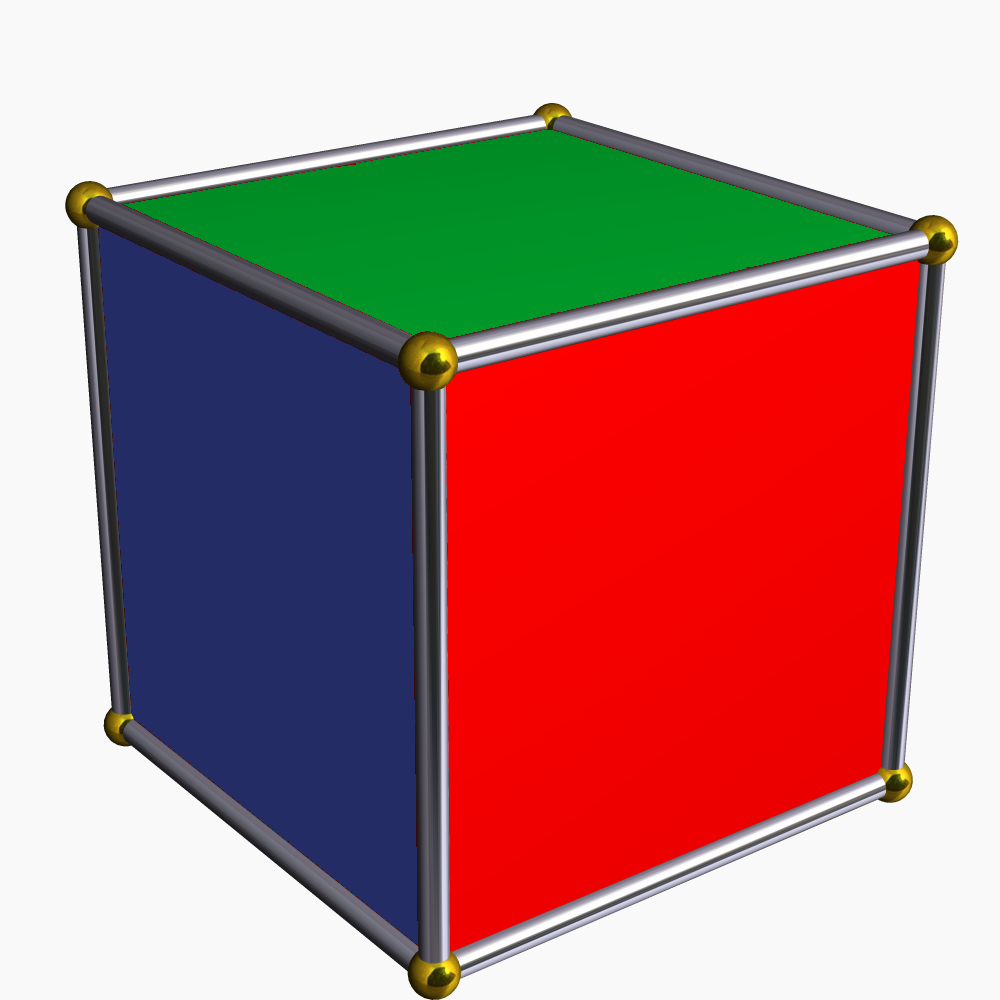
Face Colored Cube
The face is the front of the head that features the eyes, nose and mouth, and through which animals express many of their emotions. The face is crucial for human identity, and damage such as scarring or developmental deformities may affect the psyche adversely. Structure The front of the human head is called the face. It includes several distinct areas, of which the main features are: *The forehead, comprising the skin beneath the hairline, bordered laterally by the temples and inferiorly by eyebrows and ears *The eyes, sitting in the orbit and protected by eyelids and eyelashes * The distinctive human nose shape, nostrils, and nasal septum *The cheeks, covering the maxilla and mandible (or jaw), the extremity of which is the chin *The mouth, with the upper lip divided by the philtrum, sometimes revealing the teeth Facial appearance is vital for human recognition and communication. Facial muscles in humans allow expression of emotions. The face is itself a highly sensitiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Set
Fixed may refer to: * Fixed (EP), ''Fixed'' (EP), EP by Nine Inch Nails * Fixed (film), ''Fixed'' (film), an upcoming animated film directed by Genndy Tartakovsky * Fixed (typeface), a collection of monospace bitmap fonts that is distributed with the X Window System * Fixed, subjected to neutering * Fixed point (mathematics), a point that is mapped to itself by the function * Fixed line telephone, landline See also * * * Fix (other) * Fixer (other) * Fixing (other) * Fixture (other) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube (geometry)
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron. The cube can be represented in many ways, one of which is the graph known as the cubical graph. It can be constructed by using the Cartesian product of graphs. The cube is the three-dimensional hypercube, a family of polytopes also including the two-dimensional square and four-dimensional tesseract. A cube with 1, unit s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Necklace Polynomial
In combinatorial mathematics, the necklace polynomial, or Moreau's necklace-counting function, introduced by , counts the number of distinct necklaces of ''n'' colored beads chosen out of α available colors, arranged in a cycle. Unlike the usual problem of graph coloring, the necklaces are assumed to be aperiodic (not consisting of repeated subsequences), and counted up to rotation (rotating the beads around the necklace counts as the same necklace), but without flipping over (reversing the order of the beads counts as a different necklace). This counting function also describes the dimensions in a free Lie algebra and the number of irreducible polynomials over a finite field. Definition The necklace polynomials are a family of polynomials M(\alpha,n) in the variable \alpha such that :\alpha^n \ =\ \sum_ d \, M(\alpha, d). By Möbius inversion they are given by : M(\alpha,n) \ =\ \sum_\mu\!\left(\right)\alpha^d, where \mu is the classic Möbius function. A closely related fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Necklace (combinatorics)
In combinatorics, a ''k''-ary necklace of length ''n'' is an equivalence class of ''n''-character strings over an alphabet of size ''k'', taking all rotations as equivalent. It represents a structure with ''n'' circularly connected beads which have ''k'' available colors. A ''k''-ary bracelet, also referred to as a turnover (or free) necklace, is a necklace such that strings may also be equivalent under reflection. That is, given two strings, if each is the reverse of the other, they belong to the same equivalence class. For this reason, a necklace might also be called a fixed necklace to distinguish it from a turnover necklace. Formally, one may represent a necklace as an orbit of the cyclic group acting on ''n''-character strings over an alphabet of size ''k'', and a bracelet as an orbit of the dihedral group. One can count these orbits, and thus necklaces and bracelets, using Pólya's enumeration theorem. Equivalence classes Number of necklaces There are :N_k(n) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bit Vector
A bit array (also known as bitmask, bit map, bit set, bit string, or bit vector) is an array data structure that compactly stores bits. It can be used to implement a simple set data structure. A bit array is effective at exploiting bit-level parallelism in hardware to perform operations quickly. A typical bit array stores ''kw'' bits, where ''w'' is the number of bits in the unit of storage, such as a byte or word, and ''k'' is some nonnegative integer. If ''w'' does not divide the number of bits to be stored, some space is wasted due to internal fragmentation. Definition A bit array is a mapping from some domain (almost always a range of integers) to values in the set . The values can be interpreted as dark/light, absent/present, locked/unlocked, valid/invalid, et cetera. The point is that there are only two possible values, so they can be stored in one bit. As with other arrays, the access to a single bit can be managed by applying an index to the array. Assuming its size ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bijection
In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between two sets such that each element of the second set (the codomain) is the image of exactly one element of the first set (the domain). Equivalently, a bijection is a relation between two sets such that each element of either set is paired with exactly one element of the other set. A function is bijective if it is invertible; that is, a function f:X\to Y is bijective if and only if there is a function g:Y\to X, the ''inverse'' of , such that each of the two ways for composing the two functions produces an identity function: g(f(x)) = x for each x in X and f(g(y)) = y for each y in Y. For example, the ''multiplication by two'' defines a bijection from the integers to the even numbers, which has the ''division by two'' as its inverse function. A function is bijective if and only if it is both injective (or ''one-to-one'')—meaning that each element in the codomain is mappe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |