|
Bridgman's Thermodynamic Equations
In thermodynamics, Bridgman's thermodynamic equations are a basic set of thermodynamic equations, derived using a method of generating multiple thermodynamic identities involving a number of thermodynamic quantities. The equations are named after the American physicist Percy Williams Bridgman. (See also the exact differential article for general differential relationships). The extensive variables of the system are fundamental. Only the entropy ''S'' , the volume ''V'' and the four most common thermodynamic potentials will be considered. The four most common thermodynamic potentials are: : The first derivatives of the internal energy with respect to its (extensive) natural variables ''S'' and ''V'' yields the intensive parameters of the system - The pressure ''P'' and the temperature ''T'' . For a simple system in which the particle numbers are constant, the second derivatives of the thermodynamic potentials can all be expressed in terms of only ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Equations
Thermodynamics is expressed by a mathematical framework of ''thermodynamic equations'' which relate various thermodynamic quantities and physical properties measured in a laboratory or production process. Thermodynamics is based on a fundamental set of postulates, that became the laws of thermodynamics. Introduction One of the fundamental thermodynamic equations is the description of thermodynamic work in analogy to mechanical work, or weight lifted through an elevation against gravity, as defined in 1824 by French physicist Sadi Carnot. Carnot used the phrase motive power for work. In the footnotes to his famous ''On the Motive Power of Fire'', he states: “We use here the expression ''motive power'' to express the useful effect that a motor is capable of producing. This effect can always be likened to the elevation of a weight to a certain height. It has, as we know, as a measure, the product of the weight multiplied by the height to which it is raised.” With the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Temperature
Temperature is a physical quantity that expresses quantitatively the perceptions of hotness and coldness. Temperature is measured with a thermometer. Thermometers are calibrated in various temperature scales that historically have relied on various reference points and thermometric substances for definition. The most common scales are the Celsius scale with the unit symbol °C (formerly called ''centigrade''), the Fahrenheit scale (°F), and the Kelvin scale (K), the latter being used predominantly for scientific purposes. The kelvin is one of the seven base units in the International System of Units (SI). Absolute zero, i.e., zero kelvin or −273.15 °C, is the lowest point in the thermodynamic temperature scale. Experimentally, it can be approached very closely but not actually reached, as recognized in the third law of thermodynamics. It would be impossible to extract energy as heat from a body at that temperature. Temperature is important in all fields of na ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exact Differential
In multivariate calculus, a differential or differential form is said to be exact or perfect (''exact differential''), as contrasted with an inexact differential, if it is equal to the general differential dQ for some differentiable function Q in an orthogonal coordinate system. An exact differential is sometimes also called a ''total differential'', or a ''full differential'', or, in the study of differential geometry, it is termed an exact form. The integral of an exact differential over any integral path is path-independent, and this fact is used to identify state functions in thermodynamics. Overview Definition Even if we work in three dimensions here, the definitions of exact differentials for other dimensions are structurally similar to the three dimensional definition. In three dimensions, a form of the type :A(x,y,z) \,dx + B(x,y,z) \,dy + C(x,y,z) \,dz is called a differential form. This form is called ''exact'' on an open domain D \subset \mathbb^3 in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Table Of Thermodynamic Equations
This article is a summary of common equations and quantities in thermodynamics (see thermodynamic equations for more elaboration). Definitions Many of the definitions below are also used in the thermodynamics of chemical reactions. General basic quantities General derived quantities Thermal properties of matter Thermal transfer Equations The equations in this article are classified by subject. Thermodynamic processes Kinetic theory Ideal gas Entropy * S = k_\mathrm \ln \Omega , where ''k''B is the Boltzmann constant, and Ω denotes the volume of macrostate in the phase space or otherwise called thermodynamic probability. * dS = \frac , for reversible processes only Statistical physics Below are useful results from the Maxwell–Boltzmann distribution for an ideal gas, and the implications of the Entropy quantity. The distribution is valid for atoms or molecules constituting ideal gases. Corollaries of the non-relativistic Maxwell–Boltzmann ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Material Properties (thermodynamics)
The thermodynamic properties of materials are intensive thermodynamic parameters which are specific to a given material. Each is directly related to a second order differential of a thermodynamic potential. Examples for a simple 1-component system are: * Compressibility (or its inverse, the bulk modulus) :* Isothermal compressibility ::\kappa_T=-\frac\left(\frac\right)_T \quad = -\frac\,\frac :* Adiabatic compressibility ::\kappa_S=-\frac\left(\frac\right)_S \quad = -\frac\,\frac * Specific heat (Note - the extensive analog is the heat capacity) :* Specific heat at constant pressure ::c_P=\frac\left(\frac\right)_P \quad = -\frac\,\frac :* Specific heat at constant volume ::c_V=\frac\left(\frac\right)_V \quad = -\frac\,\frac * Coefficient of thermal expansion ::\alpha=\frac\left(\frac\right)_P \quad = \frac\,\frac where ''P'' is pressure, ''V'' is volume, ''T'' is temperature, ''S'' is entropy, and ''N'' is the number of particles. For a single comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compressibility
In thermodynamics and fluid mechanics, the compressibility (also known as the coefficient of compressibility or, if the temperature is held constant, the isothermal compressibility) is a measure of the instantaneous relative volume change of a fluid or solid as a response to a pressure (or mean stress) change. In its simple form, the compressibility \kappa (denoted in some fields) may be expressed as :\beta =-\frac\frac, where is volume and is pressure. The choice to define compressibility as the negative of the fraction makes compressibility positive in the (usual) case that an increase in pressure induces a reduction in volume. The reciprocal of compressibility at fixed temperature is called the isothermal bulk modulus. Definition The specification above is incomplete, because for any object or system the magnitude of the compressibility depends strongly on whether the process is isentropic or isothermal. Accordingly, isothermal compressibility is defined: :\beta_T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermal Expansion
Thermal expansion is the tendency of matter to change its shape, area, volume, and density in response to a change in temperature, usually not including phase transitions. Temperature is a monotonic function of the average molecular kinetic energy of a substance. When a substance is heated, molecules begin to vibrate and move more, usually creating more distance between themselves. Substances which contract with increasing temperature are unusual, and only occur within limited temperature ranges (see examples below). The relative expansion (also called strain) divided by the change in temperature is called the material's coefficient of linear thermal expansion and generally varies with temperature. As energy in particles increases, they start moving faster and faster weakening the intermolecular forces between them, therefore expanding the substance. Overview Predicting expansion If an equation of state is available, it can be used to predict the values of the thermal ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
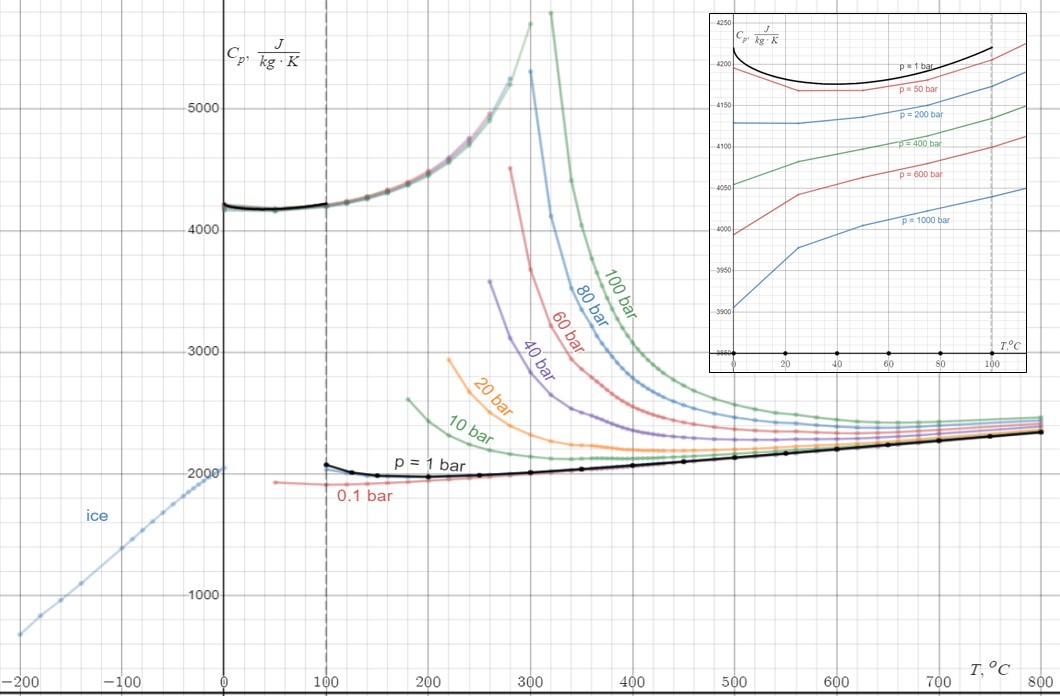
Heat Capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K). Heat capacity is an extensive property. The corresponding intensive property is the specific heat capacity, found by dividing the heat capacity of an object by its mass. Dividing the heat capacity by the amount of substance in moles yields its molar heat capacity. The volumetric heat capacity measures the heat capacity per volume. In architecture and civil engineering, the heat capacity of a building is often referred to as its thermal mass. Definition Basic definition The heat capacity of an object, denoted by C, is the limit : C = \lim_\frac, where \Delta Q is the amount of heat that must be added to the object (of mass ''M'') in order to raise its temperature by \Delta T. The value of this parameter usually varies considerably dependin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Material Properties (thermodynamics)
The thermodynamic properties of materials are intensive thermodynamic parameters which are specific to a given material. Each is directly related to a second order differential of a thermodynamic potential. Examples for a simple 1-component system are: * Compressibility (or its inverse, the bulk modulus) :* Isothermal compressibility ::\kappa_T=-\frac\left(\frac\right)_T \quad = -\frac\,\frac :* Adiabatic compressibility ::\kappa_S=-\frac\left(\frac\right)_S \quad = -\frac\,\frac * Specific heat (Note - the extensive analog is the heat capacity) :* Specific heat at constant pressure ::c_P=\frac\left(\frac\right)_P \quad = -\frac\,\frac :* Specific heat at constant volume ::c_V=\frac\left(\frac\right)_V \quad = -\frac\,\frac * Coefficient of thermal expansion ::\alpha=\frac\left(\frac\right)_P \quad = \frac\,\frac where ''P'' is pressure, ''V'' is volume, ''T'' is temperature, ''S'' is entropy, and ''N'' is the number of particles. For a single comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle Number
The particle number (or number of particles) of a thermodynamic system, conventionally indicated with the letter ''N'', is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle number is a dimensionless quantity. It is an extensive parameter, as it is directly proportional to the size of the system under consideration, and thus meaningful only for closed systems. A constituent particle is one that cannot be broken into smaller pieces at the scale of energy ''k·T'' involved in the process (where ''k'' is the Boltzmann constant and ''T'' is the temperature). For example, for a thermodynamic system consisting of a piston containing water vapour, the particle number is the number of water molecules in the system. The meaning of constituent particle, and thereby of particle number, is thus temperature-dependent. Determining the pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and even by industry. Further, both spellings are often used ''within'' a particular industry or country. Industries in British English-speaking countries typically use the "gauge" spelling. is the pressure relative to the ambient pressure. Various units are used to express pressure. Some of these derive from a unit of force divided by a unit of area; the SI unit of pressure, the pascal (Pa), for example, is one newton per square metre (N/m2); similarly, the pound-force per square inch ( psi) is the traditional unit of pressure in the imperial and U.S. customary systems. Pressure may also be expressed in terms of standard atmospheric pressure; the atmosphere (atm) is equal to this pressure, and the torr is defined as of this. Manome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamics
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of thermodynamics which convey a quantitative description using measurable macroscopic physical quantities, but may be explained in terms of microscopic constituents by statistical mechanics. Thermodynamics applies to a wide variety of topics in science and engineering, especially physical chemistry, biochemistry, chemical engineering and mechanical engineering, but also in other complex fields such as meteorology. Historically, thermodynamics developed out of a desire to increase the efficiency of early steam engines, particularly through the work of French physicist Sadi Carnot (1824) who believed that engine efficiency was the key that could help France win the Napoleonic Wars. Scots-Irish physicist Lord Kelvin was the first to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |