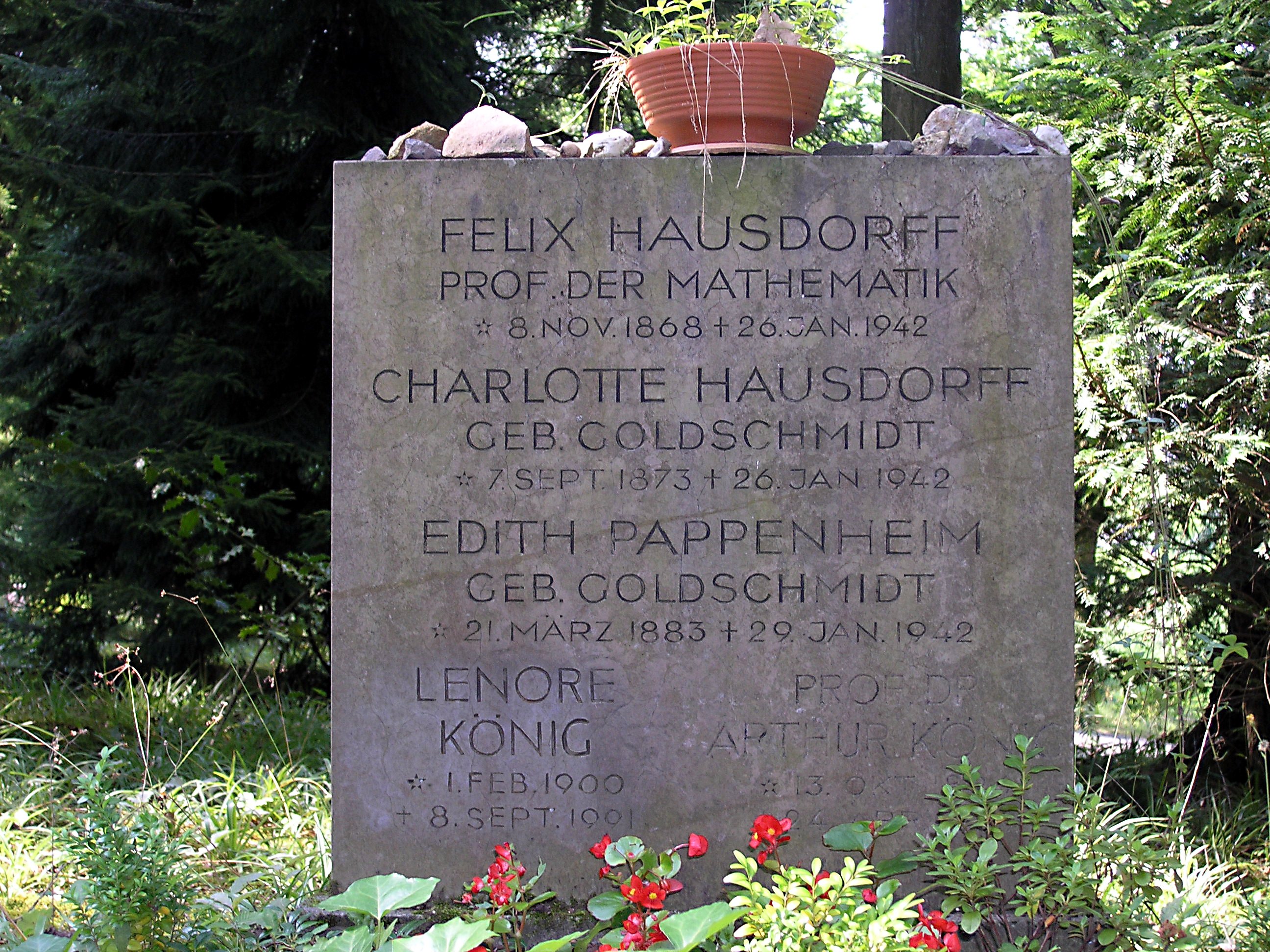|
Banach–Tarski Paradox
The Banach–Tarski paradox is a theorem in set-theoretic geometry, which states the following: Given a solid ball in three-dimensional space, there exists a decomposition of the ball into a finite number of disjoint subsets, which can then be put back together in a different way to yield two identical copies of the original ball. Indeed, the reassembly process involves only moving the pieces around and rotating them, without changing their original shape. However, the pieces themselves are not "solids" in the traditional sense, but infinite scatterings of points. The reconstruction can work with as few as five pieces. An alternative form of the theorem states that given any two "reasonable" solid objects (such as a small ball and a huge ball), the cut pieces of either one can be reassembled into the other. This is often stated informally as "a pea can be chopped up and reassembled into the Sun" and called the "pea and the Sun paradox". The theorem is a veridical paradox: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-measurable Set
In mathematics, a non-measurable set is a set which cannot be assigned a meaningful "volume". The existence of such sets is construed to provide information about the notions of length, area and volume in formal set theory. In Zermelo–Fraenkel set theory, the axiom of choice entails that non-measurable subsets of \mathbb exist. The notion of a non-measurable set has been a source of great controversy since its introduction. Historically, this led Borel and Kolmogorov to formulate probability theory on sets which are constrained to be measurable. The measurable sets on the line are iterated countable unions and intersections of intervals (called Borel sets) plus-minus null sets. These sets are rich enough to include every conceivable definition of a set that arises in standard mathematics, but they require a lot of formalism to prove that sets are measurable. In 1970, Robert M. Solovay constructed the Solovay model, which shows that it is consistent with standard set theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Countably Many
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements. In more technical terms, assuming the axiom of countable choice, a set is ''countable'' if its cardinality (the number of elements of the set) is not greater than that of the natural numbers. A countable set that is not finite is said to be countably infinite. The concept is attributed to Georg Cantor, who proved the existence of uncountable sets, that is, sets that are not countable; for example the set of the real numbers. A note on terminology Although the terms "countable" and "countably infinite" as defined he ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Congruence (geometry)
In geometry, two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other. More formally, two sets of points are called congruent if, and only if, one can be transformed into the other by an isometry, i.e., a combination of rigid motions, namely a translation, a rotation, and a reflection. This means that either object can be repositioned and reflected (but not resized) so as to coincide precisely with the other object. Therefore, two distinct plane figures on a piece of paper are congruent if they can be cut out and then matched up completely. Turning the paper over is permitted. In elementary geometry the word ''congruent'' is often used as follows. The word ''equal'' is often used in place of ''congruent'' for these objects. *Two line segments are congruent if they have the same length. *Two angles are congruent if they have the same measure. *Two circles are congruent if they have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interior (topology)
In mathematics, specifically in topology, the interior of a subset of a topological space is the union of all subsets of that are open in . A point that is in the interior of is an interior point of . The interior of is the complement of the closure of the complement of . In this sense interior and closure are dual notions. The exterior of a set is the complement of the closure of ; it consists of the points that are in neither the set nor its boundary. The interior, boundary, and exterior of a subset together partition the whole space into three blocks (or fewer when one or more of these is empty). The interior and exterior of a closed curve are a slightly different concept; see the Jordan curve theorem. Definitions Interior point If S is a subset of a Euclidean space, then x is an interior point of S if there exists an open ball centered at x which is completely contained in S. (This is illustrated in the introductory section to this article.) This definitio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bounded Set
In mathematical analysis and related areas of mathematics, a set is called bounded if all of its points are within a certain distance of each other. Conversely, a set which is not bounded is called unbounded. The word "bounded" makes no sense in a general topological space without a corresponding metric. '' Boundary'' is a distinct concept; for example, a circle (not to be confused with a disk) in isolation is a boundaryless bounded set, while the half plane is unbounded yet has a boundary. A bounded set is not necessarily a closed set and vice versa. For example, a subset of a 2-dimensional real space constrained by two parabolic curves and defined in a Cartesian coordinate system is closed by the curves but not bounded (so unbounded). Definition in the real numbers A set of real numbers is called ''bounded from above'' if there exists some real number (not necessarily in ) such that for all in . The number is called an upper bound of . The terms ''bounded from b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Felix Hausdorff
Felix Hausdorff ( , ; November 8, 1868 – January 26, 1942) was a German mathematician, pseudonym Paul Mongré (''à mogré' (Fr.) = "according to my taste"), who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, and functional analysis. Hausdorff was Jewish, and life became difficult for him and his family after the '' Kristallnacht'' of 1938. The next year he initiated efforts to emigrate to the United States, but was unable to make arrangements to receive a research fellowship. On 26 January 1942, Hausdorff, along with his wife and his sister-in-law, died by suicide by taking an overdose of veronal, rather than comply with German orders to move to the Endenich camp, and there suffer the likely implications, about which he held no illusions. Life Childhood and youth Hausdorff's father, the Jewish merchant Louis Hausdorff (1843–1896), moved with his young family to Leipzig in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1. It is often denoted ' (capital letter ). In addition to its role in real analysis, the unit interval is used to study homotopy theory in the field of topology. In the literature, the term "unit interval" is sometimes applied to the other shapes that an interval from 0 to 1 could take: , , and . However, the notation ' is most commonly reserved for the closed interval . Properties The unit interval is a complete metric space, homeomorphic to the extended real number line. As a topological space, it is compact, contractible, path connected and locally path connected. The Hilbert cube is obtained by taking a topological product of countably many copies of the unit interval. In mathematical analysis, the unit interval is a one-dimensional analytical manifold whose boundary consists of the two points 0 and 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Giuseppe Vitali
Giuseppe Vitali (26 August 1875 – 29 February 1932) was an Italian mathematician who worked in several branches of mathematical analysis. He gives his name to several entities in mathematics, most notably the Vitali set with which he was the first to give an example of a non-measurable subset of real numbers. Biography Giuseppe Vitali was the eldest of five children. His father, Domenico Vitali, worked for a railway company in Ravenna while his mother, Zenobia Casadio, was able to stay at home and look after her children. He completed his elementary education in Ravenna in 1886, and then spent three years at the Ginnasio Comunale in Ravenna where his performance in the final examinations of 1889 was average. He continued his secondary education in Ravenna at the Dante Alighieri High School. There his mathematics teacher was Giuseppe Nonni who quickly realised the young Giuseppe had great potential. He wrote to Giuseppe's father, in a letter dated 28 June 1895, asking that h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vitali Set
In mathematics, a Vitali set is an elementary example of a set of real numbers that is not Lebesgue measure, Lebesgue measurable, found by Giuseppe Vitali in 1905. The Vitali theorem is the existence theorem that there are such sets. Each Vitali set is Uncountable set, uncountable, and there are uncountably many Vitali sets. The proof of their existence depends on the axiom of choice. Measurable sets Certain sets have a definite 'length' or 'mass'. For instance, the interval (mathematics), interval [0, 1] is deemed to have length 1; more generally, an interval [''a'', ''b''], ''a'' ≤ ''b'', is deemed to have length ''b'' − ''a''. If we think of such intervals as metal rods with uniform density, they likewise have well-defined masses. The set [0, 1] ∪ [2, 3] is composed of two intervals of length one, so we take its total length to be 2. In terms of mass, we have two rods of mass 1, so the total mass is 2. There is a natural question here: if ''E'' is an arbitr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alfred Tarski
Alfred Tarski (; ; born Alfred Teitelbaum;School of Mathematics and Statistics, University of St Andrews ''School of Mathematics and Statistics, University of St Andrews''. January 14, 1901 – October 26, 1983) was a Polish-American logician and mathematician. A prolific author best known for his work on model theory, metamathematics, and algebraic logic, he also contributed to abstract algebra, topology, geometry, measure theory, mathematical logic, set theory, type theory, and analytic philosophy. Educated in Poland at the University of Warsaw, and a member of the Lwów–Warsaw school, Lwów–Warsaw school of logic and the Warsaw school of mathematics, he immigrated to the United States in 1939 where he became a naturalized citizen in 1945. Tarski taught and carried out research in mathematics at the University of California, Berkeley, from 1942 until his death in 1983.#FefA, Feferman A. His biographers Anita Burdman Feferman and Solomon Feferman state that, "Along with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stefan Banach
Stefan Banach ( ; 30 March 1892 – 31 August 1945) was a Polish mathematician who is generally considered one of the 20th century's most important and influential mathematicians. He was the founder of modern functional analysis, and an original member of the Lwów School of Mathematics. His major work was the 1932 book, ''Théorie des opérations linéaires'' (Theory of Linear Operations), the first monograph on the general theory of functional analysis. Born in Kraków to a family of Gorals, Goral descent, Banach showed a keen interest in mathematics and engaged in solving mathematical problems during school Recess (break), recess. After completing his secondary education, he befriended Hugo Steinhaus, with whom he established the Polish Mathematical Society in 1919 and later published the scientific journal ''Studia Mathematica''. In 1920, he received an assistantship at the Lwów Polytechnic, subsequently becoming a professor in 1922 and a member of the Polish Academy of Lear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |