|
Avalanche Effect
In cryptography, the avalanche effect is the desirable property of cryptographic algorithms, typically block ciphers and cryptographic hash functions, wherein if an input is changed slightly (for example, flipping a single bit), the output changes significantly (e.g., half the output bits flip). In the case of high-quality block ciphers, such a small change in either the key or the plaintext should cause a drastic change in the ciphertext. The actual term was first used by Horst Feistel, although the concept dates back to at least Shannon's ''diffusion''. If a block cipher or cryptographic hash function does not exhibit the avalanche effect to a significant degree, then it has poor randomization, and thus a cryptanalyst can make predictions about the input, being given only the output. This may be sufficient to partially or completely break the algorithm. Thus, the avalanche effect is a desirable condition from the point of view of the designer of the cryptographic algorithm or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cryptography
Cryptography, or cryptology (from "hidden, secret"; and ''graphein'', "to write", or ''-logy, -logia'', "study", respectively), is the practice and study of techniques for secure communication in the presence of Adversary (cryptography), adversarial behavior. More generally, cryptography is about constructing and analyzing Communication protocol, protocols that prevent third parties or the public from reading private messages. Modern cryptography exists at the intersection of the disciplines of mathematics, computer science, information security, electrical engineering, digital signal processing, physics, and others. Core concepts related to information security (confidentiality, data confidentiality, data integrity, authentication, and non-repudiation) are also central to cryptography. Practical applications of cryptography include electronic commerce, Smart card#EMV, chip-based payment cards, digital currencies, password, computer passwords, and military communications. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Collision Attack
In cryptography, a collision attack on a cryptographic hash tries to find two inputs producing the same hash value, i.e. a hash collision. This is in contrast to a preimage attack where a specific target hash value is specified. There are roughly two types of collision attacks: ;Classical collision attack: Find two different messages ''m''1 and ''m''2 such that ''hash''(''m''1) = ''hash''(''m''2). More generally: ;Chosen-prefix collision attack: Given two different prefixes ''p''1 and ''p''2, find two suffixes ''s''1 and ''s''2 such that ''hash''(''p''1 ∥ ''s''1) = ''hash''(''p''2 ∥ ''s''2), where ∥ denotes the concatenation operation. Classical collision attack Much like symmetric-key ciphers are vulnerable to brute force attacks, every cryptographic hash function is inherently vulnerable to collisions using a birthday attack. Due to the birthday problem, these attacks are much faster than a brute force would be. A hash of ''n'' bits can be broken in 2''n''/2 time steps (e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
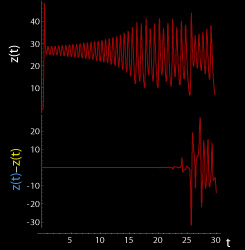
Butterfly Effect
In chaos theory, the butterfly effect is the sensitive dependence on initial conditions in which a small change in one state of a deterministic nonlinear system can result in large differences in a later state. The term is closely associated with the work of the mathematician and meteorologist Edward Norton Lorenz. He noted that the butterfly effect is derived from the example of the details of a tornado (the exact time of formation, the exact path taken) being influenced by minor perturbations such as a distant butterfly flapping its wings several weeks earlier. Lorenz originally used a seagull causing a storm but was persuaded to make it more poetic with the use of a butterfly and tornado by 1972. He discovered the effect when he observed runs of his weather model with initial condition data that were rounded in a seemingly inconsequential manner. He noted that the weather model would fail to reproduce the results of runs with the unrounded initial condition data. A very sma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Queen's University At Kingston
Queen's University at Kingston, commonly known as Queen's University or simply Queen's, is a public university, public research university in Kingston, Ontario, Kingston, Ontario, Canada. Queen's holds more than of land throughout Ontario and owns Herstmonceux Castle in East Sussex, England. Queen's is organized into eight faculties and schools. The Church of Scotland established Queen's College in October 1841 via a royal charter from Queen Victoria. The first classes, intended to prepare students for the ministry, were held 7 March 1842, with 15 students and two professors. In 1869, Queen's was the first Canadian university west of the The Maritimes, Maritime provinces to admit women. In 1883, a women's college for medical education affiliated with Queen's University was established after male staff and students reacted with hostility to the admission of women to the university's medical classes. In 1912, Queen's ended its affiliation with the Presbyterian Church, and adopted ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bent Function
In the mathematical field of combinatorics, a bent function is a Boolean function that is maximally non-linear; it is as different as possible from the set of all linear and affine functions when measured by Hamming distance between truth tables. Concretely, this means the maximum correlation between the output of the function and a linear function is minimal. In addition, the derivatives of a bent function are balanced Boolean functions, so for any change in the input variables there is a 50 percent chance that the output value will change. The maximal nonlinearity means approximating a bent function by an affine (linear) function is hard, a useful property in the defence against linear cryptanalysis. In addition, detecting a change in the output of the function yields no information about what change occurred in the inputs, making the function immune to differential cryptanalysis. Bent functions were defined and named in the 1960s by Oscar Rothaus in research not published ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Completeness (cryptography)
In cryptography, a boolean function is said to be complete if the value of each output bit depends on ''all'' input bits. This is a desirable property to have in an encryption cipher, so that if one bit of the input ( plaintext) is changed, every bit of the output (ciphertext) has an average of 50% probability Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an e ... of changing. The easiest way to show why this is good is the following: consider that if we changed our 8-byte plaintext's last byte, it would only have any effect on the 8th byte of the ciphertext. This would mean that if the attacker guessed 256 different plaintext-ciphertext pairs, he would always know the last byte of every 8byte sequence we send (effectively 12.5% of all our data). Finding out 256 plaintext-ciphertext pair ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signed Number Representations
In computing, signed number representations are required to encode negative numbers in binary number systems. In mathematics, negative numbers in any base are represented by prefixing them with a minus sign ("−"). However, in RAM or CPU registers, numbers are represented only as sequences of bits, without extra symbols. The four best-known methods of extending the binary numeral system to represent signed numbers are: sign–magnitude, ones' complement, two's complement, and offset binary. Some of the alternative methods use implicit instead of explicit signs, such as negative binary, using the base −2. Corresponding methods can be devised for other bases, whether positive, negative, fractional, or other elaborations on such themes. There is no definitive criterion by which any of the representations is universally superior. For integers, the representation used in most current computing devices is two's complement, although the Unisys ClearPath Dorado series mainf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Product Cipher
In cryptography, a product cipher combines two or more transformations in a manner intending that the resulting cipher is more secure than the individual components to make it resistant to cryptanalysis.Handbook of Applied Cryptography by Alfred J. Menezes, Paul C. van Oorschot, Scott A. Vanstone. Fifth Printing (August 2001) page 251. The product cipher combines a sequence of simple transformations such as substitution (S-box), permutation (P-box), and modular arithmetic. The concept of product ciphers is due to Claude Shannon, who presented the idea in his foundational paper, ''Communication Theory of Secrecy Systems''. A particular product cipher design where all the constituting transformation functions have the same structure is called an iterative cipher with the term " rounds" applied to the functions themselves. For transformation involving reasonable number of n message symbols, both of the foregoing cipher systems (the S-box and P-box) are by themselves wanting. Shannon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Butterfly Effect
In chaos theory, the butterfly effect is the sensitive dependence on initial conditions in which a small change in one state of a deterministic nonlinear system can result in large differences in a later state. The term is closely associated with the work of the mathematician and meteorologist Edward Norton Lorenz. He noted that the butterfly effect is derived from the example of the details of a tornado (the exact time of formation, the exact path taken) being influenced by minor perturbations such as a distant butterfly flapping its wings several weeks earlier. Lorenz originally used a seagull causing a storm but was persuaded to make it more poetic with the use of a butterfly and tornado by 1972. He discovered the effect when he observed runs of his weather model with initial condition data that were rounded in a seemingly inconsequential manner. He noted that the weather model would fail to reproduce the results of runs with the unrounded initial condition data. A very sma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Preimage Attack
In cryptography, a preimage attack on cryptographic hash functions tries to find a message that has a specific hash value. A cryptographic hash function should resist attacks on its preimage (set of possible inputs). In the context of attack, there are two types of preimage resistance: * ''preimage resistance'': for essentially all pre-specified outputs, it is computationally infeasible to find any input that hashes to that output; i.e., given , it is difficult to find an such that . * ''second-preimage resistance'': for a specified input, it is computationally infeasible to find another input which produces the same output; i.e., given , it is difficult to find a second input such that . These can be compared with a collision resistance, in which it is computationally infeasible to find any two distinct inputs , that hash to the same output; i.e., such that . Collision resistance implies second-preimage resistance. Second-preimage resistance implies preimage resistance only ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Length Extension Attack
In cryptography and computer security, a length extension attack is a type of attack where an attacker can use Hash(''message1'') and the length of ''message1'' to calculate Hash(''message1'' ‖ ''message2'') for an attacker-controlled ''message2'', without needing to know the content of ''message1''. This is problematic when the hash is used as a message authentication code with construction Hash(''secret'' ‖ ''message''), and ''message'' and the length of ''secret'' is known, because an attacker can include extra information at the end of the message and produce a valid hash without knowing the secret. Algorithms like MD5, SHA-1 and most of SHA-2 that are based on the Merkle–Damgård construction are susceptible to this kind of attack. Truncated versions of SHA-2, including SHA-384 and SHA-512/256 are not susceptible, nor is the SHA-3 algorithm. HMAC In cryptography, an HMAC (sometimes expanded as either keyed-hash message authentication code or hash-based messag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cryptanalyst
Cryptanalysis (from the Greek ''kryptós'', "hidden", and ''analýein'', "to analyze") refers to the process of analyzing information systems in order to understand hidden aspects of the systems. Cryptanalysis is used to breach cryptographic security systems and gain access to the contents of encrypted messages, even if the cryptographic key is unknown. In addition to mathematical analysis of cryptographic algorithms, cryptanalysis includes the study of side-channel attacks that do not target weaknesses in the cryptographic algorithms themselves, but instead exploit weaknesses in their implementation. Even though the goal has been the same, the methods and techniques of cryptanalysis have changed drastically through the history of cryptography, adapting to increasing cryptographic complexity, ranging from the pen-and-paper methods of the past, through machines like the British Bombes and Colossus computers at Bletchley Park in World War II, to the mathematically advanced ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |