|
Armstrong's Axioms
Armstrong's axioms are a set of axioms (or, more precisely, inference rules) used to infer all the functional dependencies on a relational database. They were developed by William W. Armstrong in his 1974 paper. The axioms are sound in generating only functional dependencies in the closure of a set of functional dependencies (denoted as F^) when applied to that set (denoted as F). They are also complete in that repeated application of these rules will generate all functional dependencies in the closure F^+. More formally, let \langle R(U), F \rangle denote a relational scheme over the set of attributes U with a set of functional dependencies F. We say that a functional dependency f is logically implied by F, and denote it with F \models f if and only if for every instance r of R that satisfies the functional dependencies in F, r also satisfies f. We denote by F^ the set of all functional dependencies that are logically implied by F. Furthermore, with respect to a set of inferen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or fit' or 'that which commends itself as evident'. The precise definition varies across fields of study. In classic philosophy, an axiom is a statement that is so evident or well-established, that it is accepted without controversy or question. In modern logic, an axiom is a premise or starting point for reasoning. In mathematics, an ''axiom'' may be a " logical axiom" or a " non-logical axiom". Logical axioms are taken to be true within the system of logic they define and are often shown in symbolic form (e.g., (''A'' and ''B'') implies ''A''), while non-logical axioms are substantive assertions about the elements of the domain of a specific mathematical theory, for example ''a'' + 0 = ''a'' in integer arithmetic. N ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inference Rule
Rules of inference are ways of deriving conclusions from premises. They are integral parts of formal logic, serving as norms of the logical structure of valid arguments. If an argument with true premises follows a rule of inference then the conclusion cannot be false. ''Modus ponens'', an influential rule of inference, connects two premises of the form "if P then Q" and "P" to the conclusion "Q", as in the argument "If it rains, then the ground is wet. It rains. Therefore, the ground is wet." There are many other rules of inference for different patterns of valid arguments, such as ''modus tollens'', disjunctive syllogism, constructive dilemma, and existential generalization. Rules of inference include rules of implication, which operate only in one direction from premises to conclusions, and rules of replacement, which state that two expressions are equivalent and can be freely swapped. Rules of inference contrast with formal fallaciesinvalid argument forms involving logi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Dependency
In relational database theory, a functional dependency is the following constraint between two attribute sets in a relation: Given a relation ''R'' and attribute sets ''X'',''Y'' \subseteq ''R'', ''X'' is said to functionally determine ''Y'' (written ''X'' → ''Y'') if each ''X'' value is associated with precisely one ''Y'' value. ''R'' is then said to satisfy the functional dependency ''X'' → ''Y''. Equivalently, the projection \Pi_R is a function, that is, ''Y'' is a function of ''X''. In simple words, if the values for the ''X'' attributes are known (say they are ''x''), then the values for the ''Y'' attributes corresponding to ''x'' can be determined by looking them up in ''any'' tuple of ''R'' containing ''x''. Customarily ''X'' is called the ''determinant'' set and ''Y'' the ''dependent'' set. A functional dependency FD: ''X'' → ''Y'' is called ''trivial'' if ''Y'' is a subset of ''X''. In other words, a dependency FD: ''X'' → ''Y'' means that the values of ''Y'' ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
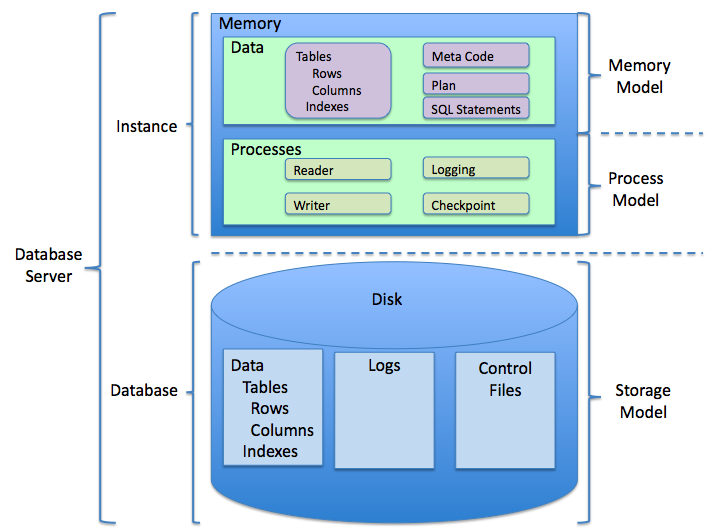
Relational Database
A relational database (RDB) is a database based on the relational model of data, as proposed by E. F. Codd in 1970. A Relational Database Management System (RDBMS) is a type of database management system that stores data in a structured format using rows and columns. Many relational database systems are equipped with the option of using SQL (Structured Query Language) for querying and updating the database. History The concept of relational database was defined by E. F. Codd at IBM in 1970. Codd introduced the term ''relational'' in his research paper "A Relational Model of Data for Large Shared Data Banks". In this paper and later papers, he defined what he meant by ''relation''. One well-known definition of what constitutes a relational database system is composed of Codd's 12 rules. However, no commercial implementations of the relational model conform to all of Codd's rules, so the term has gradually come to describe a broader class of database systems, which at a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Ward Armstrong
William Ward Armstrong is a Canadian mathematician and computer scientist. He earned his Ph.D. from the University of British Columbia in 1966 and is most known as the originator Armstrong's axioms of dependency in a Relational database A relational database (RDB) is a database based on the relational model of data, as proposed by E. F. Codd in 1970. A Relational Database Management System (RDBMS) is a type of database management system that stores data in a structured for .... Works * William W. Armstrong, Yatsuka Nakamura, Piotr Rudnicki, "Armstrong's Axioms", Formalized Mathematics V. 11 No. 1, pp. 39 – 51, University of Bialystok, 2003. * Guoliang Qu, John R. Feddes, Richard N. Coleman, William W. Armstrong, Jerry L. Leonard, Method and Apparatus for estimating odor concentration using an electronic nose, US patent 6,411,905 B1, June 25, 2002. * W. W. Armstrong, D. O. Gorodnichy, Breaking Hyperplanes to fit Data with Applications to 3D World Modeling and Oil Sand ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soundness
In logic and deductive reasoning, an argument is sound if it is both Validity (logic), valid in form and has no false premises. Soundness has a related meaning in mathematical logic, wherein a Formal system, formal system of logic is sound if and only if every well-formed formula that can be proven in the system is logically valid with respect to the Semantics of logic, logical semantics of the system. Definition In deductive reasoning, a sound argument is an argument that is Validity (logic), valid and all of its premises are true (and as a consequence its conclusion is true as well). An argument is valid if, assuming its premises are true, the conclusion ''must be'' true. An example of a sound argument is the following well-known syllogism: : ''(premises)'' : All men are mortal. : Socrates is a man. : ''(conclusion)'' : Therefore, Socrates is mortal. Because of the logical necessity of the conclusion, this argument is valid; and because the argument is valid and its premises ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closure (mathematics)
In mathematics, a subset of a given set (mathematics), set is closed under an Operation (mathematics), operation on the larger set if performing that operation on members of the subset always produces a member of that subset. For example, the natural numbers are closed under addition, but not under subtraction: is not a natural number, although both 1 and 2 are. Similarly, a subset is said to be closed under a ''collection'' of operations if it is closed under each of the operations individually. The closure of a subset is the result of a closure operator applied to the subset. The ''closure'' of a subset under some operations is the smallest superset that is closed under these operations. It is often called the ''span'' (for example linear span) or the ''generated set''. Definitions Let be a set (mathematics), set equipped with one or several methods for producing elements of from other elements of .Operation (mathematics), Operations and (partial function, partial) multivar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Completeness (logic)
In mathematical logic and metalogic, a formal system is called complete with respect to a particular property if every formula having the property can be derived using that system, i.e. is one of its theorems; otherwise the system is said to be incomplete. The term "complete" is also used without qualification, with differing meanings depending on the context, mostly referring to the property of semantical validity. Intuitively, a system is called complete in this particular sense, if it can derive every formula that is true. Other properties related to completeness The property converse to completeness is called soundness: a system is sound with respect to a property (mostly semantical validity) if each of its theorems has that property. Forms of completeness Expressive completeness A formal language is ''expressively complete'' if it can express the subject matter for which it is intended. Functional completeness A set of logical connectives associated with a formal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Database Theory
Database theory encapsulates a broad range of topics related to the study and research of the theoretical realm of databases and database management systems. Theoretical aspects of data management include, among other areas, the foundations of query languages, Computational complexity theory, computational complexity and expressive power (computer science), expressive power of queries, finite model theory, database design theory, dependency theory (database theory), dependency theory, foundations of concurrency control and database recovery, deductive databases, temporal database, temporal and spatial databases, real-time databases, managing uncertain data and probabilistic databases, and Web data. Most research work has traditionally been based on the relational model, since this model is usually considered the simplest and most foundational model of interest. Corresponding results for other data models, such as object-oriented or semi-structured models, or, more recently, graph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Modeling
Data modeling in software engineering is the process of creating a data model for an information system by applying certain formal techniques. It may be applied as part of broader Model-driven engineering (MDE) concept. Overview Data modeling is a process used to define and analyze data requirements needed to support the business processes within the scope of corresponding information systems in organizations. Therefore, the process of data modeling involves professional data modelers working closely with business stakeholders, as well as potential users of the information system. There are three different types of data models produced while progressing from requirements to the actual database to be used for the information system.Simison, Graeme. C. & Witt, Graham. C. (2005). ''Data Modeling Essentials''. 3rd Edition. Morgan Kaufmann Publishers. The data requirements are initially recorded as a conceptual data model which is essentially a set of technology independent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |